非对称通道内亲疏水结构影响下的纳米气泡滑移效应

戴双武，卢艳，高友明，李扬帆

非对称通道内亲疏水结构影响下的纳米气泡滑移效应

戴双武，卢艳，高友明，李扬帆

（武汉科技大学 a.冶金装备及其控制教育部重点实验室 b.武汉科技大学机械传动与制造工程湖北省重点实验室，武汉 430081）

研究非对称性通道中亲疏水表面结构影响下纳米气泡特征与边界滑移之间的关系，以实现良好的流体减阻效果。采用二元体系分子动力学方法，研究纳米气泡在通道流动中产生的滑移减阻效应。首先建立上下壁面非对称微通道模型，通过考虑微通道流动传热过程，探究纳米气泡影响下的微通道界面速度滑移现象。保持亲水下壁面高度以及上下壁面温差不变的情况下，增加上壁面纳米结构高度，对通道中纳米气泡体积产生促进作用。另外，当上壁面为疏水壁面时，气泡呈现为壁面形式，并且随着体积增大，相对应通道中上壁面滑移长度增大；当上壁面为亲水壁面时，纳米气泡呈现为体相形式，并且随着体积增大，对应上壁面滑移长度减小。非对称性通道内，在上壁面结构高度影响下，壁面形式的气泡体积增大对通道内减阻具有促进作用，而体相形式的气泡体积增大对通道内减阻具有抑制作用。

微通道；温度阶跃；速度滑移；纳米气泡；滑移减阻；润湿性

近年来，随着科技的发展，微纳科学已经应用到了各个工程领域[1-4]。当热流体流过纳米通道时，通道内的能量传递和物质运输都会在受限制的微小尺度空间内进行，因此纳米通道的固液界面会产生与宏观尺度不同的现象，宏观尺度固液界面的理论不再适用。因为在宏观尺度下，表面效应对通道固液界面流体流动性的影响较小，并且宏观通道流体流动性的研究都是基于无边界滑移情况下进行的，而微纳尺度通道中，表面效应则不可忽视，而且会影响到整个通道中流体的流动性[5-7]。研究发现，由于表面效应作用，流体流过微通道固体壁面时，会存在速度滑移[8]，且具有一定的界面速度滑移长度[9]。Zhang等人[10-11]对纳米通道中流体的研究发现，固体壁面的润湿性会影响流体运动，并发现固液相互作用力较差时，界面会出现比较明显的速度滑移。Voronov等[12]利用分子动力学方法研究纳米通道中的流体行为时，发现固液界面的滑移长度与固体表面的润湿性相关，对于润湿性较差的固体表面，滑移长度会随润湿性的降低而增加。曹炳阳等人[13]通过研究通道中流体滑移现象发现，固体壁面的表面势能越强，界面速度滑移长度越小。表面润湿性不同，固液界面可能发生负滑移、无滑移以及正滑移等不同现象。另外，固体表面粗糙度大小也能影响固液之间的润湿性变化[14-15]。Pit等[16]研究发现，固体表面粗糙度能够影响固体表面的速度滑移。Choi等[17]在研究牛顿流体的减阻机理时发现，固体表面粗糙度可以使界面滑移长度增大，结构变化会影响粗糙度的变化，进而影响滑移长度。张程宾等人[18]利用仿真方法对比光滑以及粗糙固体表面流体的流动发现，粗糙结构的存在限制了流体的运动，导致固液界面速度滑移长度减小。Ou等人[19]通过合理设计疏水固体表面的结构尺寸来探讨固体表面的减阻性能时发现，对比光滑表面，疏水表面微结构的存在，使得界面速度滑移长度较大。Rahmatipour等[20]利用分子动力学方法对粗糙通道进行研究时发现，纳米结构高度越高，壁面滑移长度越长。其次，研究表明，当流体流过粗糙固体表面时，将会有气体滞留在微织构内部，并在其表面形成稳定的气泡，从而使固液之间产生滑移减阻效应[21-22]。Elias等人[23-24]在研究通道中流体的运动时发现，气泡的产生是实现通道固体表面滑移减阻的关键因素。

温度也是影响纳米通道中气泡成核的因素之一[25]。Lin等人[26-27]通过微通道中加热丝加热流体时发现，只有当微通道中液体温度接近临界温度时，才会有热气泡产生。Yang等[28]研究结果表明，升高疏水表面的温度，在表面粗糙的地方更易形成纳米气泡。张雪花等[29]在研究固体表面上已经形成的纳米气泡时发现，当液体温度升高到某个定值时，纳米气泡体积达到最大，然后随温度的升高而减小。刘桦等[30]发现，固体表面温度影响了通道中流体滑移减阻。

综上所述，关于纳米通道中流体的滑移减阻已有大量研究，大部分是考虑纳米气泡影响下对称性管道中的流体运动，且关于温度对纳米气泡的研究也都处于实验阶段。然而，非对称性管道的应用却十分广泛[31-32]，因此研究非对称通道内纳米气泡的滑移减阻效应具有重要意义。目前，通过调整非对称通道的微结构来改变通道表面粗糙度和流体温度，从而影响纳米气泡特性的通道减阻理论研究并不完善。本文首先采用分子动力学模型，主要研究了非对称性通道内上壁面结构高度影响下纳米气泡与流体流动之间的关系，通过控制上下壁面温差、润湿性，并保持下壁面结构高度不变，探讨了改变疏水或者亲水上壁面结构高度，通道中纳米气泡体积的变化情况。然后，进一步研究了纳米气泡体积与通道中界面滑移长度之间的关系。

1 微通道流体传热仿真模型

本文采用分子动力学（MD）模拟方法，利用开源程序LAMMPS仿真软件来研究纳米通道内纳米气泡成核体积与壁面能量传递之间的关系。非对称模型通道如图1所示。

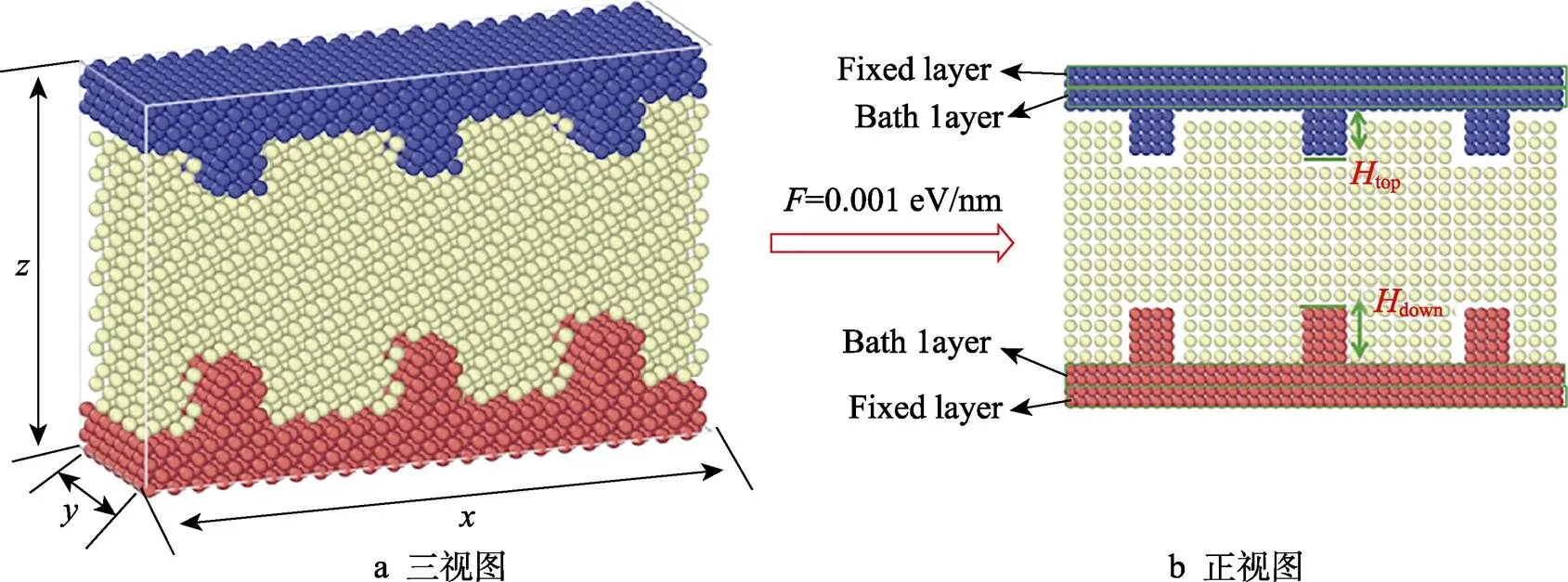
图1 非对称通道模型

图1a为非对称纳米通道三视图，模拟微通道在、和方向上的尺寸分别为9、2.6、6 nm。二维模型（图1b）中，上壁面蓝色粒子为疏水性铂原子，下壁面红色粒子为亲水性铂原子，中间黄色粒子为流体氩原子。流体氩原子被限制在两个平行的铂固体壁面之间，固体和液体原子的初始状态都是面心立方体FCC晶格排列（固体粒子的晶格常数为0.392 nm，流体粒子的晶格常数为0.543 nm）。为了提高模型的真实性和保持系统的稳定性，和方向设为周期性边界，方向设为固定边界。

图1b为非对称通道模型的正视图，固体壁面分为内外两层，外层被固定，以保持系统的稳定性（壁面外两层原子标记为固定层），内层为浴热层（下壁面内两层原子为高温浴热层，上壁面内两层原子为低温浴热层）。上壁面包括上壁面固定层、低温浴热层、结构，定义为top；下壁面包括下壁面固定层、高温浴热层、结构，定义为down。下壁面结构高度定义为down，上壁面结构高度定义为top。本文通过改变亲疏水壁面结构高度参数（top）来展开通道减阻研究。另外，液体由2100个氩原子组成，上下固体壁面大约2800个铂原子。Lennard-Jones（LJ）势能描述了粒子之间的相互作用力，见式(1)。

设置势函数的截止距离=0.85 nm，仿真系统的时间步长为0.01 ps。首先采用速度校定法将整个系统NVE驰豫，经过2 ps达到平衡状态。接着对系统浴热，用NVT（粒子数恒定，体积、温度保持不变）对上、下固体壁面进行控温，将上壁面温度top控制在86 K，下壁面温度down控制在100 K，同时对液体施加一个方向的恒定驱动力（驱=0.001 eV/nm），并将系统加热时间由2 ps延长到9 ps，以达到平衡状态。最后对整个系统进行切片，并统计数据。

表1 原子之间的相互作用力势能参数及其作用距离[34]

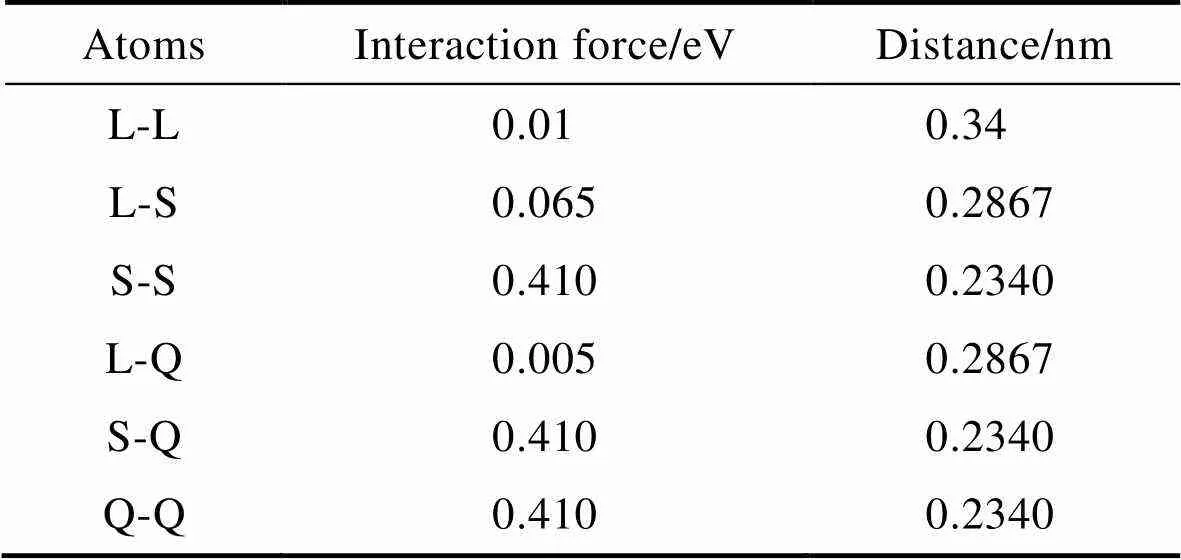
Tab.1 Potential parameters and interaction distancesof interaction force between atoms[34]

2 疏水壁面结构高度影响下的纳米气泡

2.1 纳米气泡成核

保持down=1 nm、top=86 K、down=100 K不变，改变疏水上壁面的结构高度（0～0.8 nm）时，上壁面纳米气泡的成核规律如图2所示。可以看出，上壁面的高度由0 nm增大到0.8 nm时，近下壁面附近的流体被吸附，气泡在近上壁面区域出现，并且上壁面附近流体中纳米气泡的体积越来越大。这是因为疏水性表面结构高度增加，壁面疏水性增强，使得上壁面的气泡成核体积增大。

2.2 通道流体密度分布

改变结构高度，对流体中气泡的形成有明显影响，致使流体密度的分布有差异。为了研究通道中仅疏水上壁面结构高度变化时，通道中纳米气泡与流体密度之间的关系，将模型进行切层，统计密度。待系统粒子分布均匀后，再对系统进行切层处理，并将模型分为70层。

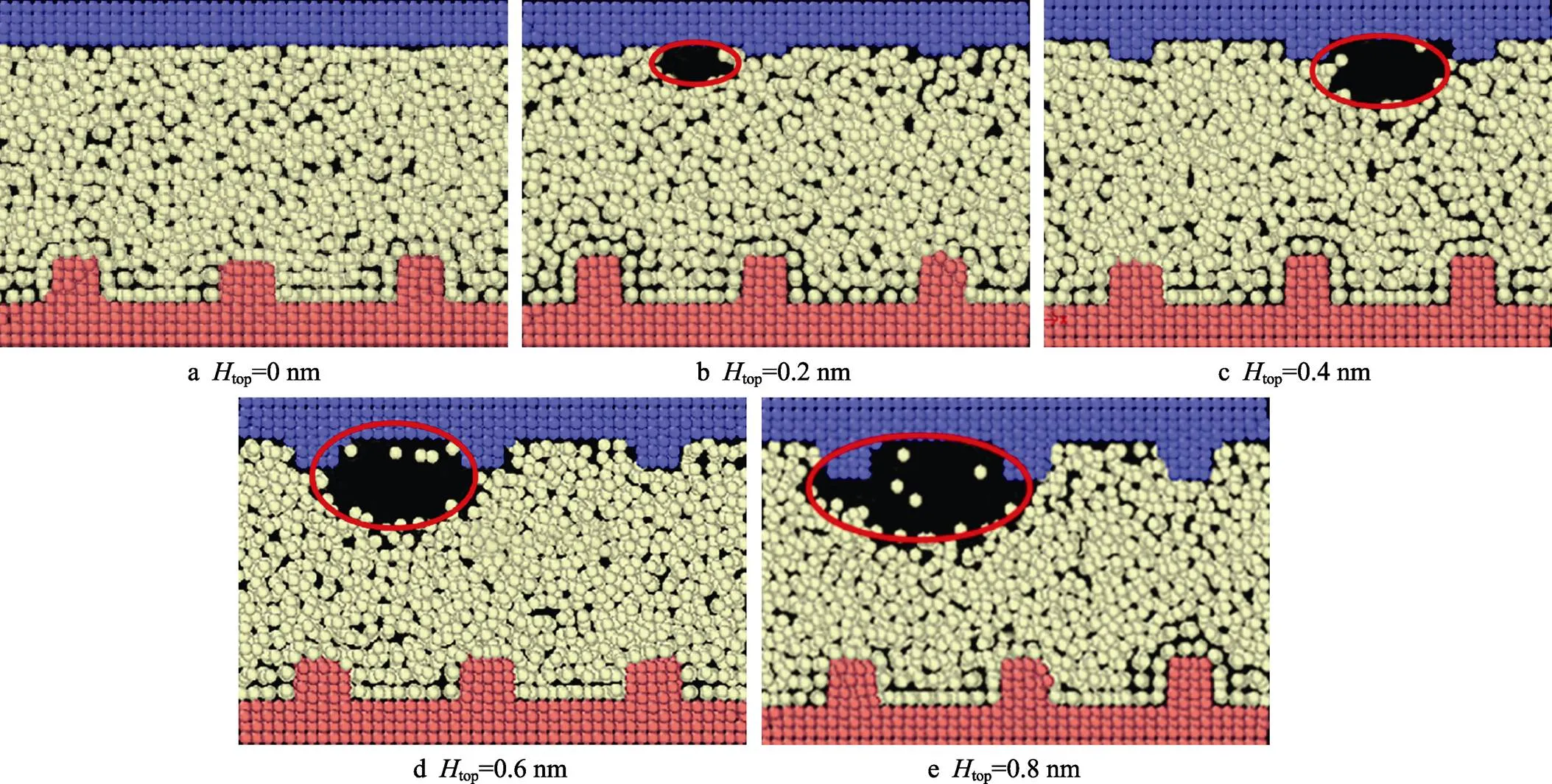
图2 上壁面结构高度影响下的气泡成核

通道中流体密度沿方向的分布如图3所示。由于体系中液体与固体粒子之间的势能作用域为纳米级别，因此固体壁面只影响近壁面流体区域的密度分布特性。由图3可知，由于固体表面效应，近壁面流体区域密度分布出现振荡现象。在通道中心主流区域，流体粒子受固体粒子的影响较小，密度几乎不发生变化。由于上下壁面的润湿性不同，以及上下壁面结构不对称，所以通道内流体密度呈不对称分布。当down=1 nm、top=86 K、down=100 K时，通过改变上壁面的结构高度，来分析流体密度的分布规律。结果发现，上壁面结构高度增加，近下壁面区域流体分布基本不变，近上壁面区域流体密度呈近乎直线的下降趋势。这是由于增加上壁面结构高度，近上壁面区域流体中纳米气泡成核体积变大。

图3 疏水上壁面结构高度影响下流体沿z方向的密度分布

2.3 疏水界面气泡影响下微通道流体的流动性

通道内壁结构高度变化会影响流体中纳米气泡的生成，导致流体密度分布发生变化，从而影响通道中流体的流动传热。为了研究仅通道上壁面结构高度变化时，纳米气泡体积与流体速度分布之间的关系，取3组数据进行分析。当top=86 K、down=100 K、down=1 nm时，改变上壁面结构高度，通道中流体的速度分布如图4所示。结果显示，在通道的中心区域，流体速度整体呈不对称分布。在上壁面结构高度变化影响下，近上下壁面区域的流体速度、流体平均速度和纳米气泡体积见表2。可以分析得出，随着上壁面结构高度的增加，上壁面纳米气泡体积变大，近上下壁面的流体速度正向增大，通道流体平均速度变大。这是由于上壁面流体中气泡成核体积增大，减小了下壁面固液接触面积，使得流体与固体之间的运动阻力降低。

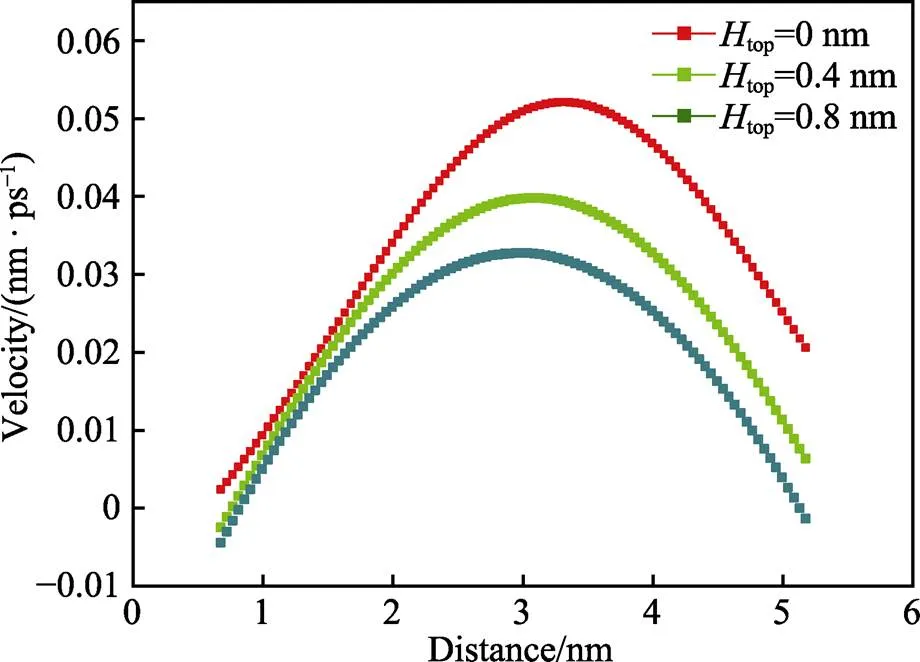
图4 纳米气泡影响下流体沿z方向的速度分布

表2 不同疏水上壁面高度影响下近上下壁面区域流体速度与板面的速度差、流体平均速度大小和纳米气泡体积

Tab.2 Difference between the velocity of the fluid near the upper and lower walls and the velocity of the platesurface, the average velocity of the fluid and the volume of the nanobubbles on different height of drain upper wall

2.4 气泡影响下流体温度分布

在恒定外力驱动下，流体在纳米通道中流动时，流体粒子之间、流体粒子与粗糙固体表面之间都会存在摩擦，致使流体温度变化，进而影响纳米气泡的变化。为了讨论改变疏水上壁面结构高度变化时，纳米气泡体积与流体温度分布之间的关系，采用类似的模型处理方式，选取具有代表性的几组数据进行分析。当top=86 K、down=100 K、down=1 nm时，改变上壁面结构高度，流体温度的分布状况如图5所示。可以看到，增加上壁面结构高度，通道中流体温度的平均水平下降。在上下壁面温度以及下壁面结构高度不变时，改变上壁面结构高度，通道中近上下壁面的流体温差、平均流体温度和纳米气泡体积见表3。结合表3与图5分析可以得到，随着上壁面结构高度的增加，上壁面气泡体积增大，对应近上下壁面流体温差以及流体平均温度都呈正向减小的趋势。其原因是，疏水上壁面结构高度增加，一方面促进了通道中的传热，流体温度降低；另一方面，增大了壁面疏水性，壁面气泡体积增大。

图5 纳米气泡影响下流体沿z方向的温度分布

表3 不同疏水上壁面高度影响下近上下壁面流体温度差、流体平均温度、纳米气泡的体积

Tab.3 Fluid temperature difference near the upper and lower walls, average fluid temperature, volume of nanobubbles on different height of drain upper wall

3 亲水上壁面结构高度影响下的纳米气泡

3.1 上壁面结构高度对气泡成核影响

模拟中，模型处理与第2节一样，仅将上壁面的疏水性铂壁面换为亲水性铂壁面。将模型运行至系统能量平衡后，输出并记录仿真结果。在top=86 K、down=100 K、down=1 nm下，改变亲水上壁面结构高度时，微通道流体中纳米气泡的成核规律如图6所示。从图6中可以看出，top为0、0.2、0.4、0.6、0.8 nm时，气泡成核出现在微通道主流区域，并且随着上壁面结构高度的增加，通道流体中纳米气泡体积越来越大。这是由于上壁面的结构高度增加，使得壁面对流体粒子的吸引面积增大，通道中央流体出现密度不均匀的现象越来越明显，因而气泡越来越大。

3.2 气泡影响下通道流体密度分布

通过在模型方向施加恒定力，保持流体运动，同时改变上壁面结构高度，通道中气泡的生成就会发生变化，那么通道中粒子分布也会发生改变。为了研究仅亲水上壁面结构高度变化时，通道中气泡与流体密度之间的关系，将模型进行切层，统计密度，待系统粒子分布均匀后，再对系统进行切层处理。当top=86 K、down=100 K、down=1 nm时，改变上壁面结构高度，通道中流体密度的分布如图7所示。可以看出，当上壁面为亲水壁面时，近壁面区域流体密度同样存在震荡现象，通道中央出现密度减小的现象。上下壁面的结构不对称，使得通道流体密度分布不对称。上壁面高度越高时，相对应近上壁面区域流体密度波动越明显。这是由于亲水上壁面结构高度增加，增大了近上壁面区域流体与亲水铂结构之间的接触面积。另外，上壁面结构较高的通道内，通道中央流体密度大幅度减小。这是因为上壁面结构高度增加，通道中央气泡的成核体积变大。

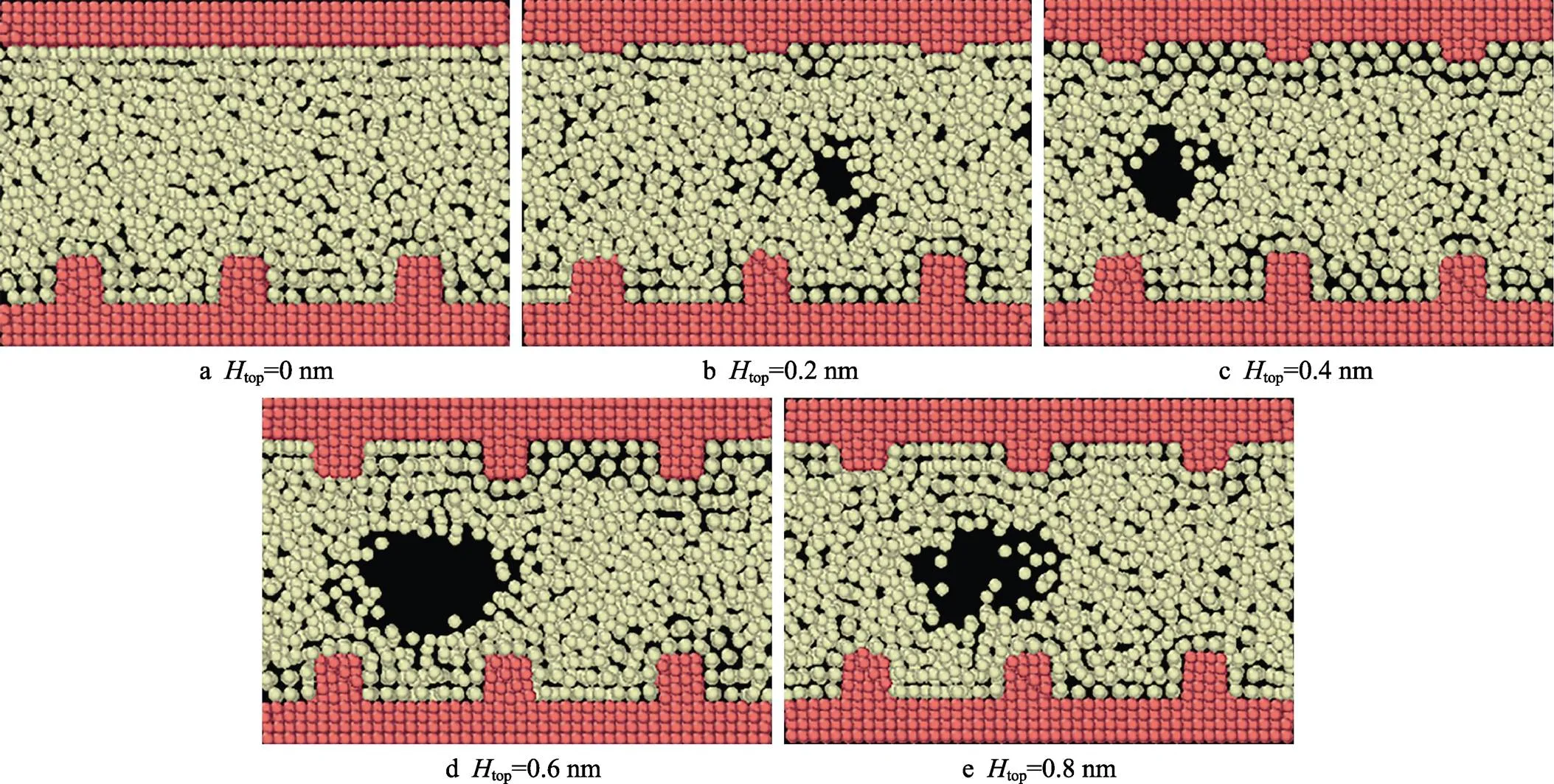
图6 亲水上壁面结构高度变化影响下的纳米气泡

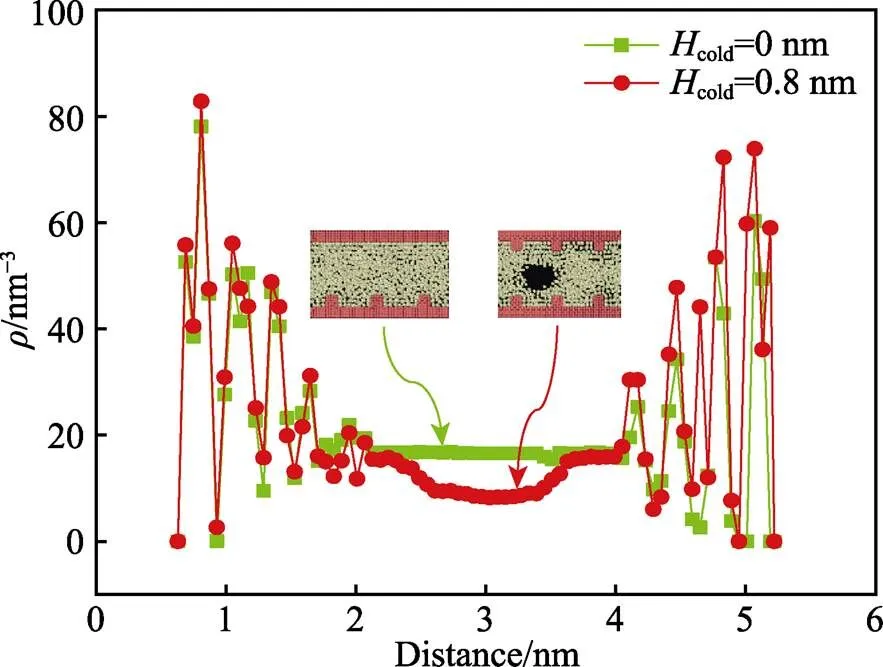
图7 纳米气泡影响下的流体沿z方向的密度分布

3.3 气泡影响下通道流体的流动性

当气泡形成形式发生改变时，流体密度分布发生突变，粒子间接触形式发生改变，通道中的动量传递也会发生变化。在top=86 K、down=100 K、down=1 nm时，改变亲水上壁面结构高度，通道中的流体速度分布如图8所示。可以看到，速度整体呈不对称分布，并且上壁面高度增加，通道中流体平均速度降低。这是由于亲水上壁面结构高度增加，增大了固体壁面对流体粒子的吸附能力，干扰了流体运动。当上下壁面温差以及下壁面纳米结构高度不变时，在上壁面结构高度变化的影响下，近上下壁面区域的流体速度、通道流体平均速度和纳米气泡体积见表4。可以看出，随着上壁面结构高度的增加，通道中央纳米气泡体积不断变大，近上下壁面区域流体速度正向减小，流体平均速度也不断变小。这是由于通道流体中纳米气泡的成核体积增大，阻碍了流体流动所致。

图8 纳米结构高度影响下流体沿z方向的速度分布

3.4 气泡影响下通道温度分布

流体的密度分布以及粒子间的动量传递发生变化，流体与流体的黏性摩擦就会发生改变，通道中流体温度也会发生变化。当top=86 K、down=100 K、down=1 nm时，改变上壁面结构高度，流体温度的分布状况如图9所示。可以看到，增加上壁面结构高度，通道中流体的平均温度下降。这是因为壁面结构高度增加，流体粒子与固体壁面的接触面积增加，传热效率增大。在上下壁面温度以及下壁面结构高度不变时，改变上壁面结构高度，通道中近上下壁面的流体温差、流体平均温度和纳米气泡体积见表5。结合表5与图9分析可得，随着上壁面纳米结构高度的增加，通道流体中纳米气泡体积增大，对应近上下壁面流体温差及流体平均温度都呈正向减小趋势。这是因为亲水上壁面结构高增加，壁面的润湿性增大，通道中气泡的成核体积增大。同时，结构高度增加，流体粒子的吸附面积增大，通道中界面的传热效率提高。

表4 不同亲水上壁面高度影响下近上下壁面流体速度与板面的速度差、流体平均速度大小和纳米气泡体积

Tab.4 Difference between the velocity of the fluid near the upper and lower walls and the velocity of plate surface, average fluid velocity and the volume of the nanobubble on different hydrophilic upper wall height

图9 上壁面结构高度影响下流体沿z方向的温度分布

表5 不同亲水上壁面高度影响下近上下壁面流体温度差、流体平均温度、纳米气泡体积

Tab.5 Relationship between fluid temperature difference near the upper and lower walls, the average fluid temperature, and the volume of the nanobubble on different hydrophilic upper wall height

4 气泡影响下流体中滑移

改变通道中结构高度，纳米气泡体积大小和流体密度、速度、温度分布就会发生变化，界面能量传导也会发生变化。对于疏水表面气泡影响下滑移长度与表面结构粗糙度的关系，本文对比了文献[35]的结果（如图10所示），实验与仿真所得结果的变化规律一致，但存在差异。这是由于本文仿真通道中固液界面传热的存在，以及文献采用的表面材料等不同。

为了探究亲、疏水上壁面结构高度变化影响下，通道中纳米气泡体积与界面速度滑移之间的关系，将所有数据进行统计，并按照式(2)计算速度滑移长度。

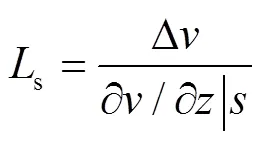
式中：Δv为近固体壁下的液体速度；为流体在固液界面下的速度梯度。

当top=86 K、down=100 K、down=1 nm时，改变下壁面结构高度，通道中纳米气泡体积与上下壁面速度滑移之间的关系如图11所示。由图11可知，保持下壁面结构高度不变，当上壁面为疏水壁面时，增加上壁面结构高度，上壁面附近流体中气泡的体积增大，上壁面的速度滑移长度增大。这是由于壁面纳米气泡的存在，降低了上壁面固液之间的接触面积，动量传递效率提高。当上壁面为亲水壁面时，增加上壁面结构高度，上壁面速度滑移的长度减小。这是因为通道中央纳米体积越大，对通道中流体流动的阻碍越强。

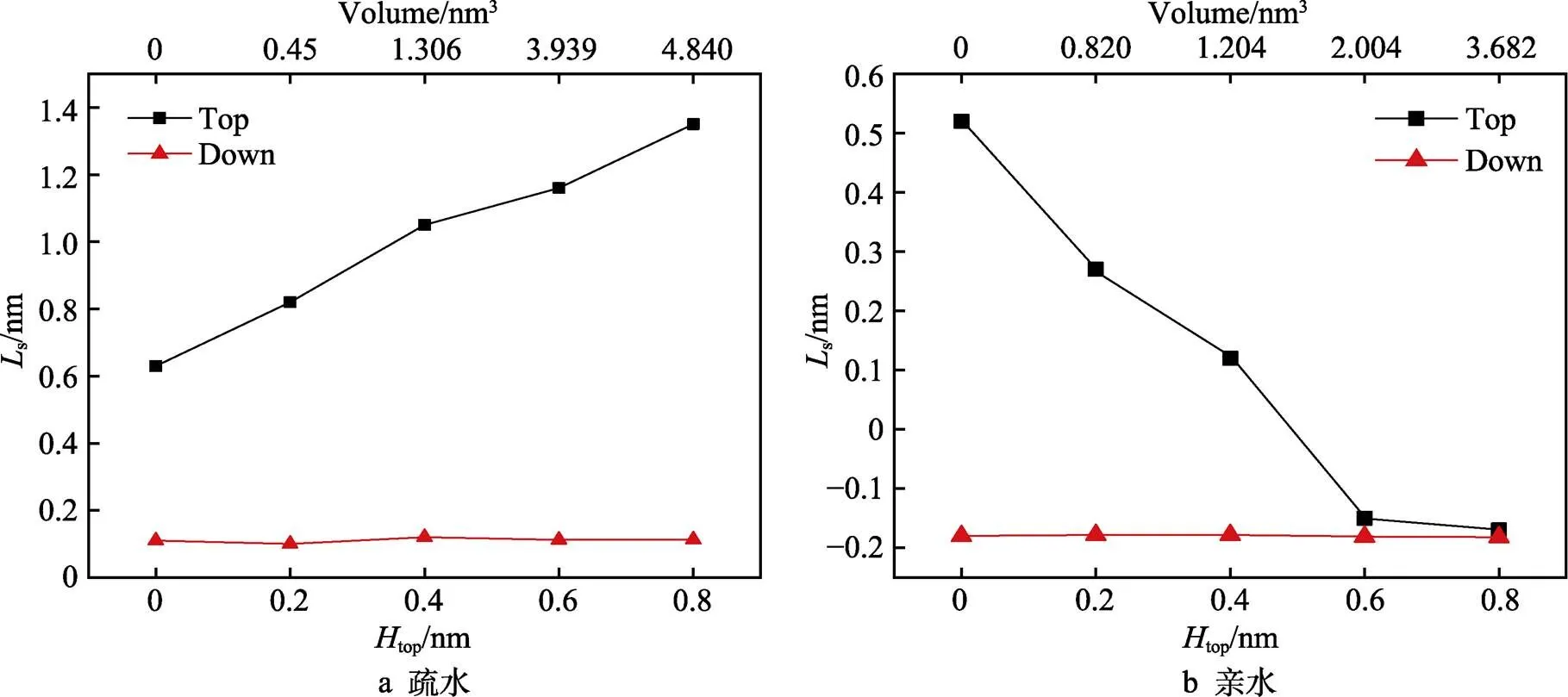
图11 不同壁面结构高度影响下气泡体积与速度滑移的关系

5 结论

本文使用MD模拟研究了非对称纳米通道内，上壁面为亲、疏水壁面影响下纳米气泡成核体积的大小，然后进一步探索了通道中纳米气泡与界面滑移行为之间的关系，得出以下结论：

1）非对称通道中，当保持下壁面结构高度以及上下壁面温差不变时，增加上壁面结构高度，通道中流体的平均温度下降，纳米气泡的体积增大。

2）非对称通道内，当保持下壁面结构高度以及上下壁面温差不变，上壁面为疏水壁面时，纳米气泡呈壁面形式，且疏水壁面附近纳米气泡体积的增大，对应上壁面的速度滑移长度正向增大，而下壁面的速度滑移长度不变，通道中流体运动阻力变小。

3）非对称通道内，当保持下壁面结构高度以及上下壁面温差不变，上壁面为亲水壁面时，纳米气泡呈体相形式，通道中纳米气泡体积增大，上壁面的速度滑移长度减小，而下壁面的速度滑移长度不变，通道中流体运动阻力增大。

[1] ZHANG Guang, XU Yan-tong, DUAN Zheng, et al. Enh­an­cement of Evaporative Heat Transfer on Carbon Nano­tube Sponges by Electric Field Reinforced Wettability[J]. Applied Surface Science, 2018, 454: 262-269.

[2] CHOI S M, JANG S H, LEE Dong hun, et al. Spray Chara­cteristics of the Rotating Fuel Injection System of a Micro-Jet Engine[J]. Journal of Mechanical Science and Technology, 2010, 24(2): 551-558.

[3] SOHRABI S, LIU Ya-ling. Modeling Thermal Inkjet and Cell Printing Process Using Modified Pseudopotential and Thermal Lattice Boltzmann Methods[J]. Physical Review E, 2018, 97(3-1): 033105.

[4] ALTINTAS Z, AKGUN M, KOKTURK G, et al. A Fully Automated Microfluidic-Based Electrochemical Sensor for Real-Time Bacteria Detection[J]. Biosensors and Bioelec­tronics, 2018, 100: 541-548.

[5] 黄桥高, 潘光, 宋保维. 疏水表面滑移流动及减阻特性的格子Boltzmann方法模拟[J]. 物理学报, 2014, 63(5): 236-242.

HUANG Qiao-gao, PAN Guang, SONG Bao-wei. Lattice Boltzmann Simulation of Slip Flow and Drag Reduction Characteristics of Hydrophobic Surfaces[J]. Acta Physica Sinica, 2014, 63(5): 236-242.

[6] 葛宋, 陈民. 接触角与液固界面热阻关系的分子动力学模拟[J]. 物理学报, 2013, 62(11): 110204.

GE Song, CHEN Min. A Molecular Dynamics Simulation on the Relationship between Contact Angle and Solid- Liquid Interfacial Thermal Resistance[J]. Acta Physica Sinica, 2013, 62(11): 110204.

[7] 顾骁坤, 陈民. 纳米硅通道内滑移现象的分子动力学模拟[J]. 工程热物理学报, 2010, 31(10): 1724-1726.

GU Xiao-kun, CHEN Min. Molecular Dynamics Simula­tions of the Slip Phenomena in Silicon Nano-channels[J]. Journal of Engineering Thermophysics, 2010, 31(10): 1724-1726.

[8] JOSEPH P, TABELING P. Direct Measurement of the Apparent Slip Length[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2005, 71(3 Pt 2A): 035303.

[9] HUANG Qiao-gao, PAN Guang, SONG Bao-wei, et al. Lattice Boltzmann Simulation of Slip Flow and Drag Re­duction Characteristics of Hydrophobic Surfaces[J]. Acta Physica Sinica, 2014, 63(5): 054701.

[10] NAGAYAMA G, CHENG Ping. Effects of Interface Wet­tability on Microscale Flow by Molecular Dynamics Sim­ulation[J]. International Journal of Heat and Mass Tran­sfer, 2004, 47(3): 501-513.

[11] ZHANG Hong-wu, ZHANG Zhong-qiang, YE Hong-fei. Molecular Dynamics-based Prediction of Boundary Slip of Fluids in Nanochannels[J]. Microfluidics and Nanoflui­dics, 2012, 12(1-4): 107-115.

[12] VORONOV R S, PAPAVASSILIOU D V, LEE L L. Slip Length and Contact Angle over Hydrophobic Surfaces[J]. Chemical Physics Letters, 2007, 441(4-6): 273-276.

[13] 曹炳阳, 陈民, 过增元. 纳米通道内液体流动的滑移现象[J]. 物理学报, 2006, 55(10): 5305-5310.

CAO Bing-yang, CHEN Min, GUO Zeng-yuan. Velocity Slip of Liquid Flow in Nanochannels[J]. Acta Physica Sinica, 2006, 55(10): 5305-5310.

[14] 王甜. 固着纳米水滴润湿行为的分子动力学模拟[D]. 大连: 大连理工大学, 2015.

WANG Tian. Wetting Behaviors of Sessile Water Nano- Droplets Using Molecular Dynamics Simulation[D]. Da­lian: Dalian University of Technology, 2015.

[15] MARMUR A, BITTOUN E. When Wenzel and Cassie are Right: Reconciling Local and Global Considerations[J]. Langmuir: The ACS Journal of Surfaces and Colloids, 2009, 25(3): 1277-1281.

[16] PIT R, HERVET H, LÉGER L. Direct Experimental Evi­d­ence of Slip in Hexadecane: Solid Interfaces[J]. Physical Review Letters, 2000, 85(5): 980-983.

[17] CHOI C H, ULMANELLA U, KIM J, et al. Effective Slip and Friction Reduction in Nanograted Superhydrophobic Microchannels[J]. Physics of Fluids, 2006, 18(8): 087105.

[18] 张程宾, 许兆林, 陈永平. 粗糙纳通道内流体流动与传热的分子动力学模拟研究[J]. 物理学报, 2014, 63(21): 263-270.

ZHANG Cheng-bin, XU Zhao-lin, CHEN Yong-ping. Mo­­lecular Dynamics Simulation on Fluid Flow and Heat Transfer in Rough Nano Channels[J]. Acta Physica Sinica, 2014, 63(21): 263-270.

[19] OU Jia, PEROT B, ROTHSTEIN J P. Laminar Drag Red­u­ction in Microchannels Using Ultrahydrophobic Surfa­ces[J]. Physics of Fluids, 2004, 16(12): 4635-4643.

[20] RAHMATIPOUR H, AZIMIAN A. Molecular Dynamics Simulation of Couette Flow Behavior in Smooth and Ro­ugh Nanochannels[J]. Physica A, 2015, 15(7): 119-130.

[21] LUM K, CHANDLER D, WEEKS J D. Hydrophobicity at Small and Large Length Scales[J]. The Journal of Phy­sical Chemistry B, 1999, 103(22): 4570-4577.

[22] OU Jia, PEROT B, ROTHSTEIN J P. Laminar Drag Re­duction in Microchannels Using Ultrahydrophobic Sur­faces[J]. Physics of Fluids, 2004, 16(12): 4635-4643.

[23] ALJALLIS E, SARSHAR M A, DATLA R, et al. Exper­imental Study of Skin Friction Drag Reduction on Super­h­y­drophobic Flat Plates in High Reynolds Number Boun­dary Layer Flow[J]. Physics of Fluids, 2013, 25(2): 025103.

[24] JAGDISH B N, XIAN BRANDON T Z, KWEE T J, et al. Experimental Study of Air Layer Sustainability for Frict­ional Drag Reduction[J]. Journal of Ship Research, 2014, 58(1): 30-42.

[25] LOHSE D, ZHANG Xue-hua. Pinning and Gas Oversatu­ration Imply Stable Single Surface Nanobubbles[J]. Phy­sical Review E, Statistical, Nonlinear, and Soft Matter Ph­y­sics, 2015, 91(3): 031003.

[26] LIN Li-wei. Microscale Thermal Bubble Formation: The­r­m­ophysical Phenomena and Applications[J]. Microscale Thermophysical Engineering, 1998, 2(2): 71-85.

[27] LIN L, UDELL K S, PISANO A P. Liquid-V Apor Phase Transition and Bubble Formation in Micro Structures[J]. Thermal science engineering, 1994, 2(1): 52-59.

[28] YANG Shang-jiong, DAMMER S M, BREMOND N, et al.Characterization of Nanobubbles on Hydrophobic Surfaces in Water[J]. Langmuir: The ACS Journal of Surfaces and Colloids, 2007, 23(13): 7072-7077.

[29] ZHANG X H, LI G, WU Z H, et al. Effect of Temperature on the Morphology of Nanobubbles at Mica/Water Inter­face[J]. Chinese Physics B, 2005, 14(9): 1774-1778.

[30] 刘桦, 孙仁. 控温、系统温度和外载荷对纳米通道中水流性质的影响[J]. 水动力学研究与进展, 2020, 35(6): 719-725.

LIU Hua, SUN Ren. Effects of Temperature Control, Sys­tem Temperature and External Load on Properties of Water Flow Inside Nanochannel[J]. Chinese Journal of Hydro­d­y­na­mics, 2020, 35(6): 719-725.

[31] CHEN Qin-wen, MENG Ling-yi, LI Qi-kai, et al. Water Transport and Purification in Nanochannels Controlled by Asymmetric Wettability[J]. Small, 2011, 7(15): 2225-2231.

[32] DE GANS B J, KITA R, MÜLLER B, et al. Negative Thermodiffusion of Polymers and Colloids in Solvent Mixtures[J]. The Journal of Chemical Physics, 2003, 118(17): 8073-8081.

[33] 张龙艳. 微尺度下流体的流动换热及核化沸腾的分子动力学研究[D]. 北京: 华北电力大学(北京), 2019.

ZHANG Long-yan. Molecular Dynamics Simulation of Fluid Flow and Heat Transfer and Nucleate Boiling in Microscale[D]. Beijing: North China Electric Power Uni­versity, 2019.

[34] 王艳红. 润湿性对纳米尺度薄液膜爆炸沸腾现象影响的分子动力学模拟[D]. 北京: 华北电力大学(北京), 2018.

WANG Yan-hong. Molecular Dynamics Simulations of the Effect of Wettability on Explosive Boiling of a Nan­oscale Thin Liquid Film[D]. Beijing: North China Electric Power University, 2018.

[35] 李大勇. 固液界面纳米气泡及其对流体边界滑移影响的研究[D]. 哈尔滨: 哈尔滨工业大学, 2014.

LI Da-yong. Study of Nanobubbles at Solid-Liquid Inter­face and the Influence of Nanobubbles on Boundary Slip of Fluids[D]. Harbin: Harbin Institute of Technology, 2014.

Slip Effect of Nanobubbles under the Influence of Hydrophilic and Hydrophobic Structures in Asymmetric Channels

,,,

(a. Key Laboratory of Metallurgical Equipment and Control Technology of Ministry of Education, b. Key Laboratory of Mechanical Transmission and Manufacturing Engineering, Wuhan University of Science and Technology, Wuhan 430081, China)

The purpose of this paper is to achieve a good fluid drag reduction effect by studying the relationship between the characteristics of nanobubbles and boundary slip under the influence of hydrophilic and hydrophobic surface structures in asymmetric channels. In this paper, the binary system molecular dynamics method is used to study the slip drag reduction effect of nanobubbles flowing in the channel. Firstly, the asymmetric microchannel model on the upper and lower walls is established, and the microchannel interface velocity slip phenomenon under the influence of nanobubbles is explored by considering the flow and heat transfer process of the microchannel. The simulation results show that when keeping the height of the hydrophilic lower wall and the temperature difference between the upper and lower walls unchanged, the increase in the height of the nanostructures on the upper wall promotes the volume increase of nanobubbles in the channel; in addition, when the upper wall is a hydrophobic wall, the nanobubbles appear in the form of a wall surface. As the volume increases, the slip length of the upper wall in the corresponding channel increases; when the upper wall is a hydrophilic wall, the nanobubbles are in bulk form, and as the volume increases, the corresponding upper wall’s slip length is reduced. In an asymmetrical channel, under the influence of the height of the upper wall structure, the increase of the nanobubble volume in the form of a wall surface promotes the drag reduction in the channel, while the increase of the nanobubble volume in the bulk form inhibits the drag reduction in the channel. Therefore, the research results in this paper provide a theoretical basis for exploring the application of nanobubble engineering in drag reduction.

microchannel; temperature step; velocity slip; nanobubbles; slip drag reduction; wettability

TH117

A

1001-3660(2022)02-0202-09

10.16490/j.cnki.issn.1001-3660.2022.02.019

2021-03-16；

2021-07-05

2021-03-16；

2021-07-05

国家自然科学基金（51875417，51975425）

The National Natural Science Foundation of China (51875417, 51975425)

戴双武（1995—），男，硕士研究生，主要研究方向为摩擦学理论。

DAI Shuang-wu (1995—), Male, Postgraduate, Research focus: tribological theories.

卢艳（1984—），女，博士，副教授，主要研究方向为表面摩擦学理论。

LU Yan (1984—), Female, Doctor, Associate professor, Research focus: surface tribology theory.

戴双武, 卢艳, 高友明, 等.非对称通道内亲疏水结构影响下的纳米气泡滑移效应[J]. 表面技术, 2022, 51(2): 202-210.

DAI Shuang-wu, LU Yan, GAO You-ming, et al. Slip Effect of Nanobubbles under the Influence of Hydrophilic and Hydrophobic Structures in Asymmetric Channels[J]. Surface Technology, 2022, 51(2): 202-210.