壁面函数在超声速湍流模拟中的应用

王新光,毛枚良,何琨,*,陈琦,万钊

1. 中国空气动力研究与发展中心 计算空气动力研究所,绵阳 621000 2. 中国空气动力研究与发展中心 空气动力学国家重点实验室,绵阳 621010

湍流数值模拟是当前计算流体力学(CFD)的核心问题之一,在现有高速大存储计算机资源的支持下,涌现了大批关于直接数值模拟和大涡模拟的相关湍流研究成果,但对于复杂工程外形的湍流模拟,目前仍只能采用计算资源消耗较小的RANS方法。众所周知,对于工程中常用的SST-模型,如需精确模拟壁面摩阻和热流,通常要求在壁面网格密度满足≈1,所需计算机资源往往难以满足工程应用对效率的要求。为此,主流商业软件中通常采用壁面函数,耦合不同的湍流模型来进行湍流模拟。

壁面函数从理论研究角度来看,是边界层方程的近似解,其最初形式为对数律,刻画了零压力梯度不可压附体边界层流动的速度分布,之后得到了考虑压力梯度和零剪应力情况下边界层方程的渐近解,文献[2-4]都相继对标准壁面函数进行了修正研究。其中Nichols发展了流动可压缩性和热传导的壁面函数,并将其应用到可压缩湍流平板的数值求解中,贺旭照等将其与-两方程模型耦合应用到可压缩拐角的数值求解中。另外国内吴晓军和肖红林等分别在RANS模拟和大涡模拟简单二维流动中采用壁面函数,Gao和Tao等分别通过数值实验和风洞试验对壁面函数的系数进行了壁面函数修正研究。但壁面函数在压力梯度不可忽略的区域内是否仍然有效尚无定论,对于存在分离和再附的复杂流动依然存在困难。

文献[15]通过DNS总结壁面附近湍流黏性系数分布,解析求解湍流边界层方程,从而获得壁面网格内的解析速度和温度分布,称为解析壁面函数,并将其推广到可压缩流动,通过简单流动验证了解析壁面函数对于在分离流动中具有良好的表现。

另一方面壁面函数仅作用于壁面网格,与全局流动的湍流模型存在不相容的问题,容易引起数值模拟结果对壁面附近第一层网格节点位置的强烈依赖性,使得数值预测的分离和再附区域精度变差。Tidriri和Knopp等将计算区域划分为近壁区域和整体区域,在近壁区域通过子迭代的方式求解壁面剪切应力,在固壁面上始终满足原始边界条件,在近壁区域的外缘和整体RANS数值求解匹配一致。Kalitzin等通过不可压缩平板边界层数值计算,建立了摩擦速度和壁面第一个点的雷诺数之间的关系数据表,求解摩擦来得到壁面剪切应力,从而数值实现壁面函数在其不可压缩笛卡尔RANS求解器中的应用。

目前大多数壁面函数研究主要基于平板边界层,而工程实际的飞行器表面,通常是三维曲面,这使得一些复杂的壁面函数在实际应用中容易出现数值刚性的问题,该方法对于工程复杂外形的推广应用仍有一定距离,这也是在一些复杂流动的模拟中又重新回归到一些简单的壁面函数的原因。

本文基于国家数值风洞气动力计算平台, 针对工程湍流模型SST-,开展适用的壁面函数研究,给出了具体的程序实现过程和边界处理形式,通过典型二维算例完成了壁面函数模块考核,最后基于内外流一体化的超声速飞行器湍流流动的模拟,完成了模块对复杂外流的工程应用考核。

1 壁面函数

对于充分发展的湍流边界层,基于所谓的双层模型,分为黏性底层和对数率层,如图1所示。

黏性底层是一个紧贴固体壁面的极薄层,分子黏性切应力是主要特征因素,湍流切应力极小且可以忽略,所以流动似乎处于层流状态,沿壁面法向呈线性分布,其区域为<。对数率层是一个距壁面较远的流体层,流动处于完全湍流状态,湍流涡黏性远大于分子黏性,速度分布接近于对数率,位于从>到0.2倍边界层厚度范围内,在局部平衡的湍流边界层内,可通过理论推导得到标准壁面函数,其具体形式为

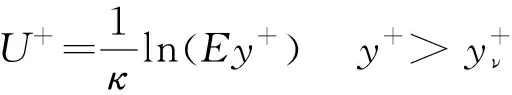
(1)

(2)

式中:

=()12=

(3)

=()12=

(4)

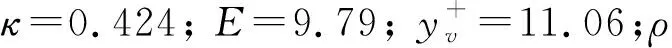
图1 湍流边界层示意图Fig.1 Sketch map of turbulence boundary layer

2 壁面函数在三维边界层中的推广应用

从平面推广到三维曲面,就是把边界层方程及其相关理论表达式转换到贴体坐标系中,如图2 所示。以当地离开壁面第1个计算单元处的切向速度作为流动方向,将三维流动进行局部二维化处理,在此基础上采用湍流边界层的壁面函数,得到壁面剪切应力。

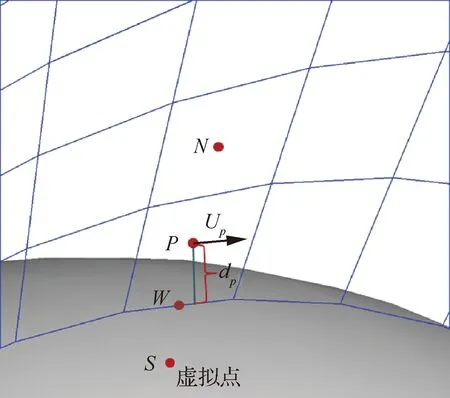
图2 三维壁面网格示意图Fig.2 Sketch map of three-dimentional near-wall mesh

为了尽可能减少对源程序的修改,通过引入壁面虚拟湍流涡黏性系数来实现壁面函数,根据摩擦速度的定义,可以得到壁面剪切应力为

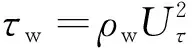
(5)

根据壁面剪切应力的定义：

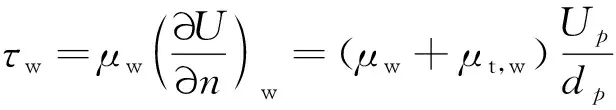
(6)

式中:为壁面湍流黏性系数；和为邻近壁面计算单元的切向速度和壁面距离,如图2所示。根据式(5)、式(6)可以得到壁面湍流黏性系数为

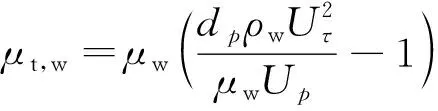
(7)

基于国家数值风洞(NNW)软件平台,将SST-两方程湍流模型和壁面函数模块进行了耦合。NNW软件平台的基础算法为有限体积方法,其中黏性项采用二阶精度中心型格式离散,对流项采用二阶TVD(Total Variation Diminishing)型格式,时间项采用LU-SGS隐式迭代算法。为了适应复杂外形,采用了分区网格算法。壁面边界采用虚拟点方法实现,因此,通过修正虚拟点(如图2中点)的值,来达到修正壁面剪切应力的目的。虚拟点湍流黏性系数为

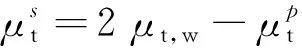
(8)

以上标准壁面函数确定的虚拟点湍流黏性系数没有涉及到具体的湍流模型,实际上,对边界上湍流变量也需要进行适当的处理。壁面湍动能耗散率在黏性底层对数率层分别为

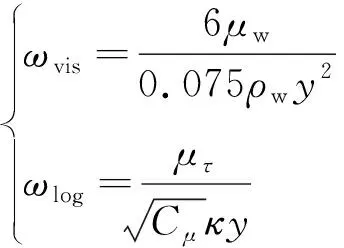
(9)

式中:涡黏性常数=0.09。

对于SST-两方程湍流模型,壁面网格点上的湍流输运变量可相应求出,其中

(10)

壁面虚拟点的湍流输运变量为

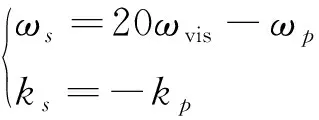
(11)

求解SST-两方程湍流模型的RANS方程时,结合以上描述的标准壁面函数,规定当>11.06时采用壁面函数边界条件,当≤11.06时,SST-两方程湍流模型直接作用到壁面。由于摩擦速度与壁面剪切应力相互耦合,利用壁面函数不能显式求得计算等量,需要采用迭代方式,具体过程如图3所示。

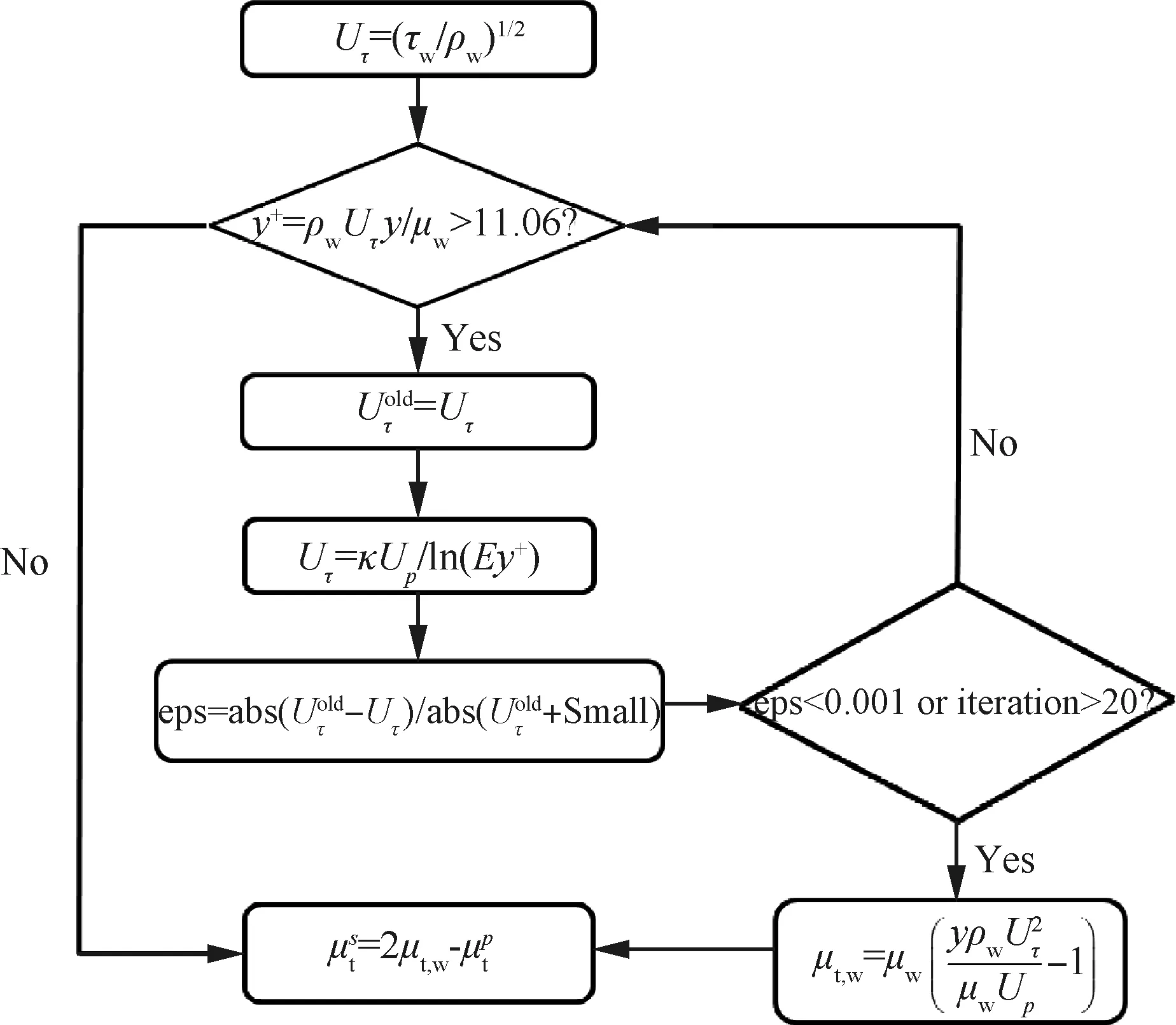
图3 壁面函数程序实现流程图Fig.3 Flow chart of wall function method in code

3 算例与分析

3.1 压缩拐角

本算例用于考察壁面函数对湍流边界层和分离流动的预测结果精度的影响规律。压缩拐角来流马赫数为2.85,来流压力为23 600 N/m,来流温度为100.3 K,等温壁为276 K,湍流边界层厚度=2.3 cm,压缩拐角=24°。

图4为计算采用的网格,为了能够精确捕捉拐角处的激波边界层干扰,对网格拐角处进行了加密,在拐角处网格流向距离为0.1 mm,整体规模为201×51(流向×法向),壁面距离分别取0.001 mm、0.01 mm、0.1 mm和1 mm,其中密网格=0.001 mm,分离区之前≈0.1,粗网格=1 mm,分离区之前≈200。

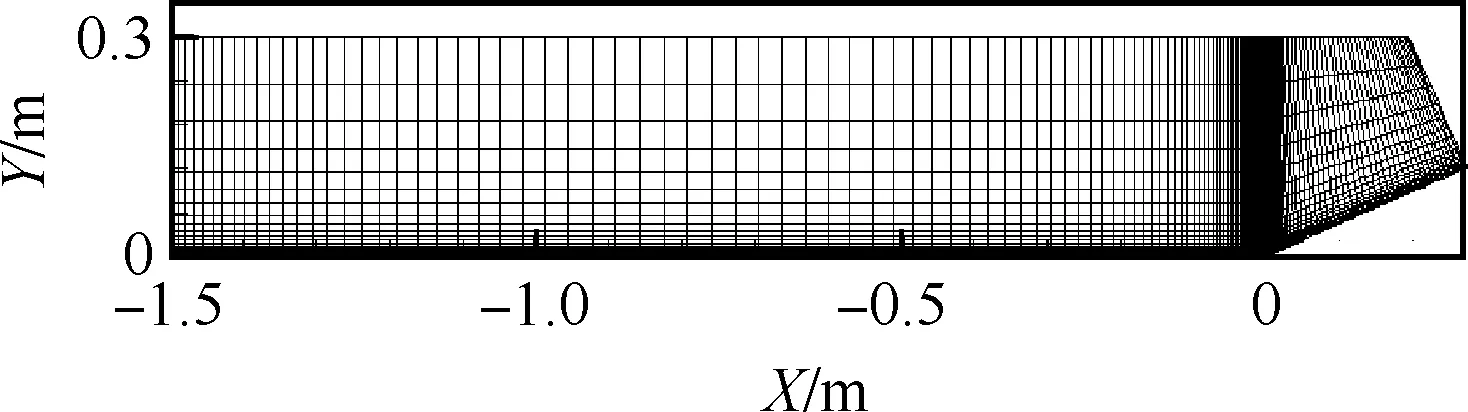
图4 压缩拐角网格示意图Fig.4 Compression corner mesh

图5给出了壁面距离=0.001 mm和1 mm网格计算消耗的计算时间和平均残差RES之间的对比,从图中可知粗网格=1 mm在下降到残差10时,消耗的计算时间仅为密网格=0.001 mm 计算时间的1/4。

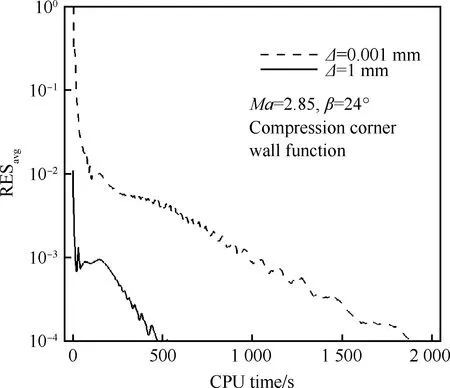
图5 压缩拐角24°收敛曲线Fig.5 Residual curves of 24° compression corner

图6给出了不同网格间距湍流边界层内速度分布,当不使用壁面函数时(如图6(a)所示),随着第1层壁面网格距离的增大,边界层内速度分布和实验值偏差逐步扩大,对于壁面网格间距=1 mm网格,和实验值差异最大可以达到30%。图6(b)给出了使用壁面函数后的速度分布,从图中可知网格从最密的=0.001 mm逐渐变稀到=1 mm边界层内速度分布依然和实验值高度吻合,表明壁面函数的应用明显提高了计算结果精度。

图6 湍流边界层速度分布Fig.6 Velocity distribution in turbulence boundary layer

图7给出了不同网格间距时压缩拐角壁面摩擦系数分布,从图中可知=0.001 mm密网格分离前湍流边界层摩擦系数同实验值吻合较好,且可以准确模拟分离区起始位置,分离区再附位置稍落后于实验值,再附区之后摩擦系数较实验值有明显偏差。文献[27]使用雷诺应力模型(Reynolds Stress Model, RSM)和Launder-Sharma-湍流模型对该算例进行了数值模拟,再附区之后均出现了高估摩擦系数的现象,其中RSM模型预测值为实验值的3倍左右。随着网格间距增大,壁面摩擦系数同实验值差异越大,其中粗网格=1 mm预测的摩擦系数在分离区前比实验值低80%,严重低估摩擦系数。图7(b)给出了使用壁面函数后压缩拐角壁面摩擦系数分布,其中粗网格的预测能力相较图7(a)得到大幅提升,分离区前后粗网格摩擦系数增加了10倍之多。

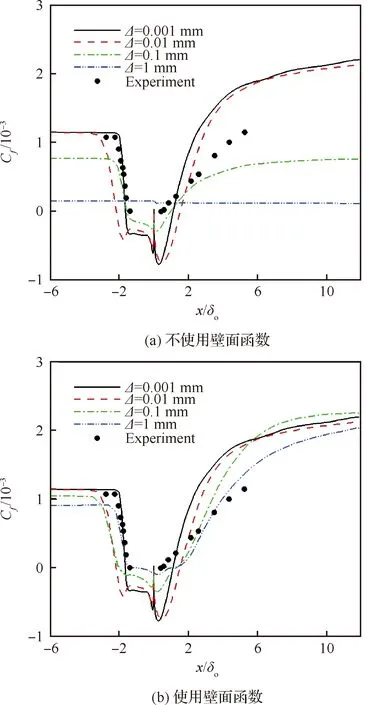
图7 压缩拐角摩擦系数分布Fig.7 Skin friction distribution for compression corner

3.2 高速飞行器

本算例用于检验标准壁面函数对于复杂的工程外形的气动力预测能力。飞行器外形类似于美国X-51吸气式高速飞行器,包含V尾、进气道、机翼、安定面等部件。飞行马赫数为4.0,雷诺数来流压力2 634 N/m,来流温度为69 K,绝热壁,攻角范围-8°～8°。为了保证数值预测精度,对进气道唇口附近网格进行了十分精细的网格设计,进气道内部采用O型网格。在飞行器表面生成若干层(包含41个点)较密的网格,安定面、尾舵、内流道等都采用了O型网格,在此基础上再向空间拓展,半场密网格约900万,第1层网格距离为2×10mm。稀网格将壁面O型网格修改为13个点,其他方向网格保持不变,第1层网格距离为0.1 mm,半场网格560万,进气道内密网格和稀网格的对比见图8,其中图中左边界为对称面、上边界、下边界和右边界为壁面条件。

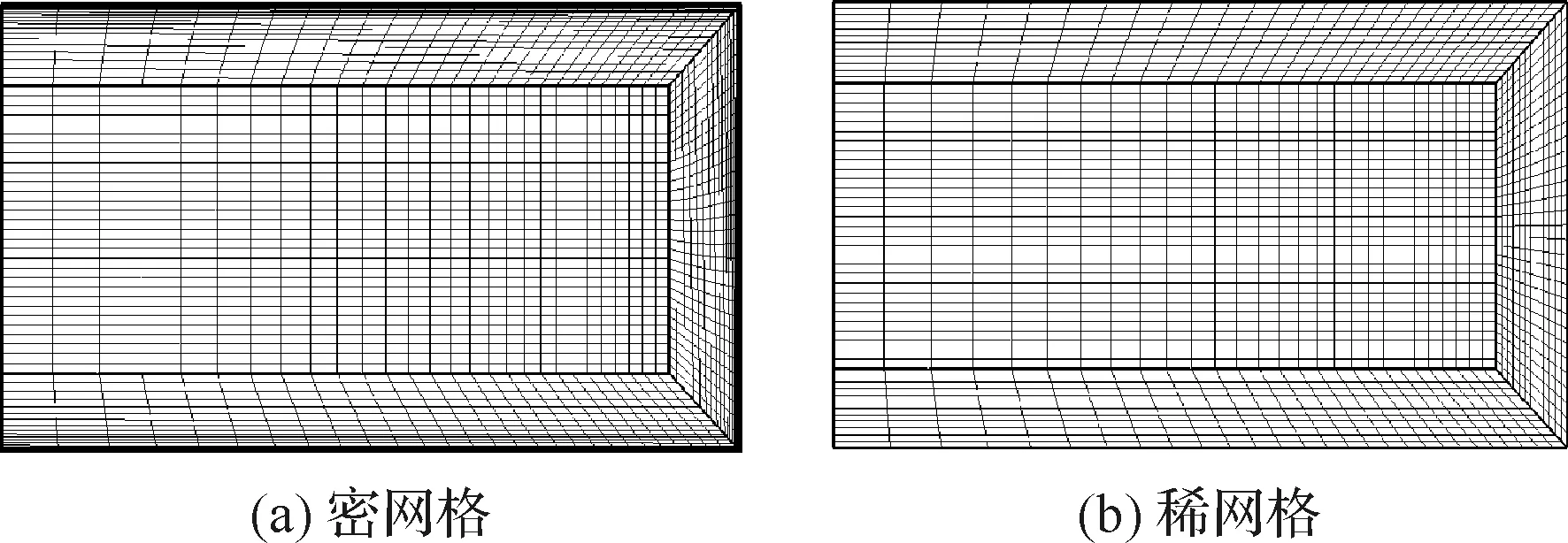
图8 进气道内网格对比Fig.8 Comparison of inlet meshes

图9给出了高速飞行器对称面马赫数云图和压力等值线,展示进气道内复杂的波系结构,且随着攻角的增加,进气道前缘产生的入射激波增强,入射激波和前体湍流边界层干扰增强,在壁面附近产生的分离涡逐渐增大。

图9 高速飞行器不同攻角马赫数云图和压力等值线Fig.9 Pressure iso-lines superimposed on Mach number contour for high-speed flight vehicle with different angles of attack

附面层网格变稀后,仅对局部流场产生影响,其中入口处分离区大小发生明显变化,图10选取攻角=8°给出了高速飞行器唇口附近压力云图和流线。图中:WF0表示不使用壁面函数;WF1表示使用壁面函数。从图中可知唇口产生的入射激波和上表面的边界层发生激波边界层干扰,在上表面形成一个小的分离区,其中图10(a)中给出的密网格结果可观察到明显的分离区,而稀网格不使用壁面函数时(见图10(b))模拟出的分离区小得多,图10(c)中稀网格使用壁面函数后得到的分离区大小和密网格更为接近,使得整个进气道入口处的波系结构也更靠近密网格结果。

图10 高速飞行器唇口附近压力云图和流线Fig.10 Stream lines superimposed on pressure coefficient contour for high-speed flight vehicle near inlet

图11给出了进气道内上表面壁面压力系数对比。由于进气道内存在复杂的波系结构,在进气道上表面压力系数呈现出多个波峰和波谷,稀网格不使用壁面函数时和密网格之间差距较大,表明稀网格不能准确捕捉进气道内激波位置,而稀网格使用壁面函数后整体预测精度提高,其和密网格之间的偏差减小。图中在进气道入口处对压力系数进行了放大,即图10中相应位置,其中由于稀网格不使用壁面函数时不能预测壁面附近激波边界层干扰产生的分离区,而使用壁面函数后不仅精确预测分离区位置,且可得到和密网格相似的压力系数曲线,高压区预测偏差从15%减少到2%。

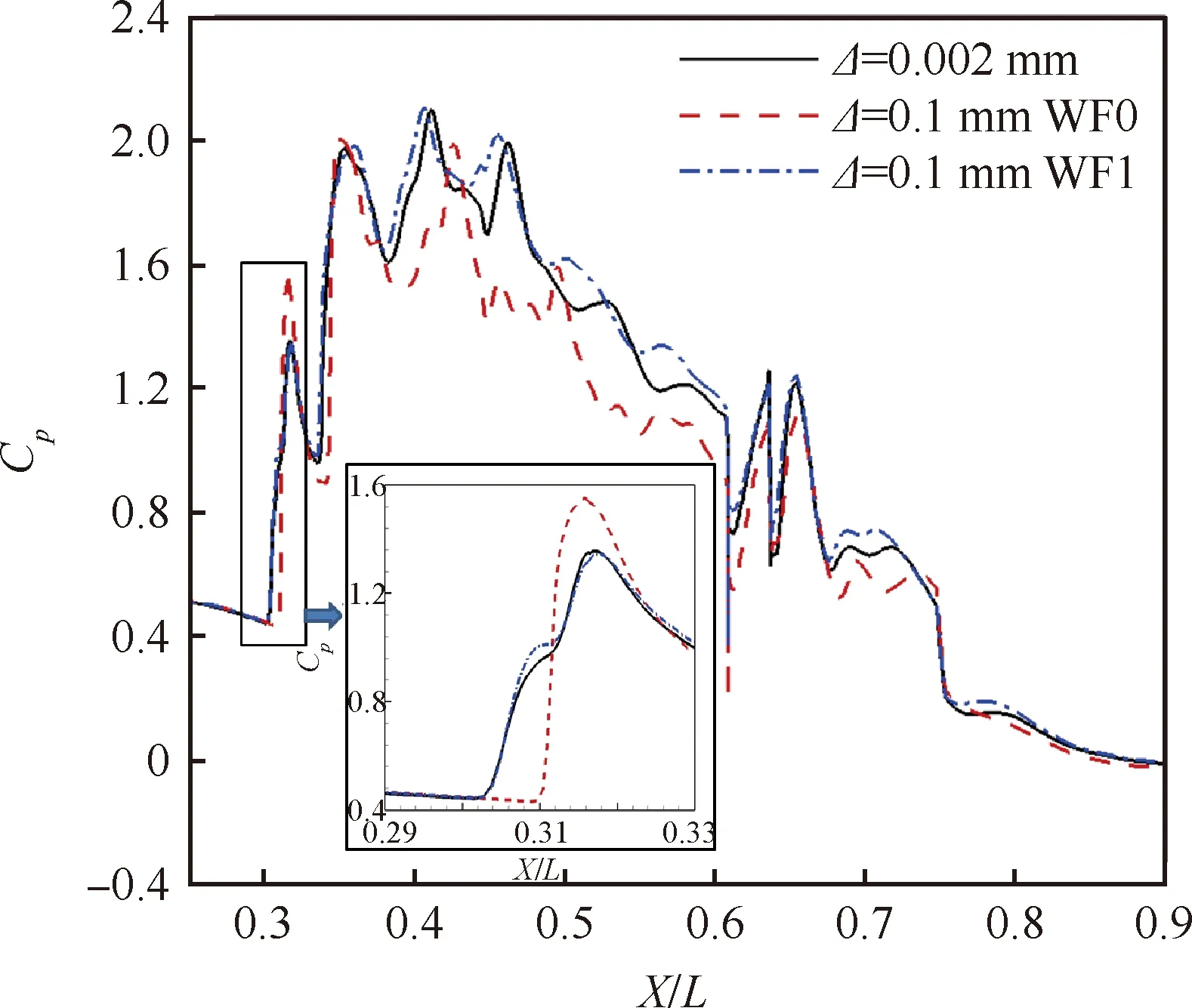
图11 进气道内压力系数曲线对比Fig.11 Pressure coefficient comparison in inlet

图12给出了相同计算设置的情况下(仅附面层网格和壁面函数使用情况不同),计算相同的步数消耗的计算机CPU时间对比,从图中可知减少附面层网格后计算时间减少了40%左右,而开启壁面函数后计算量相对仅增加了1%。

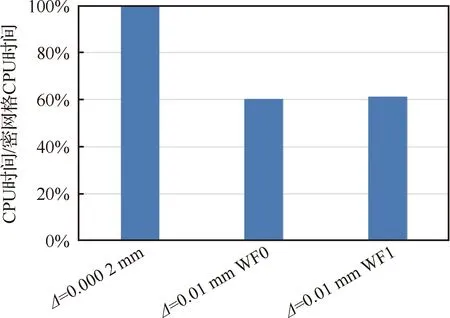
图12 相同计算设置消耗CPU时间Fig.12 CPU time consumption with the same numerical setup

图13给出了轴向力随CPU时间的收敛曲线,从图中可知密网格整体轴向力的收敛较慢,轴向力系数处于缓慢下降状态,稀网格整体收敛速度较快,整体看可大致节约60%的计算时间。

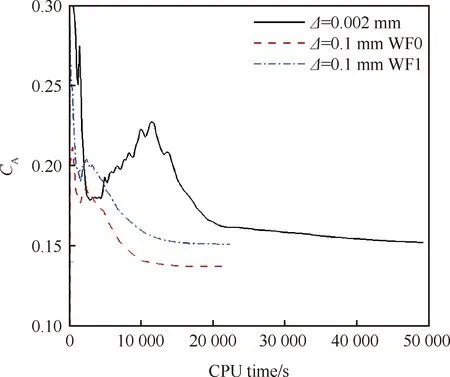
图13 轴向力收敛曲线Fig.13 Convergence curves of axial force

图14给出了轴向力系数随攻角变化,随着攻角增加轴向力系数增加,其中图14(a)给出了轴向力系数摩擦力分量A-,摩擦力占整体比例为37%～50%,当粗网格不采用壁面函数时,严重低估摩擦力,和密网格结果相差40%左右,而使用壁面函数后,和密网格差异在4%之内。图14(b)给出了轴向力系数压力分量A-,从图中可知不使用壁面函数时和密网格相差10%左右,使用壁面函数后相差3%,计算精度的提高主要得益于使用壁面函数后对分离区的模拟精度提高,如图10 所示。整体轴向力如图14(c)所示,整体轴向力粗网格不使用壁面函数时和密网格差异在11%左右,而使用壁面函数后差异缩小到2%以内,有效提高了轴向力预测精度。

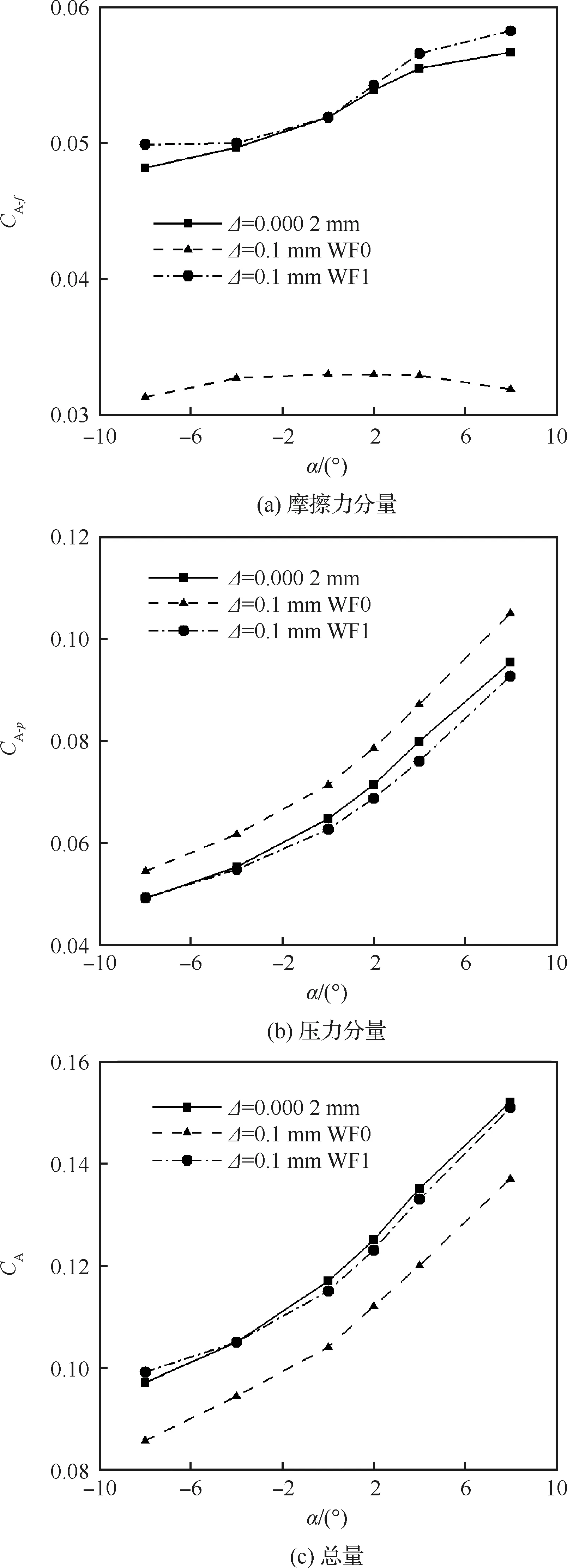
图14 高速飞行器轴向力随攻角变化曲线Fig.14 Axial force variation with different angles of attack for high-speed flight vehicle

4 结 论

基于国家数值风洞可压缩流动气动力数值模拟平台,开展适用的壁面函数方法研究,结合工程常用的SST-两方程模型,通过子迭代的形式计算摩擦速度,在达到预定收敛准则后通过更新虚拟点湍流黏性系数来实现湍流模型与壁面函数的耦合,并通过典型二维算例进行验证和工程复杂外形进行考核验证,通过比较不同网格间距时壁面函数开关对数值结果的影响,得到结论如下：

1) 壁面函数可有效提高壁面速度型预测精度,从而提高壁面摩擦系数的预测精度,对于简单外形摩擦系数大约可提高80%,对于工程复杂外形摩阻预测精度可提高36%。

2) 壁面函数可显著放宽第1层壁面距离,减少网格总量,节约计算时间。对于简单外形无量纲壁面距离≤200范围内,均可准确模拟湍流边界层速度分布。

3) 对于工程外形内外流一体化数值模拟,壁面函数在减少壁面网格距离和数量的同事,可准确模拟进气道内复杂的激波边界层干扰,激波反射等现象。

总的来说,通过壁面函数可获得和密网格相近的预测结果同时,有效降低湍流模拟对第1层网格高度的限制,大幅节约计算时间和计算内存,但壁面函数在工程外形上的应用准则,还需进一步研究。由于随着马赫数的增加,Navier-Stokes方程中的动量方程和能量方程耦合作用加强,而本文的壁面函数可视为动量方程在壁面附近的近似解,未考虑能量方程的影响,因此在高马赫数湍流模拟中,其预测精度很难得到保证,建议本文设计的壁面函数在来流马赫数≤5.0范围内的湍流模拟中使用。下一步将在国家数值风洞气动力计算平台中添加温度壁面函数,提高粗网格气动热参数的预测精度,进一步扩展壁面函数的适用范围。