基于提升卷积神经网络的航空发动机高速轴承智能故障诊断

韩淞宇,邵海东,*,姜洪开,张笑阳

1. 湖南大学 机械与运载工程学院,长沙 410082 2. 西北工业大学 民航学院,西安 710072 3. 中国航空工业集团公司西安航空计算技术研究所 民机事业部,西安 710065

航空发动机是飞机的“心脏”,其服役性能直接影响飞机的安全运行,每一次返厂维修的费用高达数百万美元。现代航空发动机正朝着高速重载,轻量化、高可靠性方向发展,使得发动机的工作条件愈发恶劣。作为航空发动机转子系统的“关节”,轴承长期于转速高且波动剧烈,负载大且变化明显的工况,将不可避免地产生性能衰退甚至引发各类故障。自动准确的航空发动机高速轴承故障诊断方法有助于提升航空发动机转子系统的运行安全性和维修经济性。基于振动信号特征提取构建浅层学习模型在航空发动机故障诊断领域已得到了广泛研究。然而由于航空轴承的动力学特性复杂、故障形式多样、原始振动信号具有强烈的非平稳性且含有大量干扰,致使浅层学习模型的诊断性能过度依赖信号预处理和人工特征提取。

人工智能的发展为故障诊断提供了新的思路和机遇,深度学习模型能在很大程度上摆脱对研究人员的诊断知识和工程经验的依赖,形成了端到端的诊断系统。近年来,在轴承等关键机械部件的故障诊断中受到了极大关注：姜洪开等对飞行器关键部件的深度学习智能故障诊断研究进行了系统性综述。Ding等结合了稀疏分解与卷积变分自编码器,实现了航空发动机主轴承的微弱故障特征提取。邵海东等提出基于提升深度迁移自动编码器的智能诊断方法实现不同机械设备间的迁移诊断。李巍华等改进了堆叠降噪自编码器,提高了轴承的故障识别准确率。杨世锡等提出了基于长短期记忆网络(Long Short-Term Memory, LSTM)和循环神经网络(Recurrent Neural Network, RNN)的智能故障诊断方法,能快速准确地区分滚动轴承故障类型。Zhang等将原始振动信号转化为二维图像,采用轴承数据集验证了该方法的有效性。此外,陈仁祥等提出了基于深度置信网络迁移学习的诊断方法；胡茑庆等提出基于经验模态分解的CNN(Convolutional Neural Network)故障诊断方法；汤宝平等构建多共振分量融合卷积神经网络；魏晓良等构建了基于LSTM和CNN的损伤程度识别方法；均对机电液系统的关键部件故障完成了准确诊断。

CNN减少了对故障诊断先验知识的依赖性,然而传统CNN的卷积核只有一个尺度,导致其难以提取具有较强鲁棒性的多尺度特征适应不同类型故障,也难以自适应不同的故障数据集。相较于传统CNN,多尺度CNN具有更丰富的视野域和泛化能力,能够同时对信号的全局性信息和局部特征进行提取,近年来成为研究的热点：张明德等阐述了多尺度卷积策略,利用轴承数据进行了验证。彭鹏等利用多尺度卷积网络实现噪声干扰下旋转矢量减速器的故障诊断。沈长青等提出了基于多尺度卷积类内自适应的深度迁移学习模型,有效诊断了变工况下轴承的多种故障模式。

多尺度CNN为故障诊断提供了新的思路,然而,现有研究多是基于平衡数据样本开展。实测的航空高速轴承故障样本远小于健康样本,在健康样本与故障样本不平衡时,深度学习模型诊断结果容易向大样本偏斜,导致诊断性能的下降。数据增强和重采样方法对小样本进行数量补偿是解决数据不平衡故障诊断问题时常采用的策略,如利用生成对抗网络(Generative Adversarial Network, GAN和合成少数类过采样技术(Synthetic Minority Oversampling Technique, SMOTE产生与原始数据样本近似的生成数据样本,平衡故障数据和健康数据之间的数量差异。然而,通过GAN进行训练对样本数量要求严苛,训练样本太少难以保证训练效果,训练样本太多会脱离发动机的实际工况；利用SMOTE扩充样本存在盲目性,可能导致样本混叠,增加故障诊断的难度。此外,生成样本会增加大量时间成本,因此更高效的研究工作需要展开,提升不平衡数据下端对端的轴承故障诊断性能。

为自动准确地诊断不平衡数据下航空发动机高速轴承的各类故障,提出了一种提升卷积神经网络：多尺度卷积网络用于提取数据的多尺度特征,使提取特征更具代表性；自适应权重单元用于提升相关特征的重要性,减少非相关特征的影响；LSTM进一步处理加权融合特征,增加特征的鲁棒性；采用Focal Loss损失函数,提升网络模型对故障样本的关注程度。航空发动机高速轴承模拟试验台的振动加速度数据集证明了所提方法在样本不平衡下故障诊断的有效性。

1 CNN和LSTM基本理论

1.1 CNN

由于权值共享,鲁棒性好等优点,CNN在故障诊断中得到了广泛应用。常见的CNN主要由卷积层,池化层,批量归一化层和激活函数构成。卷积层的主要作用在于提取输入信号的相关特征；池化层对卷积层提取的特征向量进行降维处理,进一步减少优化参数的数量,降低训练过程中过拟合的可能；常见的池化方法包括最大值池化和平均值池化；批量归一化层通过规范化手段将神经网络的任意神经元输入修正至标准正态分布,使训练时每一批次的分布相似,避免了梯度离散的问题,提高了神经网络的表现性能；激活函数的选择对网络模型的诊断准确率有显著的影响,常见的Sigmoid函数随着训练次数的迭代容易导致梯度消失,ReLU函数有效地解决了这一问题,但随着神经网络层数的加深会导致神经元死亡,Swish函数综合了两者的优点,在避免梯度消失的同时提高了迭代速度,不同数据集的验证证实其分类准确率高于ReLU函数,鉴于此,采取Swish作为所提模型的激活函数。

采用一维CNN直接处理振动信号更为合适,其运算可定义为

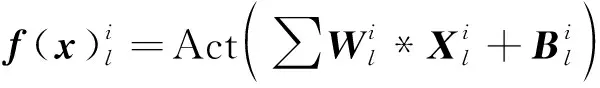
(1)

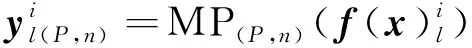
(2)

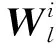
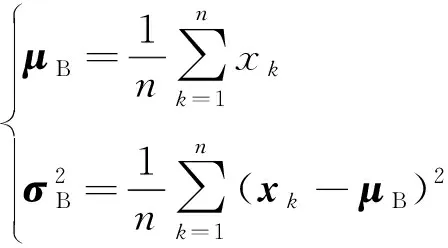
(3)

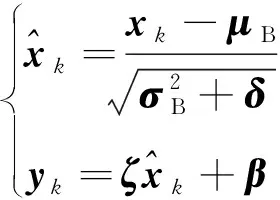
(4)

1.2 LSTM

CNN对时序信号的前后联系不敏感,RNN被证明能够更好学习时间序列中隐藏的发展趋势。作为RNN的变体,LSTM解决了RNN记忆容量有限,易产生梯度离散的问题,对长时间序列有更强的适应能力。结合CNN和LSTM,能从空间和时间两个维度实现对样本表征性信息更全面的提取。

LSTM通过引入遗忘门,输入门,输出门等门结构,状态向量,内存向量对循环神经网络进行了改进,提高了网络的表现性能。遗忘门作用于内存向量,控制之前的系统状态信息对系统当前时刻状态的影响,并对记忆内容进行筛选；输入门通过更新实时状态向量来控制系统对输入的接受程度,并通过tanh函数将输入数据进行压缩；输出门计算系统的输出,并根据输出完成对当前状态向量的更新：

=(*[-1,]+)

(5)

′=tanh(*[-1,]+)

(6)

=(*[-1,]+)

(7)

=×′+×-1

(8)

=(*[-1,]+)

(9)

=×tanh()

(10)

式中：(·)为sigmoid激活函数；为上一时刻的状态向量-1和当前时刻输入与遗忘门之间的权重矩阵；为相关偏置；为遗忘门的输出；、分别为、-1同输入门之间的权重矩阵；、为相关偏置；为输入门的输出；′为候选单元状态,和系统前一时刻内存向量-1共同决定系统当前时刻的内存向量;为-1、同输出门之间的权重矩阵；为相关偏置；为输出门的输出；为更新之后当前时刻的状态向量。

2 所提方法

2.1 多尺度特征提取网络

准确故障诊断的关键之一在于提取特征是否能够反映不同类型信号的差异性,单尺度的卷积核只能对信号的特定周期进行覆盖,提取特征时缺乏自适应性,难以在不同的机械设备故障诊断中得到应用。多尺度特征提取网络将不同尺寸的卷积核作用于不同的卷积单元,其不同卷积层视野域的迭代计算公式为

=(+1-1)+

(11)

式中：为卷积核的尺寸；为卷积步长；为视野域；下标为卷积层数。

当步长和迭代次数一定时,卷积核的大小反映了视野域的大小。小尺寸的卷积核更关注数据局部之间的联系,注重定位信号中的关键信息,大尺寸的卷积核利于提取信号的全局特征。将不同大小卷积核的卷积网络并行作用于同一信号,能学习到信号不同尺度的抽象特征,从多个尺度挖掘具有识别性的振动信息,增强网络故障特征识别的鲁棒性。组合不同尺寸的卷积核能够适应输入信号的改变,使模型具有更强的泛化能力。

多尺度特征提取网络采用不同大小的卷积核对输入信号的视野域进行感受,不仅能够降低选择卷积核尺寸的经验要求,更能提取鲁棒性好的多尺度特征。相比于单尺度特征,多尺度特征更能体现对不同故障数据的描述。所提方法的多尺度网络构建了相同形状的平行通道,采用不同大小的卷积核搭配不同数量的过滤器提取样本的多尺度特征。为了丰富特征的视野尺度,卷积核尺寸应该覆盖一定的范围,选择单数的卷积核,能够匹配数据的中心点,不易产生特征偏移,因此不同平行通道的卷积核尺寸设置为：3、11、17。此外,每个平行通道添加了旁路连接,利用大小为1的卷积核对信号的关键信息进行定位。

多尺度特征提取网络的有关结构参数和示意图由表1和图1给出,过程可以描述为

(12)

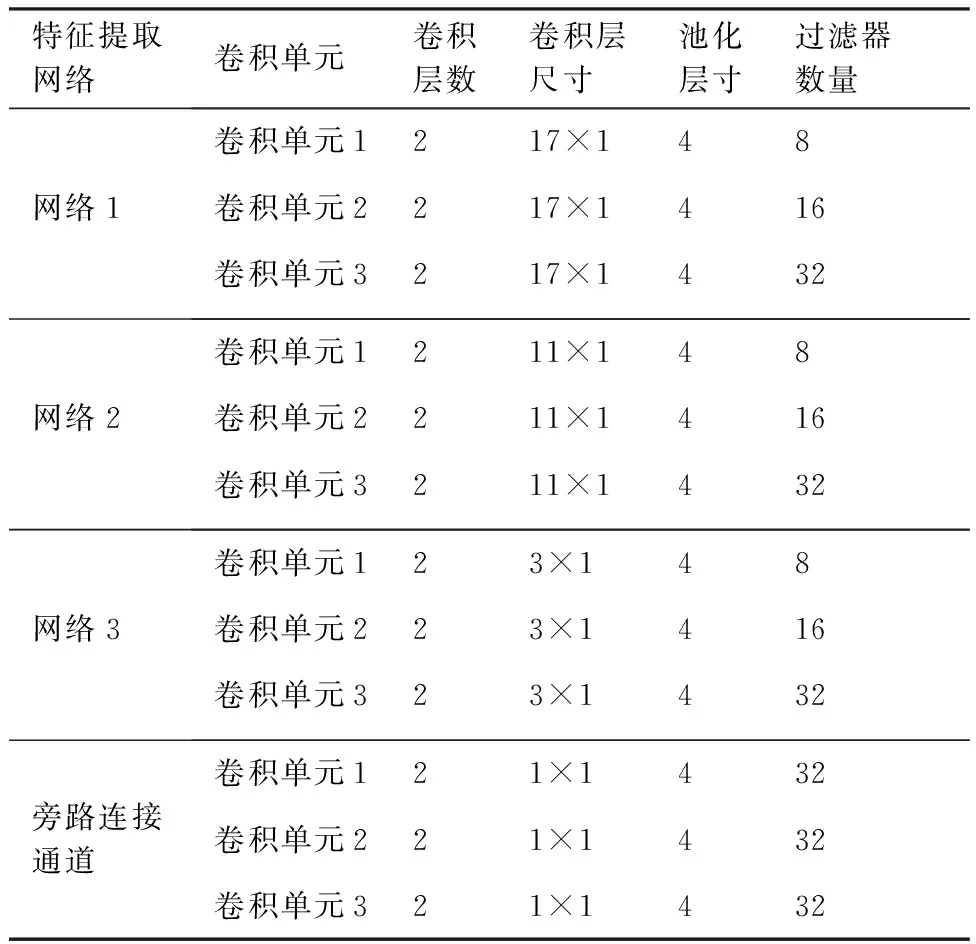
表1 多尺度特征提取网络结构参数

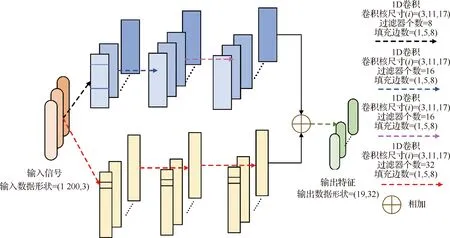
图1 多尺度特征提取网络结构示意图Fig.1 Structure of multiscale feature extraction network

2.2 自适应权重单元

通过多尺度特征提取网络提取的特征具有同等的重要性,然而不同的特征对故障诊断结果理应有不一样的贡献率。为了提升相关特征的贡献,降低非相关特征对故障诊断结果的干扰,设计了自适应权重单元对多尺度特征进一步处理。如图2所示,首先利用卷积层和最大池化层对输入特征进行压缩,使特征的重要性更容易被学习,然后利用大小为1的卷积神经网络为每个特征生成对应权重值,上采样层用于将权重还原至和输入特征相同的尺寸和维度,使特征权重值的形状和特征形状对应,便于乘积运算,最后通过Softmax函数将特征的重要性压缩至0～1之间。自适应权重单元本质上是所提方法中的网络连接层,利用分类损失函数进行训练,通过误差的反向传播即可完成有关参数的更新,从而每次训练过程中计算的特征重要性也会发生变化,即完成权重的自适应过程：

(13)

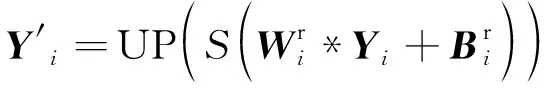
(14)

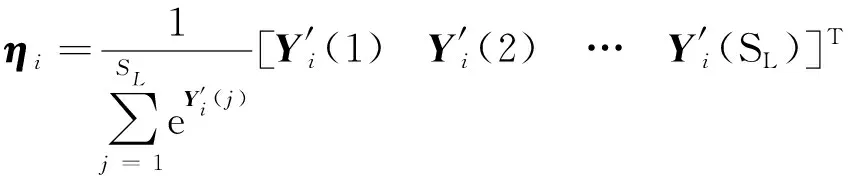
(15)

(16)

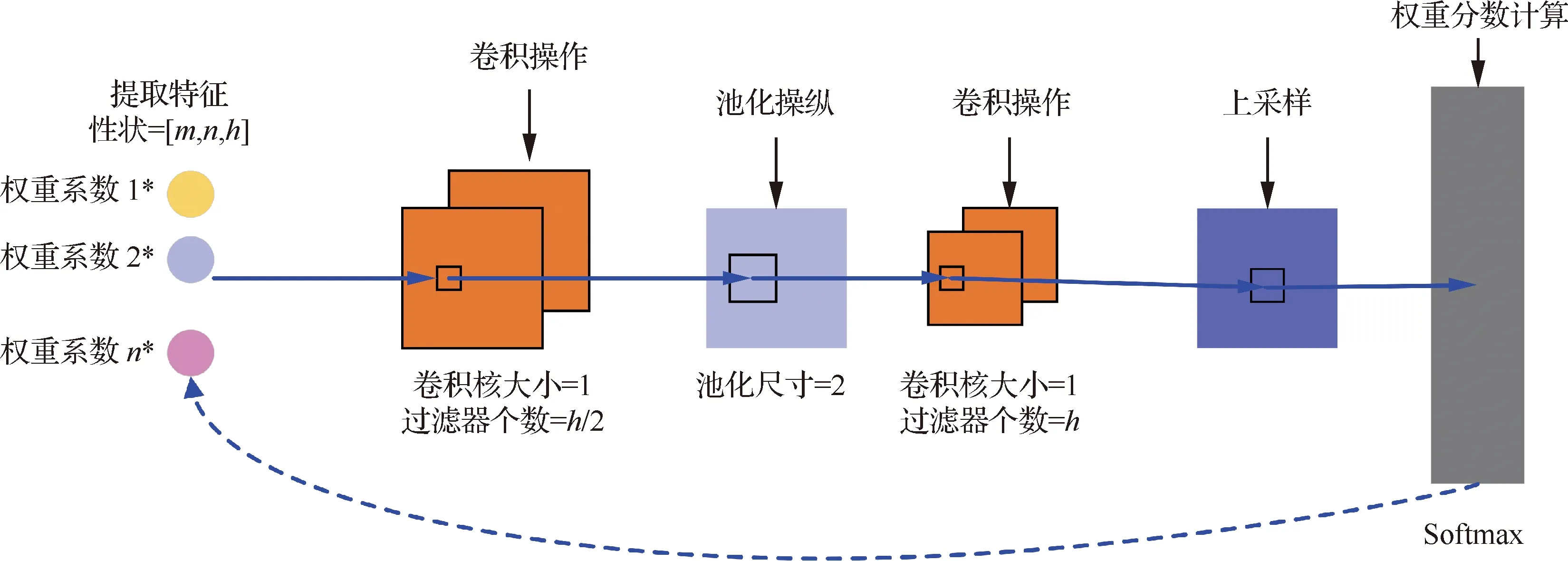
图2 自适应权重单元结构Fig.2 Structure of adaptive weight unit

2.3 Focal Loss

在样本高度不平衡时,损失函数同样对故障诊断性能产生了影响,传统的交叉熵损失(Cross Entropy Loss,CE Loss)通过计算真实分布与预测分布的差异计算损失值：

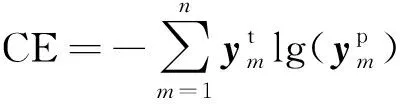
(17)

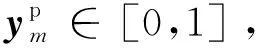
1) CE Loss将每一类型样本的分类成本视为相等,但训练过程中的总损失是所有样本的CE Loss之和。当健康样本远多于故障样本时,健康样本的损失值在总损失中占有足够高的比例,当对损失值进行最小优化时,由于故障样本的CE Loss对整体损失的贡献程度很小,当健康样本已经正确分类,整体的损失值就会降低到相对较低的水平,容易导致神经网络训练停滞。

2) CE Loss对易混淆样本的重视程度有待提高。如对于一个类的故障诊断问题,存在两个故障类别的样本,在某次训练过程中输出分别为[0.19…0.190.200.19…0.19],[0.10…0.100.500.10…0.10],在进行下一次训练过程时,前者被误判为其他样本的概率显然高于后者,提高易混淆样本的损失值所占比例有利于提高整体的故障诊断准确率。

针对上述问题,采用Focal Loss损失函数作为训练过程中的损失函数：

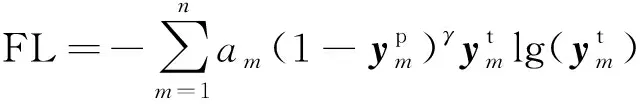
(18)

相较于CE Loss,做出如下改进：

1) 引入平衡因子平衡健康样本与故障样本之间的数量差异,其与不同故障类型的样本数量呈负相关关系。

2) 引入放缩因子用于降低易分类样本损失所占比例,增加易混淆样本的损失贡献,使训练过程中神经网络更关注易混淆样本。

2.3 所提方法步骤流程

所提方法用于不平衡数据下的航空发动机高速轴承故障诊断,主要步骤如下：

采用三轴振动传感器采集各种状态下航空发动机高速轴承振动加速度数据,其中健康样本远多于故障样本。

对振动加速度数据进行线性归一化处理,归一化的范围为[-1,1]。

将3个方向的振动数据简单拼接,使每个数据点包含3个方向的振动数据,并将数据集划分为训练样本和测试样本。

构建基于自适应权重和多尺度卷积的提升卷积神经网络模型,训练过程中采用Focal Loss损失函数。

测试样本进行故障诊断,不同的评价指标评估所提模型的诊断性能。

3 航空发动机高速轴承试验数据集描述

3.1 航空发动机高速轴承故障模拟试验台

采用的数据来自意大利都灵理工大学机械和航天工程系的航空发动机高速轴承故障模拟试验台,该试验台可测量航空轴承在不同高转速和不同重载荷下的振动加速度数据。

图3为实验平台,B1、B2、B3为3个轴承支座,A1和A2处各安装1个三轴振动加速度传感器,分别用于测量损坏轴承支架B1处和受外载荷最大B2处的振动数据。使用Rockwell工具在轴承内圈或滚子上产生不同大小的锥形压痕,模拟不同的故障类型,轴承不同健康状态的测量过程相同：首先在空载下以100 Hz转频(6 000 r/min)短暂运行,检查安装是否正确,正确安装后逐步改变外载荷的大小,并以100 Hz为步长提高。当轴的转速稳定后就通过传感器对振动数据进行测量,表2给出了转速和外载荷之间的试验组合。

图3 实验平台Fig.3 Experimental platform

表2 测试负载和旋转速度Table 2 Testing load and rotating speed

3.2 不平衡数据集构造

为模拟航空发动机轴承长期运行于高速和重载的真实工况,且进一步测试所提方法的故障状态识别性能,选取3种高转速(18 000、24 000、30 000 r/min)和2种大载荷下(1 000、1 400 N)的振动数据用于验证所提方法有效性,不仅可以更好地模拟航空发动机转速的波动,还可以提升故障诊断任务的复杂性。为了模拟训练样本的不平衡情形,将健康类别的训练样本设置为1 000个,故障类别的训练样本数量满足均值为50,方差为10的高斯正态分布,进行测试时,健康样本和各故障类型样本均设置为100个。传感器不同通道的数据体现了对故障类型的一致性描述,虽然在分布上有所差异,但本质上属于同构数据,采用直接拼接的处理方式不仅可以减少数量的损失,也能更全面探索不同通道间互补的信息。鉴于此,选择、、方向各1 200个数据点依次拼接成1 200×3的样本。共构建2个实验数据集T1和T2,相关的具体描述由表3和表4给出。

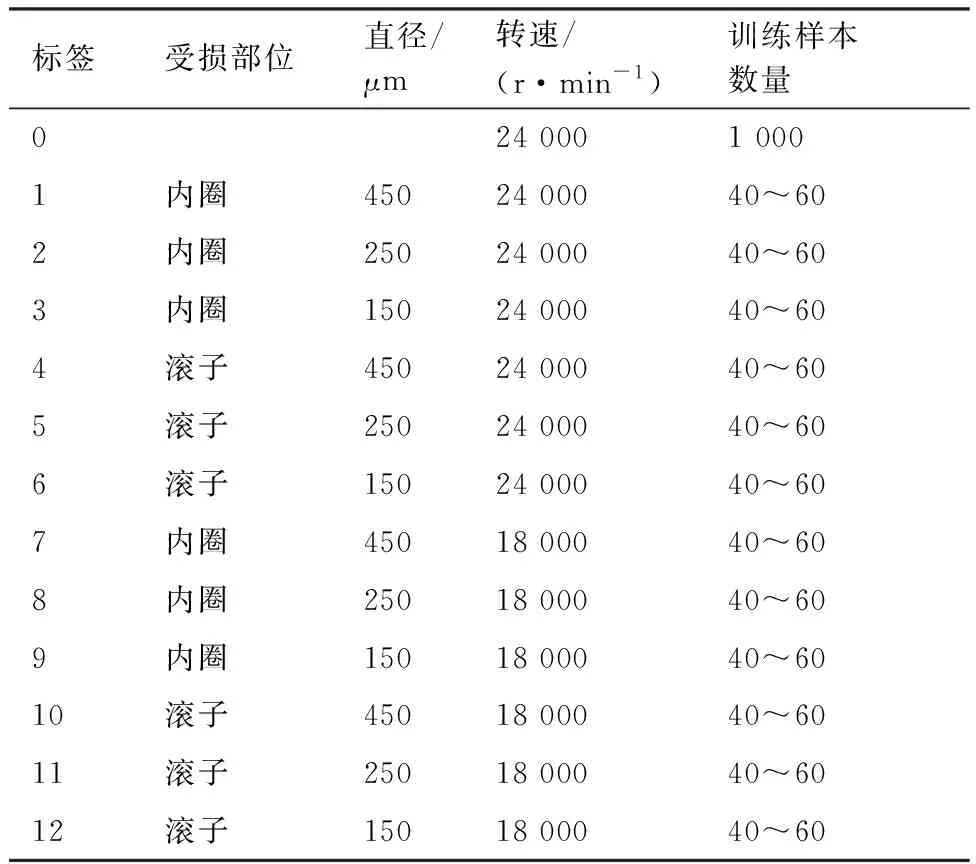
表3 数据集T1描述 (载荷=1 400 N)Table 3 Description of data set T1 (载荷=1 400 N)

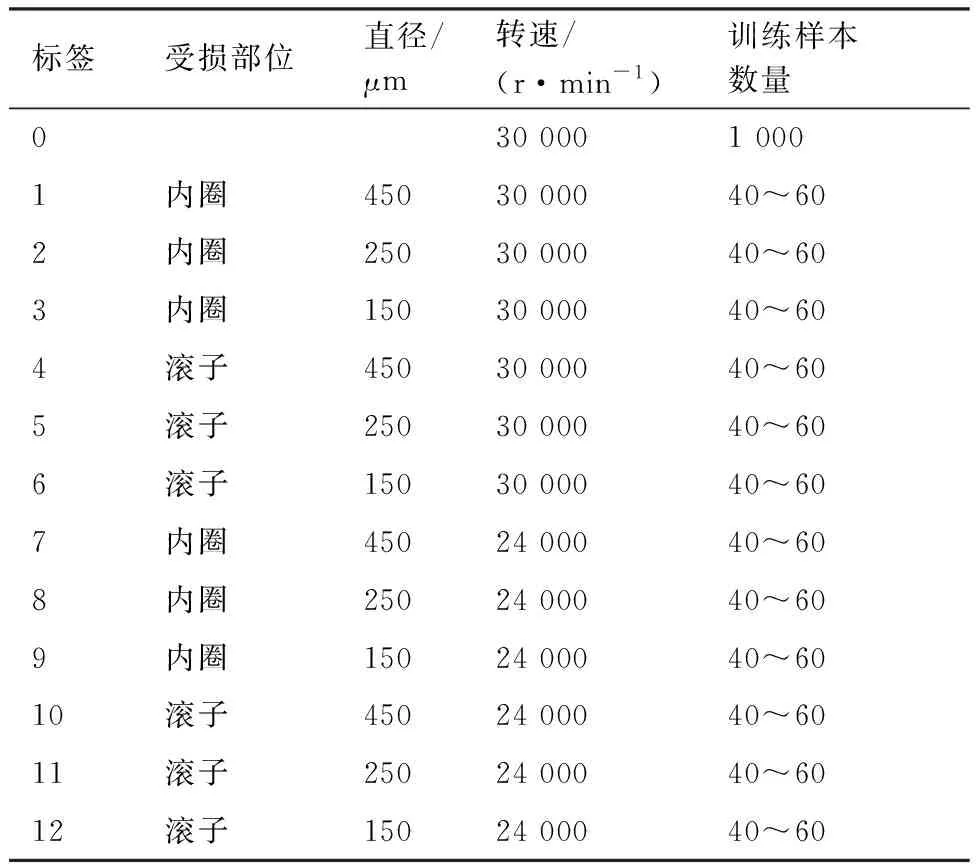
表4 数据集T2描述 (载荷=1 000 N)Table 4 Description of data set T2 (载荷=1 000 N)

4 案例验证

所提方法与目前常用的深度学习智能诊断方法对比,包括：CNN1 (CE Loss)、CNN2 (Focal Loss)、卷积自编码器和双向LSTM。CNN1和CNN2采用单一尺寸的卷积核,堆叠层数与所提方法相同,对比方法均采用ReLU函数作为激活函数。分别对数据集T1和数据集T2进行故障诊断。为防止随机误差对实验的干扰,所有的实验重复进行10次,并取实验的平均值作为该种方法的平均诊断准确率,具体的结果由表5给出。

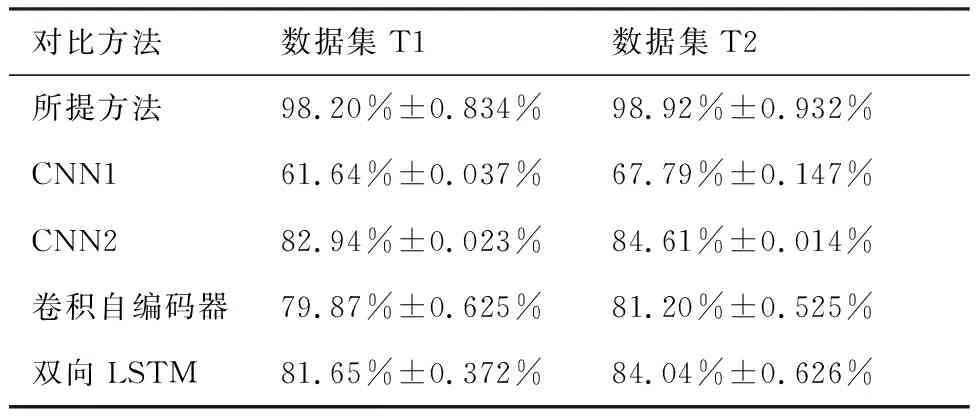
表5 不同方法故障诊断结果对比

案例运行环境简单介绍：CPU：i5-10400F；GPU：GTX1650；运行系统：Windows10；运行软件版本：Tensorflow2.1。案例中参数设置如下：设置为2；为第类样本数量占总样本数量的倒数再经过归一化处理后的值；迭代次数设置为100次；初始学习率为0.000 1,若训练过程中连续5次损失值未下降,学习率乘以0.85进行更新。训练过程中,CNN1采用CE Loss函数,其余所有方法均使用Focal Loss函数。

结果显示所提方法对数据集T1的平均诊断正确率为98.20%±0.834%,对数据集T2的平均诊断正确率为98.92%±0.532%,均高于其余对比方法。采用Focal Loss后,CNN2在诊断准确率上相较CNN1有了明显提升,分别提高了约20个百分点和17个百分点,但结果显示Focal Loss损失函数只能在训练过程中对小样本的数量进行补偿,并不能保证CNN能准确提取不同故障类型具有代表性的样本特征,因此CNN2相较CNN1,虽然故障诊断准确率有了提升,但由于提取的故障样本特征依然不具有充分的表征性,仍难以实现高性能的故障诊断。

当训练样本数量不平衡时,精确率和召回率是评估诊断性能的优良指标：

(19)

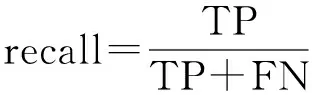
(20)

式中：pre为精确率；recall为召回率；TP为正样本预测为正样本的个数；FP 为负样本预测为正样本的个数；FN为正样本预测为负样本的个数。

图4和图5给出了训练过程中所提方法针对数据集T1、T2的故障诊断准确率,精确率,召回率的迭代变化曲线,进一步对所提方法的故障诊断性能进行评估。结果显示当训练次数超过20次之后,训练集的各项指标已经达到较高的水准,只在小范围内进行波动。当迭代次数达到100次时,各项指标都达到了100%的水准；测试曲线的各项指标略低于训练曲线,并未出现神经网络过拟合导致测试精度降低的现象,证明所提方法在训练样本不平衡的情况下针对测试样本的诊断性能也维持原有的高水平。

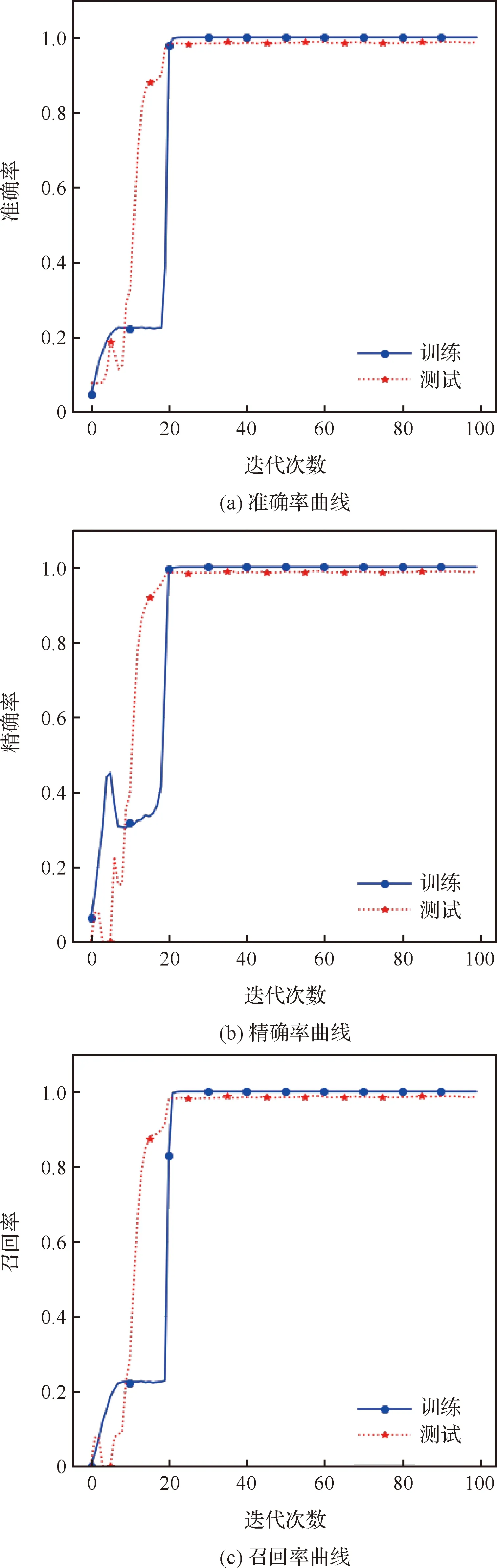
图4 评价指标曲线-T1Fig.4 Curves of evaluation indexes-T1

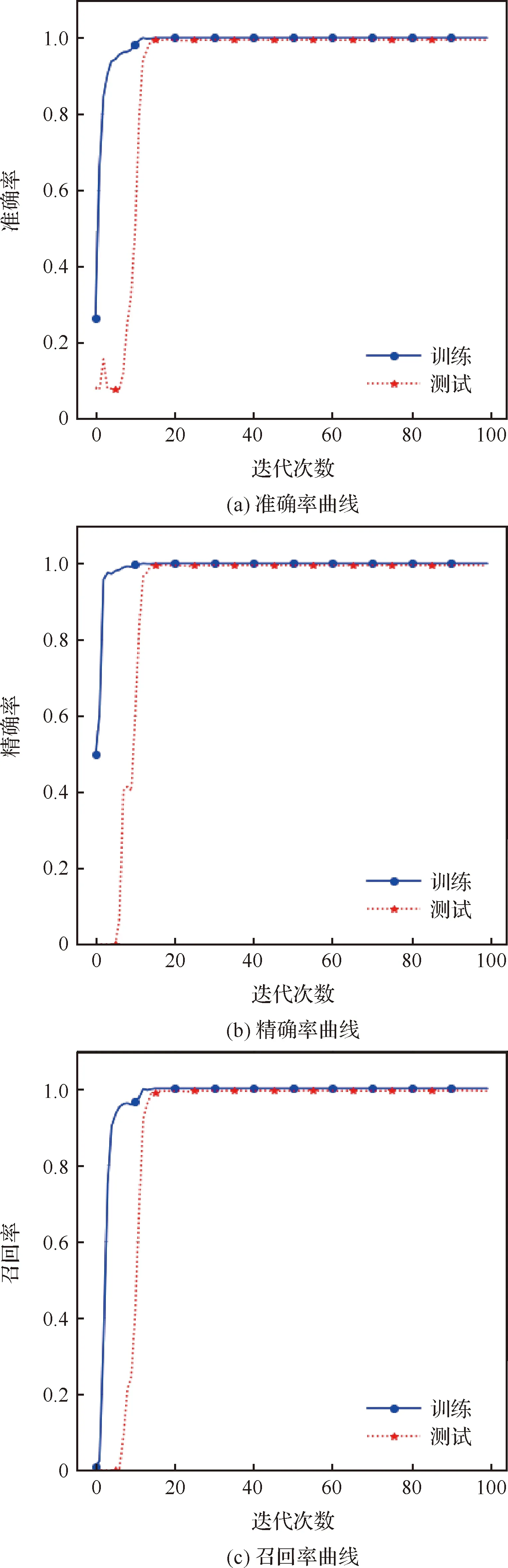
图5 评价指标曲线-T2Fig.5 Curves of evaluation indexes-T2

为更好评估模型的诊断性能,分别给出某次测试过程中所提方法关于数据集T1和T2的故障诊断混淆矩阵,如图6和图7所示。图中横坐标代表的是真实标签,纵坐标代表的是预测标签。

图6结果显示,在对数据集T1进行测量时,类别为1的样本诊断准确率为91%,被误分为类别3,8的比例分别为8%,1%；类别为2的样本诊断准确率为88%,被误分为类别4的比例为12%；类别为4的样本诊断准确率为91%,被误分为类别2的比例为9%,其余样本的诊断准确率均达到了100%。

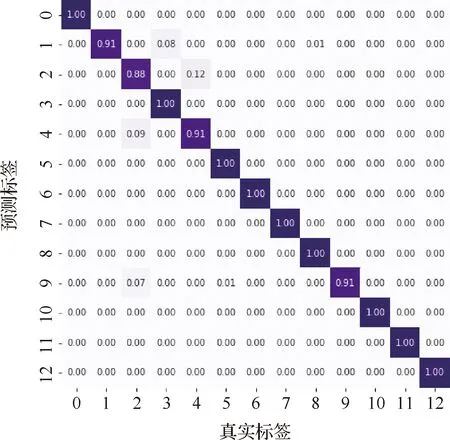
图6 所提方法诊断结果混淆矩阵-T1Fig.6 Confusion matrix of diagnosis results of proposed method-T1

图7结果显示,在对数据集T2进行测量时,类别为3的样本诊断准确率为71%,被误分为类别0的比例达到了29%；其余样本的诊断准确率均高于95%,其中类别1的诊断准确率为96%,少量样本被误判为类别0和类别3；除类别3,类别1外,其余样本的诊断准确率均达到了100%两实验集的混淆矩阵进一步证明所提方法在不平衡样本的情况下更能适应不同故障信号的变化,提取的特征具有较好的差异性,能够完成高准确率的航空发动机轴承故障诊断。

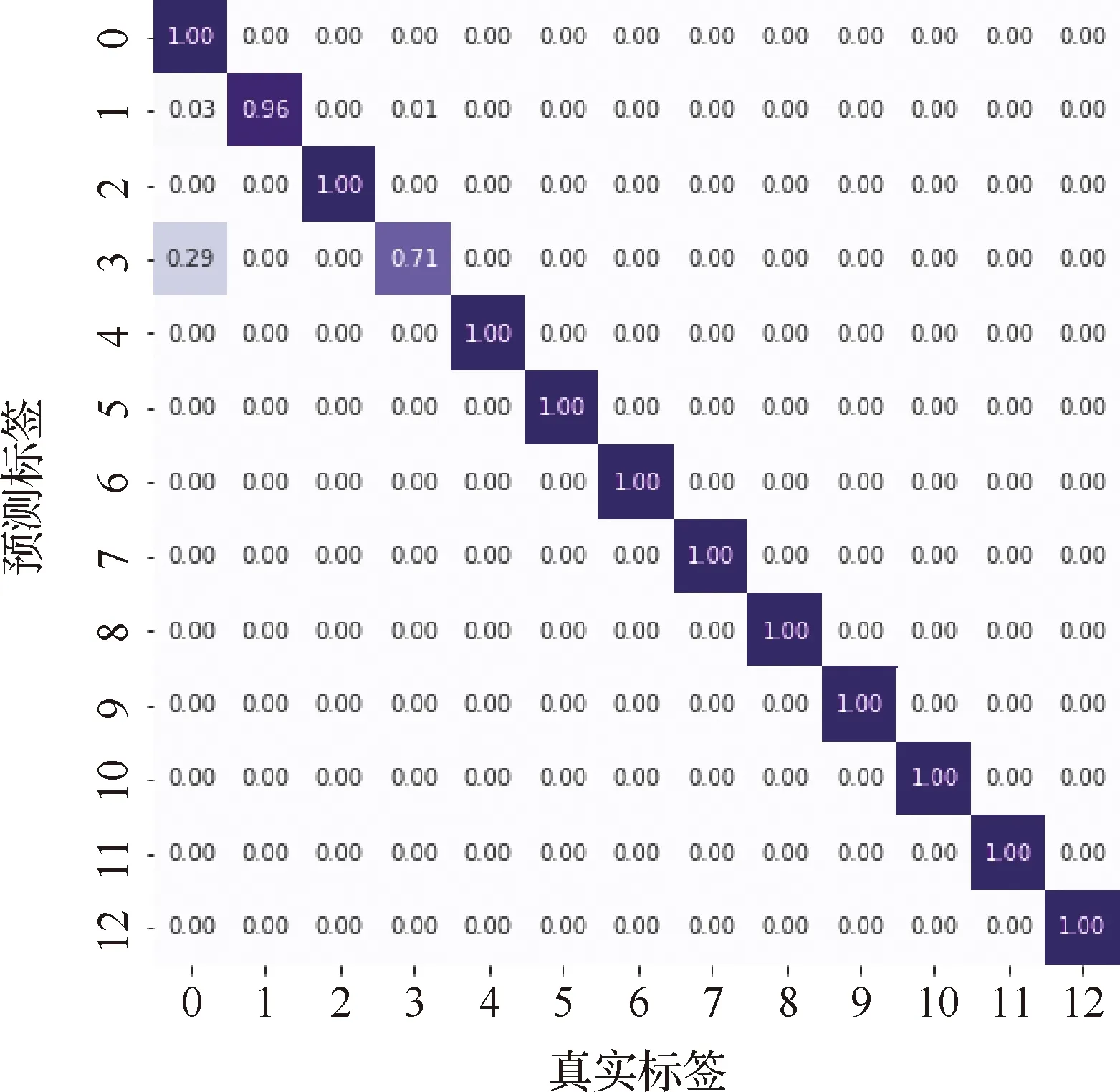
图7 所提方法诊断结果混淆矩阵-T2Fig.7 Confusion matrix of diagnosis results of proposed method-T2

采用T分布随机邻域嵌入(T-Stochastic Neighbor Embedding,T-SNE)方法可视化某次测试过程中CNN1,CNN2,和所提方法的最终输出特征,如图8和图9所示。

图8展示了3种对比方法对数据集T1进行故障诊断时提取特征的二维空间分布图。图像显示所提方法提取的特征在二维空间上的聚类非常清晰,相同类型样本之间的分布更加紧凑,只有少量不同类别样本的输出特征分布在临近的区域。结果同样显示CNN1和CNN2能够区分个别样本类型,提取特征在二维空间上形成聚类分布,但多数样本产生了重叠现象,证明单一尺寸卷积核可实现对某些类型振动信号特征的提取,但难以适应振动信号的改变,导致诊断准确率难以达到较高水平。

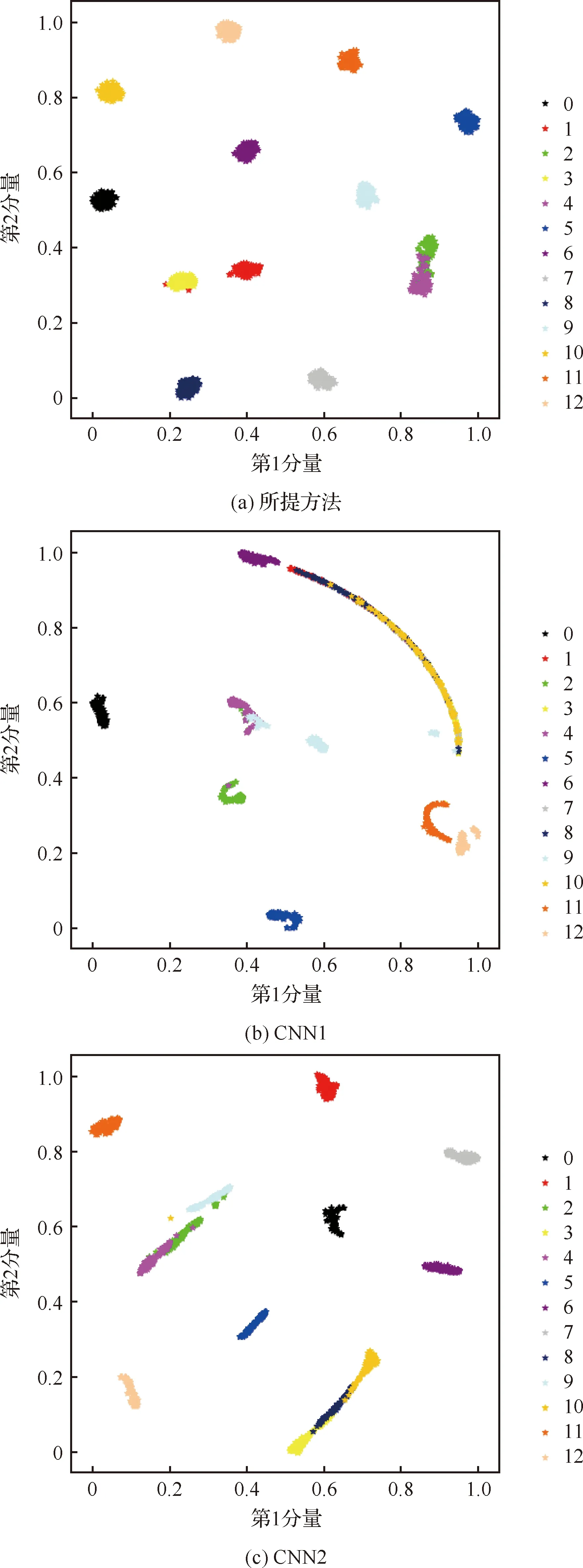
图8 特征二维可视化-T1Fig.8 Two-dimensional visualization of features-T1

图9展示了3种对比方法对数据集T2进行故障诊断时提取特征的二维空间分布图。相较于数据集T1、CNN1和CNN2能够识别更多类别的样本,Focal Loss提高了卷积神经网络对小样本损失的重视,使CNN2提取特征的聚类现象优于CNN1,但两种方法依然无法适应所有类型的输入信号,产生重叠的样本类别和数量依然多于所提方法。

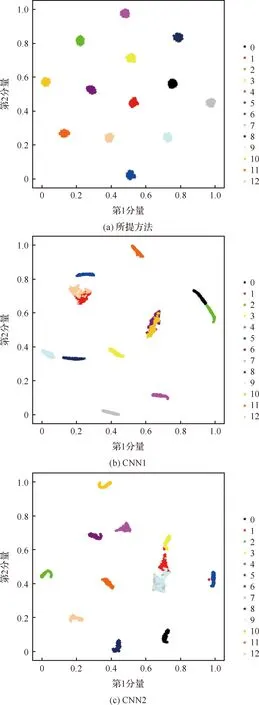
图9 特征二维可视化-T2Fig.9 Two-dimensional visualization of features-T2

两组数据集的特征二维空间分布图的对比证实了在不平衡数据集下,所提方法提取的多尺度特征具有更强的识别性,能够反映不同故障信号之间的差异。

自适应权重单元对特征重要性进行了区分,提高相关特征的重要性利于实现高性能的故障诊断。图10给出了训练过程中卷积核尺寸为17的特征提取网络提取特征的权重自适应过程,数据显示提取特征被赋予了不同的权重,其重要性得到有效区分。权重随着迭代进行而改变,当迭代50次和100次时,所提模型的分类准确率在峰值水平波动,对应的特征重要性也存在很大程度的相似,说明了自适应权重单元的必要性。

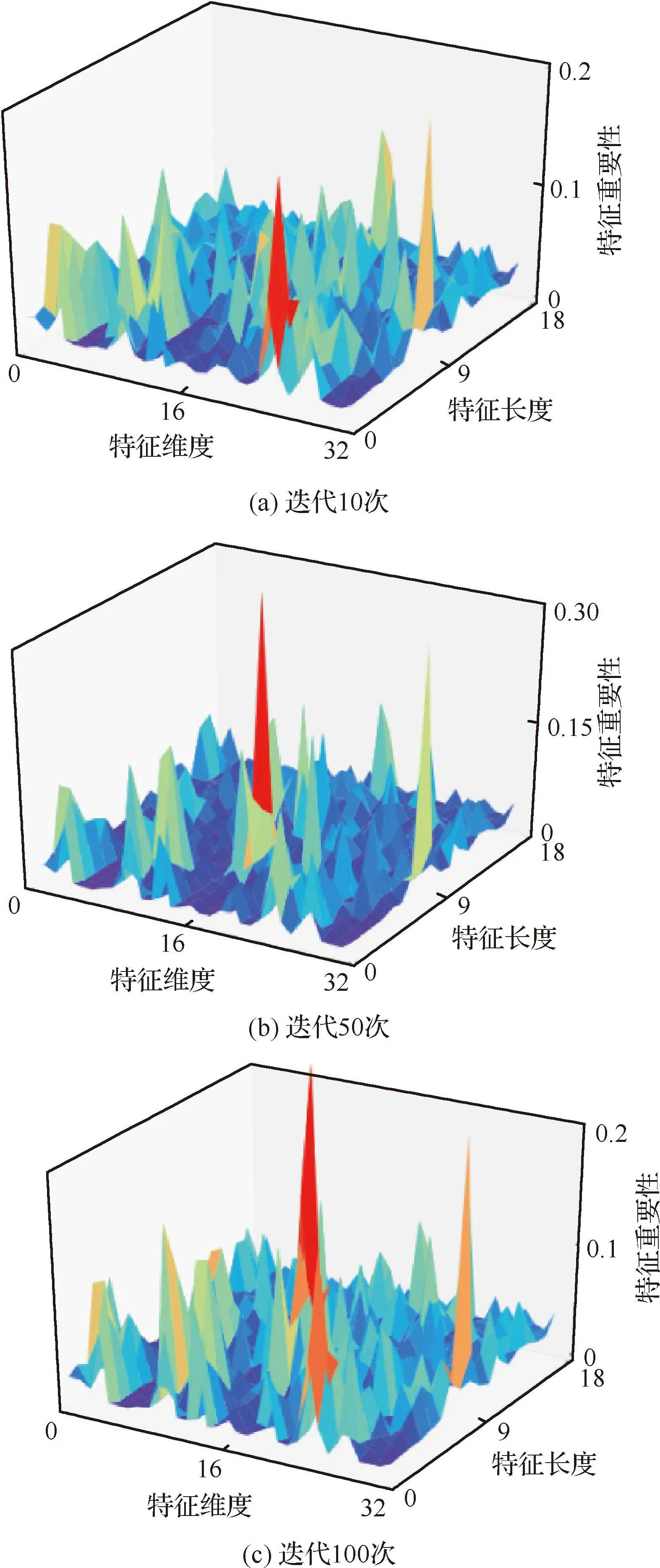
图10 特征权重自适应过程Fig.10 Adaptive process of feature weights

5 结 论

1) 相较于单尺度神经网络,多尺度卷积神经网络更能够适应不同的故障信号,具有更强的泛化能力,在样本不平衡时能够挖掘表征性特征,经过自适应权值单元的加权融合处理能使多尺度特征更具代表性,所提模型能够充分挖掘故障样本的信息,在样本不平衡条件下实现高性能的故障诊断。

2) 不平衡数据集下采用Focal Loss损失函数能够提高卷积神经网络对小样本和易混淆样本的关注程度,进而在一定程度上提高故障诊断的准确率。