吸气式电推进系统进气道结构对进气性能的影响

谢晓乐，李济源，王娴, 2,*，鲁海峰，韩先伟

1.西安交通大学 航天航空学院 陕西省先进飞行器服役环境与控制重点实验室，西安 710049 2.西安交通大学 机械结构强度与振动国家重点实验室，西安 710049 3.西安航天动力研究所 陕西省等离子体物理与应用技术重点实验室，西安 710100

超低轨道卫星飞行高度在120～300 km之间，与一般卫星相比，其优势在于更接近地球，因此在高精度地球监测、精确的重力或磁场测绘以及全球海洋气候探测得到广泛应用，受到世界各国密切关注。如欧洲航天局发射的地球重力场和海洋环流探测卫星，以及日本宇宙航空研究开发机构发射的超低轨道技术试验卫星。但同时也由于过低的飞行高度承受一定的大气阻力，需要借助推进系统补偿阻力，维持稳定工作。

目前卫星使用的化学推进系统和电推进系统都需要从地面上携带一定数量的推进剂，推进剂的数量直接限制了卫星的工作寿命。此外，携带过多的推进剂也增加卫星的发射质量，间接提高发射费用。为解决这一问题，研究人员提出了吸气式电推进系统。

吸气式电推进系统可以利用太空中稀薄气体作为推进剂，从而提高卫星的工作寿命，这个想法最早在1959年由Demetriades提出。使用轨道飞行器收集、液化和储存高空稀薄大气作为推进系统的推进剂。在这一设计方案的基础上，随后十几年，大量学者也相继提出了不同的推进方案，主要区别在于最终的能量来源不同，但都需要一个气体收集装置来收集气体。因此实现吸气式电推进，一个气体收集装置是必要的，并且由气体收集装置所供给推进剂的压力和数量应满足电推进器的实际工作需求，因此气体收集装置需要具备一个高的压缩比和收集效率。

目前，欧美日本等发达航天大国针对吸气式电推进系统的研究较为领先，如日本宇宙航空研究开发机构(Japan Aerospace Exploration Agency, JAXA)、欧洲航天局(European Space Agency, ESA)、BUSEK公司都先后提出了气体收集装置的相关设计方案。近几年，众多学者在此基础上，针对进气道的结构优化设计开展了大量研究。Romano等研究了进气道入口栅格通道长纵比对进气道进气性能的影响规律，发现栅格通道长纵比越低，进气道的压缩比和收集效率越高。Barral等推导了进气道的数学模型，分析了进气道长纵比对进气道进气性能的影响规律，并通过数值模拟验证了数学模型。Binder等分析了进气道入口栅格通道长纵比对进气道入口来流和内部回流通过率的影响规律。Erofeev研究了进气道长纵比与进气道末端粒子密度的关系。以上学者对进气道进气性能的研究都是采用被动收集气体的方案。Li等提出了一种主动收集气体的气体收集装置，通过实验分析了气体收集装置末端分子泵的性能，数值研究了气体收集装置入口端多孔板的进气性能。Romano等也从系统操作难度、系统功耗等方面分析了主动收集气体和被动收集气体的优劣。

关于吸气式电推进技术，欧美、日本等发达国家已经开展了大量研究，但公开资料少。兰州空间技术物理研究所和上海空间推进研究所对离子电推进和霍尔电推进开展了大量研究，研制出了离子和霍尔电推进系统，并在中国东方红系列卫星投入使用。除此之外，也有学者也进行了吸气式电推进系统气体收集装置的相关设计研究工作。

研究方法上，在地面实现高真空环境并获得高速稀薄来流气体开展实验研究十分困难；对于数值方法，高空大气极为稀薄，属于自由分子区域，已经不满足连续介质的纳维-斯托克斯(Navier-Stokes)方程，与之相对应的是玻尔兹曼(Boltzmann)方程，而直接求解Boltzmann方程相当困难。为此，Bird提出了直接模拟蒙特卡罗(Direct Simulation Monte Carlo, DSMC)法，该方法的正确性已在实践中得到证明，并且成为研究稀薄气体的一种强有力的工具。

综上所述，近几年国内外学者针对气体收集装置进气道结构的优化设计开展了大量工作。主要关注于进气道的长纵比，进气道入口是否有栅格结构及其长纵比对进气道气体收集性能的影响。有关进气道出口锥角和栅格的几何尺寸参数对进气道进气性能的影响规律的研究较少，且栅格对进气性能的内在影响机理未得到充分揭示。

本研究采用DSMC法，分析了进气道的长纵比、进气道出口锥角、栅格结构以及栅格结构的型式和尺寸参数对进气道进气性能的影响规律，并通过进气道内粒子运动轨迹揭示了栅格对进气道压缩比和收集效率的影响机理，为吸气式电推进系统进气道的结构设计和优化提供参考依据。

1 计算模型

吸气式电推进系统进气道二维数值模型如图1 所示。上下为固体壁面，左端进气道入口高度=0.6 m，入口来流特性参数参考表1，为来流粒子数密度，为来流速度，为来流温度，为进气道入口进入粒子数；为进气道出口粒子数密度，为进气道出口逸出粒子数；为进气道内粒子数，为进气道入口逸出粒子数。入口端设置栅格结构，为栅格板长度，和分别为栅格板厚度和层数；为右端进气道出口高度；为出口锥角；为进气道长度；进气道长纵比为=，入口高度与出口高度比值为=，压缩比为=，收集效率为=。

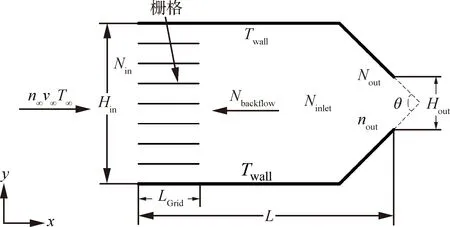
图1 进气道二维数值模型Fig.1 Two-dimensional numerical model of air-intake

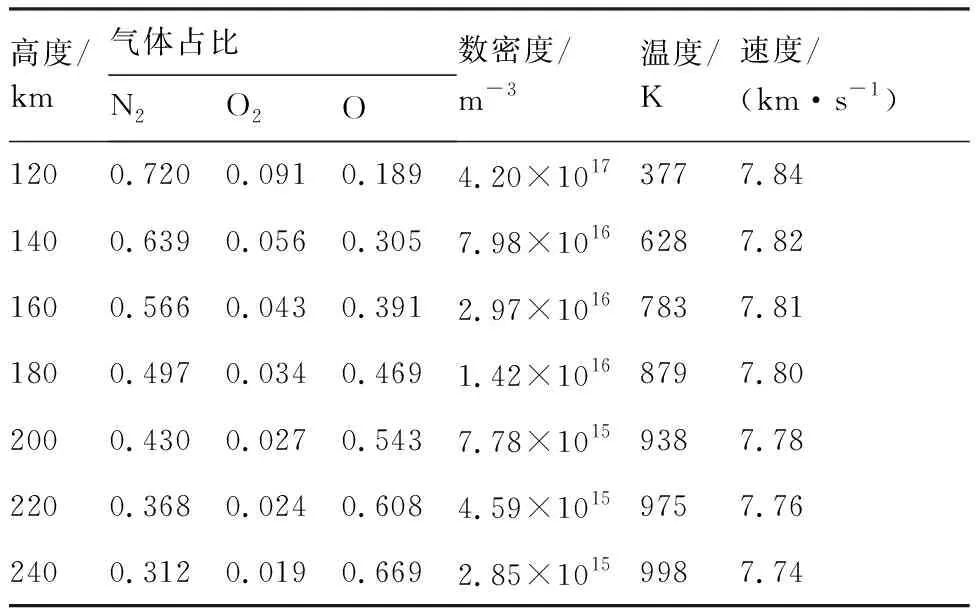
表1 大气特性参数[26]Table 1 Parameters of atmospheric characteristics[26]

2 数值方法

2.1 计算方法

研究采用直接模拟蒙特卡罗法开展，其基本思想是用有限个模拟粒子代替大量的真实气体粒子，在一定的时间间隔内将粒子的迁移运动与粒子间的碰撞解耦处理，通过直接跟踪模拟粒子的运动，记录各个模拟粒子的位置、速度和能量，最后以主网格为统计单元，将这些仿真粒子做统计平均，从而得到气体宏观状态参数。在DSMC方法中，将粒子迁移运动视为直线运动，期间粒子不与其他粒子发生碰撞。所有仿真粒子迁移运动计算完成后，以主网格为单元选择粒子碰撞对，计算粒子间碰撞。为了确保碰撞对的选取是在最相邻的两个粒子之间进行的，DSMC方法将主网格再分为若干亚网格。同时，为了实现粒子运动与碰撞的解耦，计算的时间步长应远小于气体粒子的平均碰撞时间，并且为保证模拟粒子在亚网格内至少停留一个时间步长，亚网格的尺寸应与当地分子平均自由程相当。DSMC方法计算流程如图2所示。

粒子与壁面作用模型选择漫反射模型，壁面温度=300 K，反射分子的能量调节系数取1，为“完全热适应”。粒子间碰撞采用二元碰撞假设，即假定粒子间所有碰撞仅发生在两个粒子之间，不考虑多个粒子间碰撞。

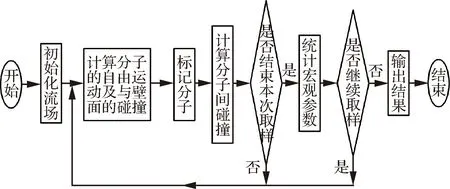
图2 DSMC计算流程图Fig.2 Computational flow chart of DSMC

2.2 程序验证

程序正确性验证见文献[27]，这里不再赘述。以下为针对本计算模型的程序独立性验证。计算模型参数设置为：=1，=5，=180°，即进气道末端壁面垂直于轴，飞行高度=120 km，来流特性参数见表1。依次验证了网格尺寸、时间步长()、初始时刻每个网格内的模拟粒子数(PPC)和取样次数()独立性，结果如图3所示。

图3(a)给出了当主网格参数×为30×30、60×60和90×90时，进气道中心线上的压力。代表轴方向网格数，代表轴方向网格数，且每个主网格又被分为4个亚网格。对于3套网格的网格尺寸，其所对应的亚网格尺寸均小于本文计算工况下(=120 km)粒子平均自由程的最小值，即0.015 m。结果显示3套网格尺寸下，进气道中心线压力基本一致。对于DSMC方法，主网格只作为统计流场宏观量的单元，其计算精度取决于主网格内模拟粒子的数量。选取主网格参数为30×30。

图3(b)对比了不同计算时间步长下，进气道中心线上的压力。为了保证一个时间步长内，粒子至少能在亚网格内停留一次，基于来流粒子的速度和亚网格尺寸，计算得=1.0×10s。结果表明，计算时间步长分别取0.1、和10时，进气道中心线压力基本一致。这是由于来流粒子进入进气道后，经粒子间碰撞以及粒子与壁面碰撞，粒子速度降低(小于1 000 m/s)，因此，计算步长取0.1和10同样也满足计算精度要求。在严格保证计算精度的前提下，同时考虑计算成本，计算时间步长取中间值。

图3(c)比较了初始时刻每个网格内的模拟粒子数(PPC)对中心线上压力计算结果的影响。PPC分别取10、20和30时，进气道中心线压力基本一致。这是由于本研究模拟的是一个粒子收集过程，随着数值计算的进行，每个主网格内模拟粒子数将逐渐增多，最终将远远大于DSMC方法要求的每个主网格内至少20～35个模拟粒子。在严格保证计算精度的前提下，同时考虑计算成本，PPC取中间值20。

图3 计算参数独立性验证Fig.3 Independence verification of calculated parameters

图3(d)为不同取样次数()下的中心线上压力计算结果。增加取样次数，进气道中心线上压力计算结果略有偏差。这是由于增加取样次数即增加计算时间，在时间推进过程中，新进入粒子与进气道内粒子的碰撞导致进气道内粒子向出口移动，气体压力进一步缓慢提高。当>200 000 时，每50 000次，压力提高幅度最大不超过2%。数值计算的收敛判据为：每10 000次，若压缩比满足-<0.1，收集效率满足-<0.01，认为计算已趋于收敛，流场达到稳定状态。保险起见，在此基础上再继续计算50 000次。

3 分子碰撞模型

DSMC分子间作用模型有：硬球模型(Hard Sphere Model, VH)、变径硬球模型(Variable Hard Sphere Model, VHS)、变径软球模型(Variable Soft Sphere Model, VSS)、广义硬球模型(Generalized Hard Sphere Model, GHS)和广义软球模型(Generalized Soft Sphere Model, GSS)等。其中，VH是最基础的分子间作用模型，VHS、VSS、GHS和GSS都是在VH的基础上，针对气体流动中存在的特殊问题而建立，目的是为了使数值仿真结果更接近实际气体流动结果。

对比VHS和VSS两种分子间作用模型对数值计算结果的影响，两种模型多用于模拟稀薄气体流，二者碰撞截面相同，碰撞后散射角不同：

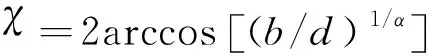
(1)

式中：为分子瞄准距离；为分子直径；VHS模型取=1，VSS模型取1<<2。

图4为分别采用VHS模型(=1)及VSS模型(1<<2)时，压缩比和收集效率的计算结果。计算模型参数为：=2，=10，=90°，=120 km。

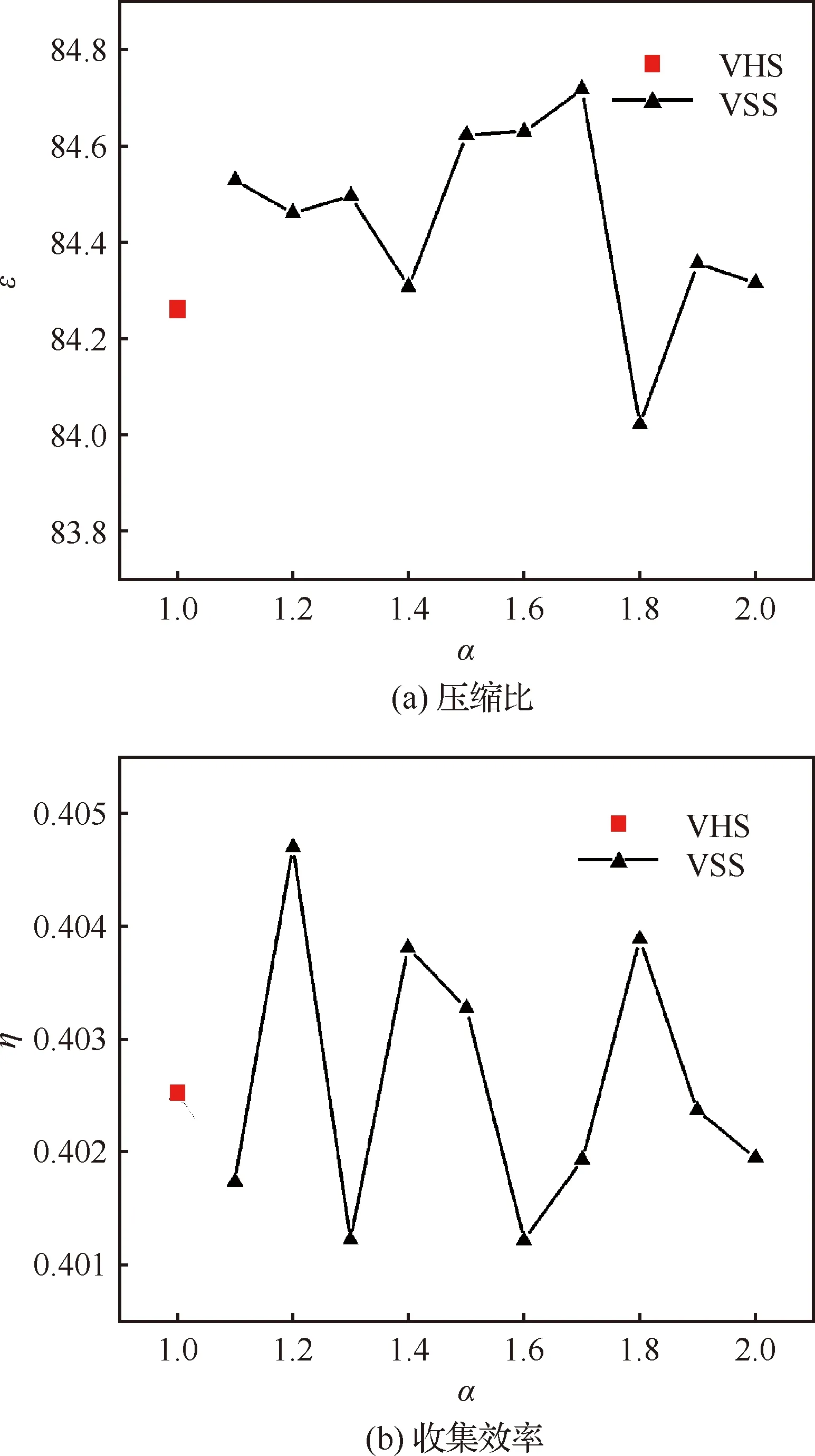
图4 不同α下进气道进气性能Fig.4 Intake performance of air-intake for different α

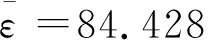
4 结果分析与讨论

4.1 进气道长纵比的影响

图5为不同进气道长纵比下的压缩比和收集效率。其中，=10，=90°，=120 km。

图5 不同Γ下进气道进气性能Fig.5 Intake performance of air-intake for differentΓ

随着的增大，和都呈现出先增大后逐渐稳定的变化趋势，且当=7时，和达到最大值。这是由于保持不变时，越小，进气道越短，大量被捕获的粒子未经与壁面的充分碰撞，仍具有较高的动能，从进气道入口离开的几率大，进气道出口粒子数密度较低，同时从进气道出口离开的粒子数较少，因此=和=较低。随着增大，进气道长度增加，进气道内粒子与壁面碰撞几率增加，动能降低，导致其从进气道入口离开的几率减小；另一方面，进气道内的低动能粒子受到新进入的高动能粒子的碰撞，使其向进气道出口方向运动，进气道出口粒子数密度增大，同时从进气道出口离开的粒子数增加，因此和逐渐增大。随着继续增大，进气道内粒子数密度继续增大，这导致新进入粒子与被捕获粒子的碰撞概率增加，同时由于进气道内的低动能粒子数逐渐增加，使得一些新进入的来流粒子没有足够的动能到达进气道出口，导致和的增长速度变缓。当大于7后，继续增大时，进气道内的低动能粒子数大大增加，新进入的高动能粒子对进气道内的低动能粒子的碰撞作用不足以支持进气道内粒子向进气道出口移动；另一方面，新进入粒子也由于进气道长度的增加，其动能降低的更多，无法顺利到达进气道出口，这两个因素都导致到达进气道出口的粒子数减少，因此，和开始逐渐减小。但是由于进入粒子基本不变，经过粒子间动量交换，能到达出口并从出口离开的粒子数亦基本不变，随着的增加，仅表现为聚集在进气道中部的粒子数增多。因此，和仅略微降低，当>7后，和曲线基本平直。

4.2 进气道出口锥角的影响

图6为不同进气道出口锥角下的压缩比和收集效率。其中，=2，=10，=120 km，从30°变化到180°，每个工况相差10°。

随着的增大，和都呈现出先增大后减小的变化趋势，不同的是，在=80°时达到最大值，在=60°时达到最大值。这是由于对于固定的和,越小，进气道有效空间越小，进气道捕集到的粒子数也相对较少，因此，当增大时，和也都逐渐增大；随着增大，一方面进气道有效空间提高；其次，来流粒子与锥形末端壁面发生碰撞后，粒子运动方向偏离进气道轴线方向，增加了粒子与进气道壁面的碰撞次数，降低了被捕获粒子从进气道入口离开的数量，因此，和分别达到最大值；随后，尽管继续增大，提高了进气道的有效空间，但由于进气道末端壁面逐渐趋于竖直，并最终垂直轴，即=180°，与进气道末端壁面碰撞的粒子，其运动方向与进气道轴线方向逐渐平行，粒子与进气道壁面的碰撞次数减少，增大，和降低。

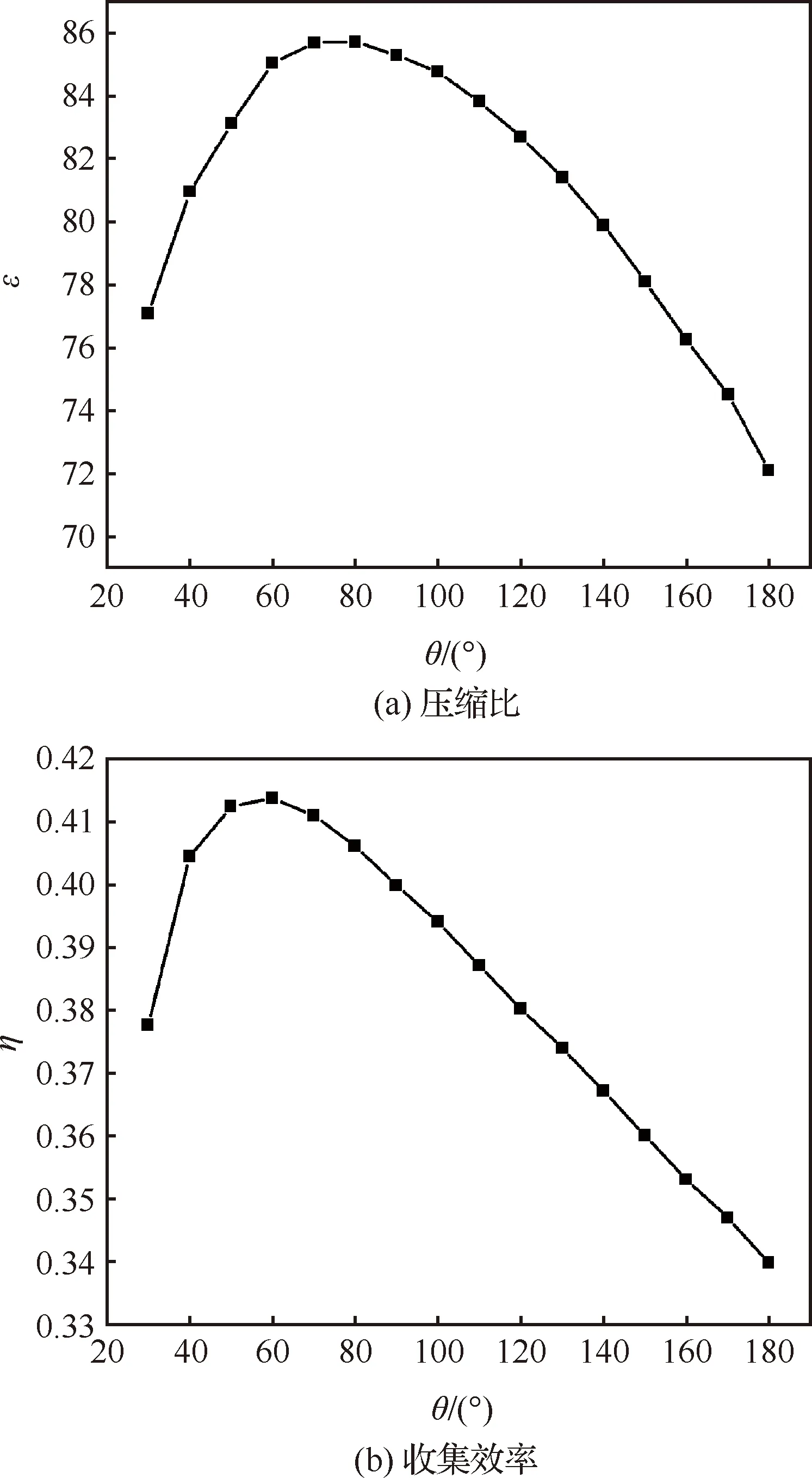
图6 不同θ下的进气道进气性能Fig.6 Intake performance of air-intake for different θ

4.3 栅格的影响

高马赫数来流气体基本平行于进气道轴线，当来流粒子进入进气道后，由于栅格的存在，粒子与固体壁面碰撞几率大大增加，导致粒子速度降低，方向偏离进气道轴线方向。同时，粒子速度方向偏离轴向，又增加了其与固体壁面的碰撞几率。此外，当被捕获粒子朝进气道入口运动时，栅格也能阻挡粒子从进气道入口逸出，从而提高进气道储存气体的能力。

图7为无栅格时和有栅格时，进气道内粒子数密度分布云图。其中，=2，=10，=90°，=120 km。栅格参数为：=4，=0.36 m，栅格板厚度=0.000 m。

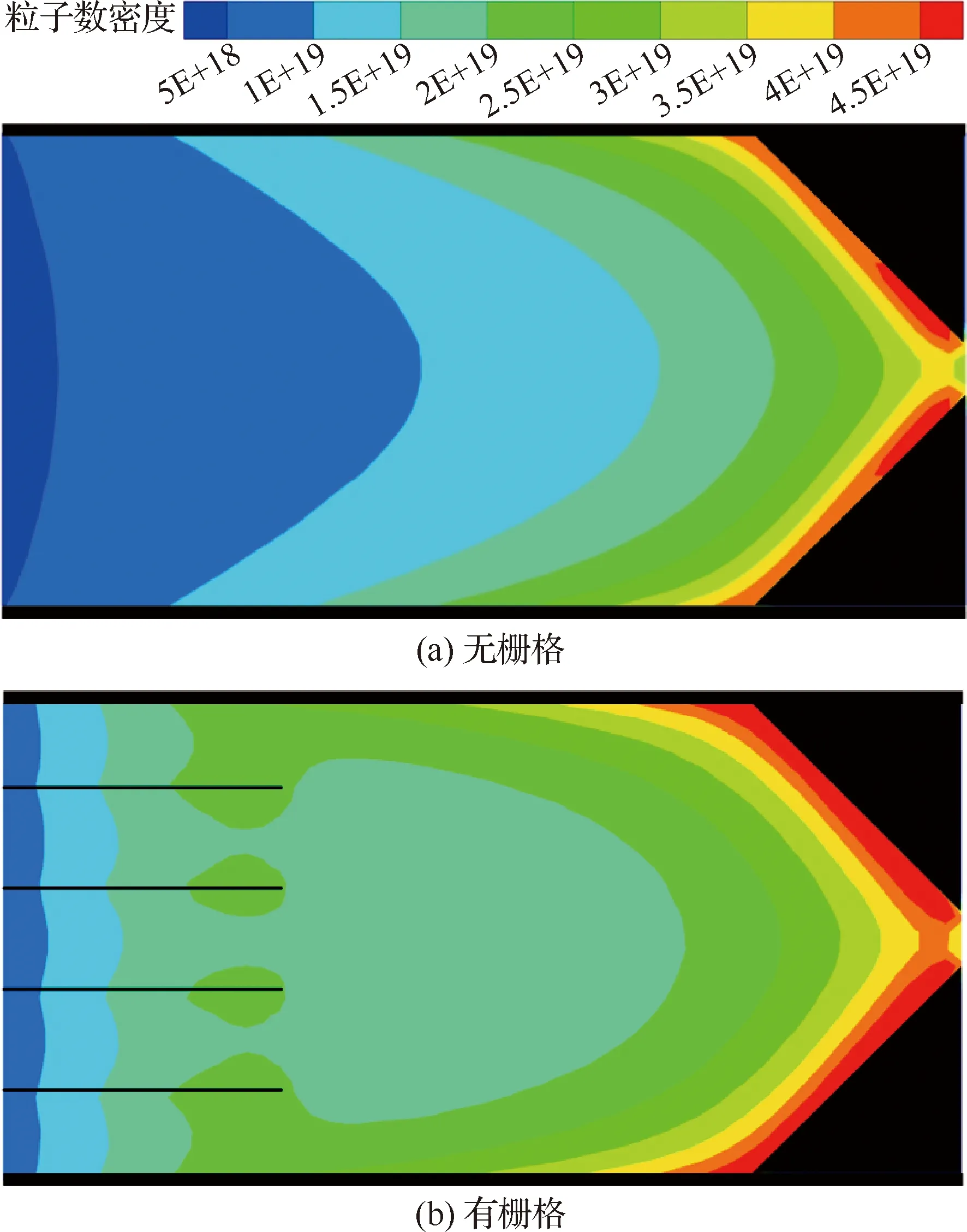
图7 进气道内粒子数密度云图Fig.7 Contour of particle number density in air-intake

对比图7(a)和图7(b)，可知，有栅格时的进气道内粒子数密度高于无栅格时。通过计算可得，无栅格时，=84.06，=0.399，有栅格时，=92.38，=0.403。

图8(a)和图8(b)分别给出了无栅格和有栅格时进气道内的某个特定粒子的运动轨迹。其中，蓝色细实线代表粒子运动轨迹，红色箭头代表粒子运动方向，黑色点代表粒子不同时刻位置，数字代表该粒子位置编号，此处设定每隔100记录一次粒子位置，期间若发生粒子间碰撞，也记录一次粒子的位置坐标。

从图8(a)可以看到，该粒子从进气道下部进入，经历多次与其他粒子的碰撞(轨迹线拐点处)及壁面碰撞，最终从进气道顶部逸出；设置栅格结构后，如图8(b)所示，该粒子进入进气道后，来回与栅格结构碰撞多次，期间该粒子与其他粒子碰撞及与壁面碰撞次数明显多于无栅格结构工况，动能大幅降低，在出口处，多次接近出口而最终返回进气道内部。因此，栅格的存在，粒子间碰撞及其与壁面碰撞的次数增加，其动能减小，逸出的概率减小，和提高。

图9(a)为不同栅格板厚度下，中心线上粒子数密度的沿程变化。其中，=2，=10，=90°，=4，=0.36 m，=120 km。同

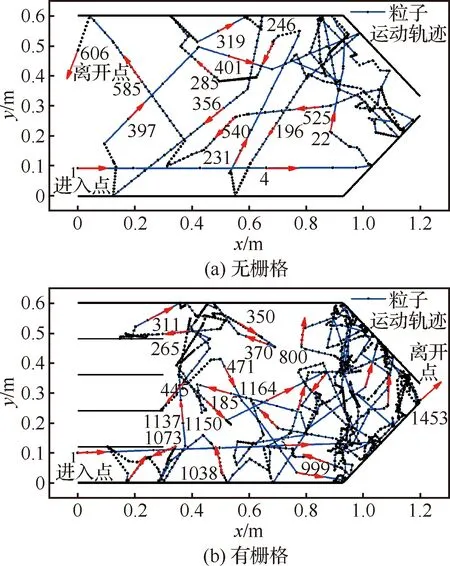
图8 进气道内粒子运动轨迹Fig.8 Trajectory of a particle in air-intake

时，由数值计算可得，=0 m时，=92.38，=0.403；=0.002 m时，=91.23，=0.404；=0.004 m时，=90.40，=0.408。因此，改变，对中心线上粒子数密度、和影响不大。这是由于栅格板厚度的增减，只影响了进气道入口的有效面积，对于粒子与栅格板上下壁面的碰撞没有影响。

图9(b)为不同栅格板层数下，中心线上粒子数密度的沿程变化。其中，=2，=10，=90°，=0 m，=0.36 m，=120 km。同时，由数值计算可得，=2时，=89.84，=0.411；=4时，=92.38，=0.403；=6时，=92.94，=0.391。发现增加，中心线上粒子数密度和提高，而降低。这是由于增加，一方面进气道内被捕获粒子与栅格固体壁面的碰撞次数增加，降低了粒子动能；其次，被捕获粒子从进气道入口逸出的概率降低，提高；之所以有少量降低，是由于越大，进气道内粒子数越多，导致粒子向进气道出口运动时，与其他粒子的碰撞次数增加，动能降低的更多，从出口离开的粒子数减少。

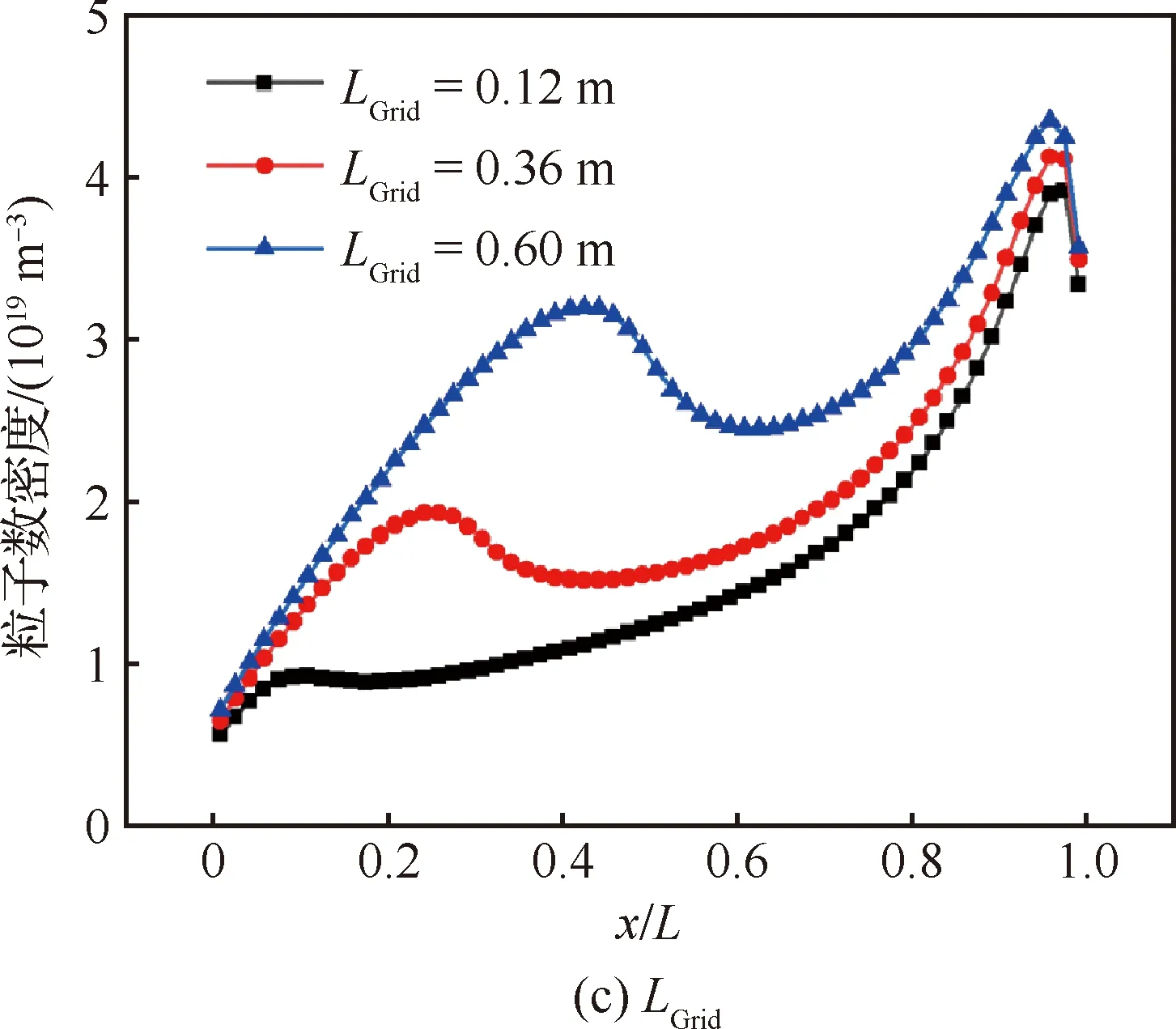
图9 不同栅格几何参数下沿进气道中心线粒子数密度变化Fig.9 Changes in particle number density along central line of air-intake for different grid geometry parameters

图9(c)为不同栅格板长度下，中心线上粒子数密度的沿程变化。其中，=2，=10，=90°，=0 m，=4，=120 km。由数值计算可得，=0.12 m时，=89.67，=0.417；=0.36 m时，=92.38，=0.403；=0.60 m时，=93.90，=0.389。发现增加与增加对中心线上粒子数密度、和的影响大致相同，区别在于增加时，降低的幅度更大。这是由于增加时，进气道内粒子数密度增加的幅度更大，粒子向进气道出口移动时动能降低的也相对更多，从出口离开的粒子数()也更少。

5 结 论

1) 在一定范围内，提高进气道长纵比，可以提高压缩比和收集效率，继续提高进气道长纵比，压缩比和收集效率将不再增加，并最终保持稳定。

2) 增大进气道出口锥角，压缩比和收集效率呈现出先增大后减小的变化趋势，出口锥角存在最优值，此时压缩比和收集效率最大。

3) 栅格结构有助于粒子间及粒子与壁面间的碰撞，有效防止已捕获粒子从进口逸出，从而提高进气道压缩比和收集效率；一定范围内，增加栅格板长度和栅格板层数，压缩比随之升高，但收集效率降低。