三段式Halbach阵列永磁电机解析建模与研究

杨明磊,钟再敏,邵仲书,陈辛波

(同济大学汽车学院,201804,上海)

分块Halbach阵列永磁体是由若干个充磁方向不同的永磁体按照一定的规律排列组成,与传统永磁体结构相比,分块Halbach阵列永磁体生成的气隙磁场谐波含量更少[1-2]。同时,因为分块Halbach阵列永磁体具有单边聚磁的特点,所以其气隙侧的磁通密度更高,能有效地提高转矩密度[3-4]。分块Halbach阵列永磁电机成为目前高精度伺服控制领域的研究热点。

理论上Halbach永磁体的每极分块数越多,其气隙磁场的正弦性越好,但是考虑到工程实现难度和性能提升效果,每极分3块,即三段式Halbach阵列永磁体结构最为适合[5-6]。对于三段式Halbach永磁电机来说,目前没有一个明确的理论设计公式,所以在初始设计阶段,需要借助合适的磁场分析方法来分析结构参数对电机电磁性能的影响规律。常用的电机磁场分析方法有有限元法和解析法,其中有限元法能够考虑损耗和磁饱和,具有很高的计算精度,但是对于分块Halbach阵列这种具有复杂充磁结构的电机来说,有限元建模复杂且计算时间长,并不适用于电机的初始设计和优化[7-8]。

解析法是近年来常用的电机磁场快速计算方法,可以从理论层面上明确设计参数与电磁性能之间的关系。同时,解析法可以快速调整电机的结构参数,十分便于分块Halbach阵列永磁电机的初始设计和电磁性能规律研究[9]。目前解析法有保角变换法[10-12]、子域模型法[13-21]和多层建模法[22-30]。保角变换法利用气隙磁导函数可以快速求得开槽电机的磁场分布情况,是最早的一种解析方法。罗玲等[12]利用保角变化,分析了不同磁极分块数和不同充磁夹角对电机转矩的影响,但因为无法考虑实际槽深,以致保角变换法计算精度较低。基于麦克斯韦方程组,子域模型法将复杂的电机结构在二维的平面内划分为若干个子域,可以考虑槽开口结构、定子槽型和永磁体拓扑结构。张河山等[17]利用子域模型法,建立了分块Halbach阵列永磁电机的解析模型,研究了每极分块数对电机电磁性能的影响规律,但是所提模型磁极分块宽度相同,且充磁夹角不能任意改变。高锋阳等[18]提出了不等宽不等厚三段式Halbach阵列永磁电机,研究了不同Halbach拓扑结构对电磁性能的影响规律,但是并没有考虑充磁夹角变化的影响。此外子域模型法也在分块Halbach阵列轴向磁通电机[15-16]、分块Halbach阵列直线电机[13]、Halbach阵列双转子电机[20]和考虑转子偏心的Halbach阵列永磁电机[21]的磁场解析计算上得到了广泛的应用。但是,子域模型法需要假设电机内部所有的软磁材料磁导率为无穷大,这导致其初始设计和优化结果的可信度有限。鉴于子域模型不能考虑材料磁导率的缺陷,Sprangers等[22]提出了多层建模方法,该方法根据激励源和介质的不同,将电机沿径向划分成多层,并利用柯西乘积,将每一层中的磁导率分布特点考虑到磁场求解中。研究学者们基于多层解析建模的方法,建立了同步磁阻电机[23]、表贴式永磁电机[24]、磁通调制永磁电机[25]和双转子永磁电机[30]的解析模型,考虑软磁材料相对磁导率为固定值,分析了不同类型电机的电磁性能以及结构参数变化对电磁性能的影响规律。研究结果表明,考虑材料磁导率的多层解析模型具有很好的计算精度。同时,多层建模法通过结合一些迭代算法,能够考虑软磁材料的非线性变化,进一步提高解析计算精度[26-29],但是迭代算法的引入大大增加了计算时间,不适用于初始设计和优化。目前还没有研究将多层建模的方法用于三段式Halbach阵列永磁电机的磁场分析上。

本文基于多层建模的方法,建立了考虑软磁材料磁导率为具体值的三段式Halbach阵列永磁电机的多层解析模型。该解析模型考虑了槽开口结构和实际槽深,而且能够描述不同磁极宽度和不同充磁夹角等复杂拓扑结构,同时考虑软磁材料的磁导率使得解析计算结果更加准确可信。基于该模型,本文分析计算了三段式Halbach永磁电机的空载和负载工况下的气隙磁密、磁链、反电动势和转矩等电磁性能,并通过与有限元模型计算结果对比,验证了多层解析模型的正确性和准确性。最后,利用所提出的多层解析模型,研究了槽开口宽度、磁极宽度和充磁夹角对三段式Halbach阵列永磁电机输出转矩的影响规律,并根据分析结果给出了输出转矩最优的设计方案。

1 三段式Halbach电机模型

三段式Halbach阵列永磁电机的结构简图如图1所示,为了便于描述电机的多层模型结构将电机在二维极坐标系中展开。根据激励源和磁介质的不同,将电机划分为Halbach阵列永磁体层(Ⅰ)、气隙层(Ⅱ)、定子齿尖层(Ⅲ)和电枢绕组层(Ⅳ)4层。在图1(b)中,R1、Rm、Rs、Rc和Ry分别是转子轭外表面半径、永磁体表面半径、定子齿顶表面半径、定子槽内半径和定子槽底半径;θct、θcs、θt和θs分别是定子齿尖宽度、槽开口宽度、定子齿宽和定子槽宽;Ji,left、Ji,right分别为第i个槽内的左侧、右侧电流密度。三段式Halbach阵列永磁体的结构简图如图2所示,每极永磁体由两块宽度为θ1的副磁极和一块宽度为θ2的主磁极构成,主磁极的充磁方式为径向充磁,副磁极充磁方向与主磁极充磁方向的夹角为θm。

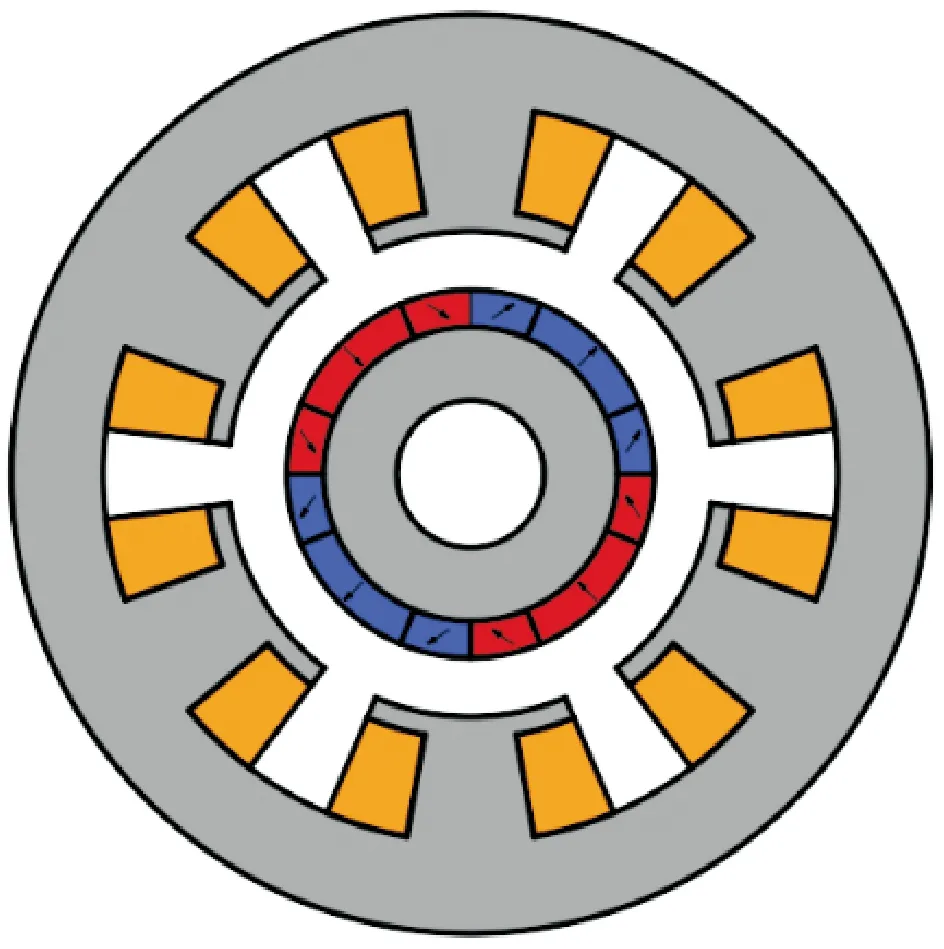
(a)三段式Halbach阵列永磁电机的横截面

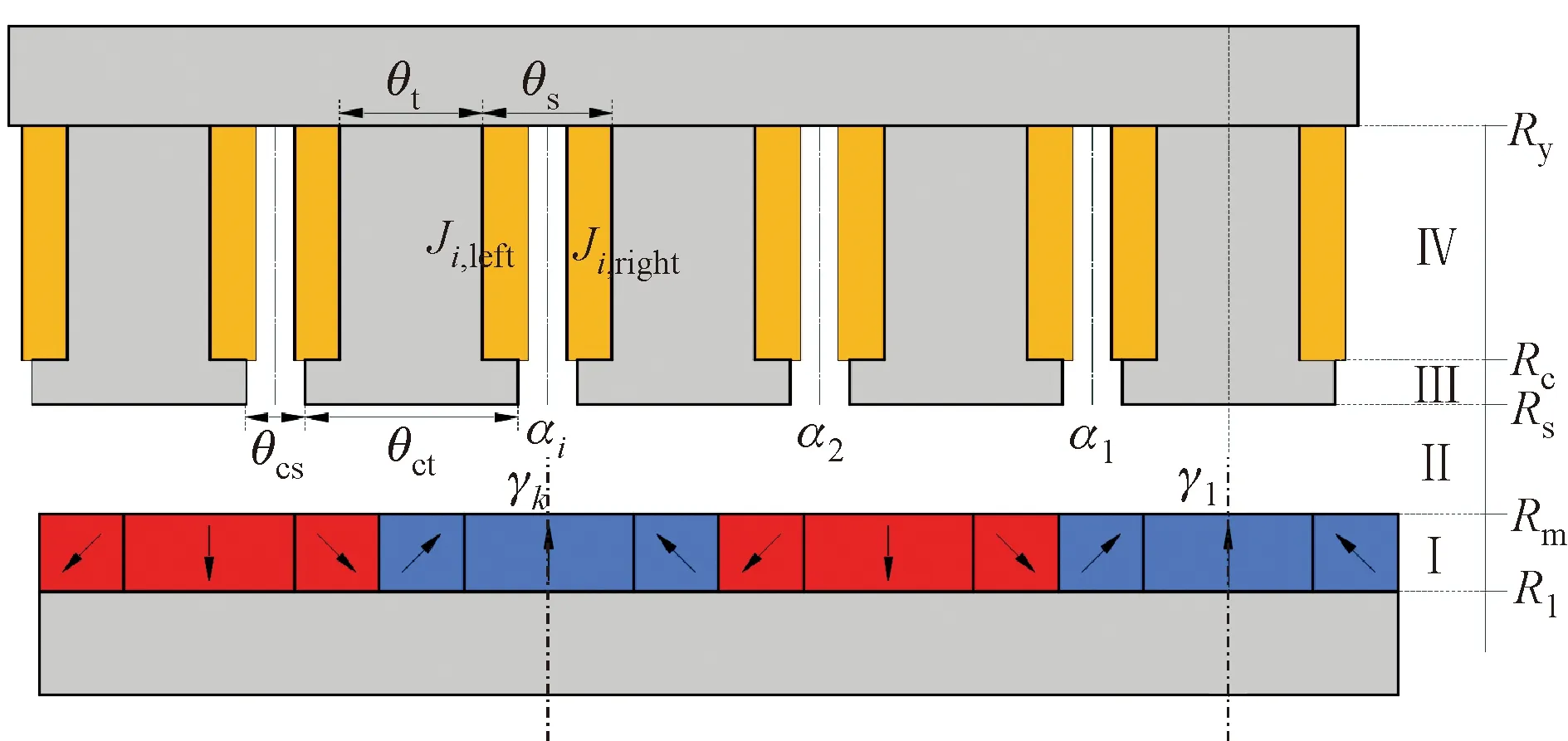
(b)电机在二维极坐标系中的展开图

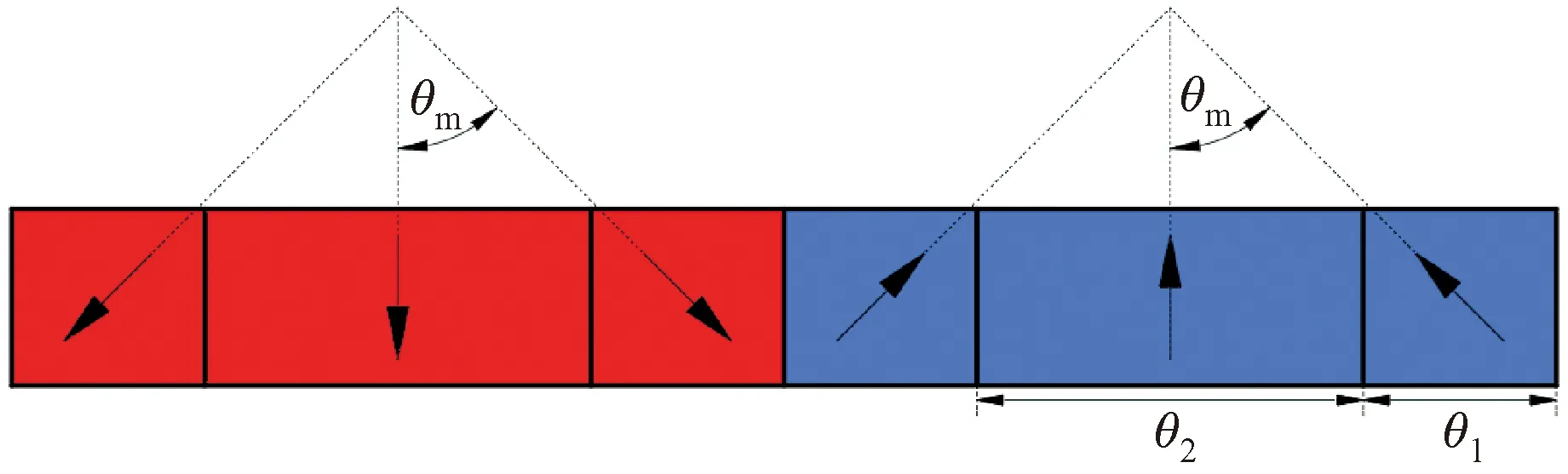
图2 三段式Halbach阵列永磁体结构简图Fig.2 Structure diagram of three-segment Halbach array permanent magnet

为了简化多层模型,忽略了电机的涡流效应和端部效应;假设定子齿部软磁材料的磁导率为固定值;假设转子轭和定子轭的相对磁导率为无穷大。

为了进一步描述三段式Halbach阵列永磁电机的多层解析模型,规定第i个槽开口的位置为αi,第k个N极Halbach主磁极的位置为γk,两个参数分别可以表示成

(1)

(2)

式中:Qs为定子齿数;p为极对数;φ为第一个N极Halbach主磁极与第一个槽开口位置之间的夹角。

2 电流密度和Halbach阵列永磁体

三段式Halbach阵列永磁电机内的激励源有两类,分别是电枢绕组层中的电枢电流和永磁体层中的Halbach阵列永磁体。

2.1 电枢电流分布

如图1所示,定子采用双层绕组形式,左右两个线圈的电流密度分布可以表示成

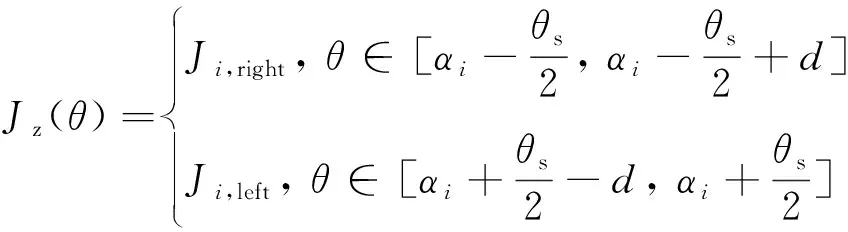
(3)

其中Ji,left、Ji,right可以表示为

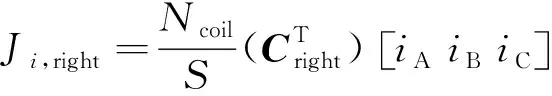
(4)

(5)

式中:Ncoil为每相串联总匝数;Cleft和Cright分别为电枢槽左右绕组的分布矩阵;S为单侧绕组截面积,可以表示成

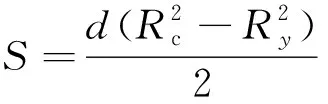
(6)

式中,d为单侧绕组宽度。

电流源为周期性分布,可以表示成复数形式的傅里叶级数[22]

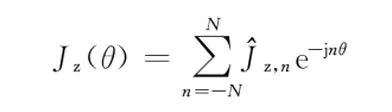
(7)

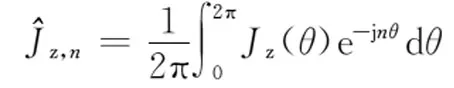
(8)

2.2 三段式Halbach阵列永磁体分布

三段式Halbach阵列永磁体的磁化强度在二维极坐标系中可以分解为径向和切向两个分量。根据图2中定义的每块永磁体的充磁方向,三段式Halbach阵列永磁体在0～2π圆周上径向磁化强度Mr(θ)和切向磁化强度Mθ(θ)的分布可以表示为

Mr(θ)=

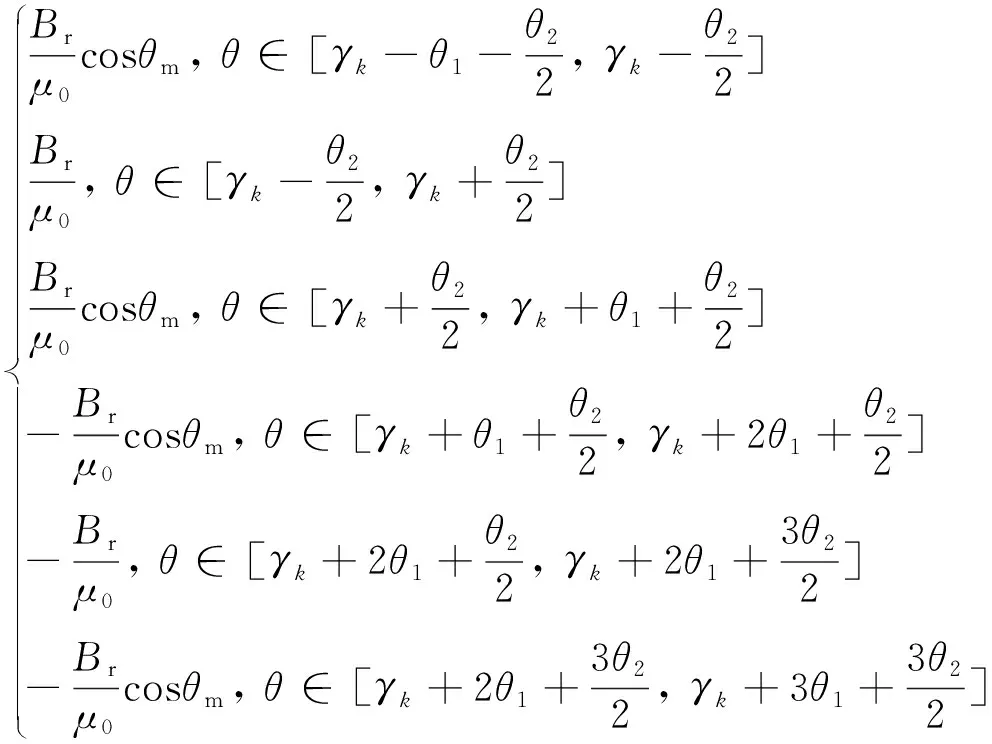
(9)

Mθ(θ)=

(10)

周期性分布的磁化强度分量也可以表示成复数形式的傅里叶级数

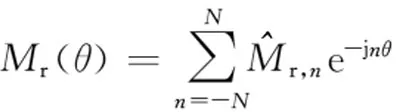
(11)

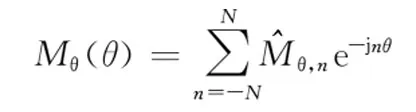
(12)

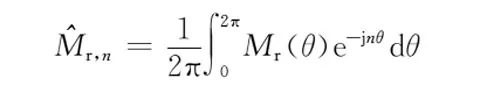
(13)

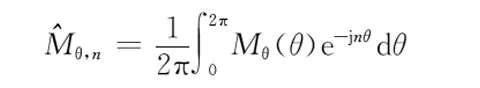
(14)

3 磁导率分布

如图1所示,4类磁场求解层的磁介质圆周分布不同,Ⅰ层的磁介质为永磁体, 则μⅠ(θ)=μmμ0。Ⅱ层的磁介质为空气,则μⅡ(θ)=μ0。Ⅲ层和Ⅳ层的磁介质有空气和铁心两类,其圆周上的分布为

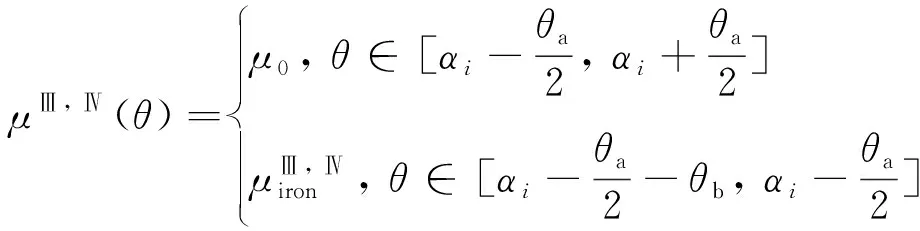
(15)

式中:对于Ⅲ层来说,θb为θt1,θa为θs1,对于Ⅳ层来说θb为θt,θa为θs。

圆周上Ⅲ和Ⅳ层磁介质磁导率的复数形式的傅里叶级数可以表示为[22]

(16)

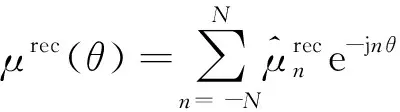
(17)

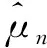
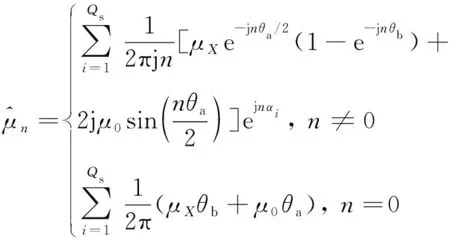
(18)

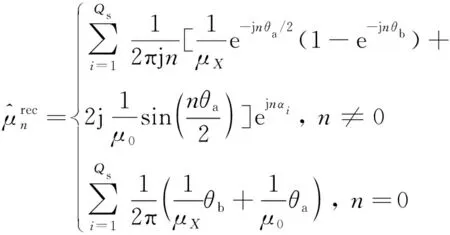
(19)

除了气隙层和三段式Halbach阵列永磁层之外,其他求解层中的磁导率切向方向不连续。因此,利用柯西乘积定理,B和H的关系用矩阵形式表示为[30]

Br=μc,rHr+μ0Mr

(20)

Bθ=μc,θHθ+μ0Mθ

(21)

磁导率的径向和切向分量的卷积矩阵可以表示为[22]

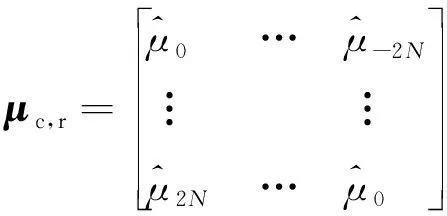
(22)

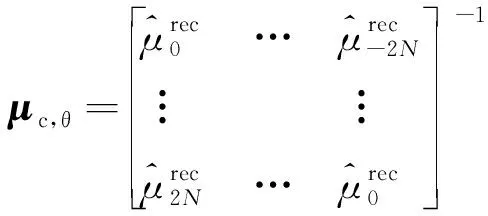
(23)

4 多层解析建模

4.1 磁矢位求解

基于麦克斯韦方程组、安培环路定理以及式(20)和式(21),可以写出4类磁场求解层的磁矢位求解方程。对于没有激励源的求解层来说,磁矢位求解方程为拉普拉斯方程,对于存在电流激励源或永磁体激励源的求解层,磁矢位求解方程为泊松方程

(24)

式中

V2=μc,θK[μc,r]-1K

(25)

K=diag(-N, …, -1, 1, …,N)

(26)

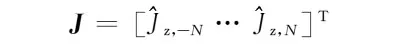
(27)

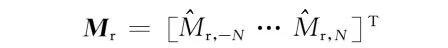
(28)

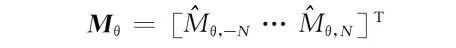
(29)

根据式(24),可以求解出4类求解层的磁矢位

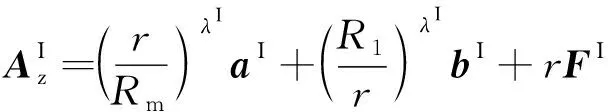
(30)

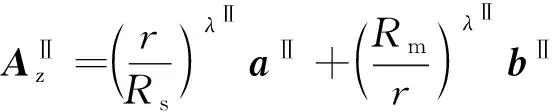
(31)

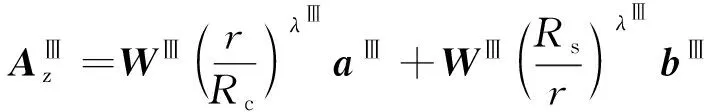
(32)

(33)

式中:WⅢ,Ⅳ和λⅢ,Ⅳ分别是矩阵VⅢ,Ⅳ的特征值矩阵和特征向量矩阵;λⅠ,Ⅱ=|K|;a和b为待求解系数;FⅠ,Ⅳ分别为Ⅰ和Ⅳ泊松方程的特解

FⅠ=-μ0(I-K2)-1(jKMr+Mθ)

(34)

(35)

其中,I是大小与K相同的单位矩阵。

4.2 边界条件

为了计算各求解层磁矢位中的待求解系数a和b,需要借助边界条件。第一类边界条件是:相邻求解层交界面(r=Rm、Rs或Rc)处的径向磁通和切向磁场相等,如下式

在Halbach阵列永磁体表面处(r=Rm)

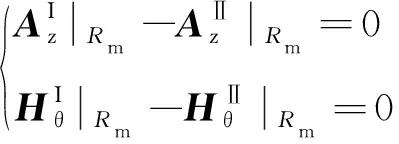
(36)

在定子齿顶表面处(r=Rs)

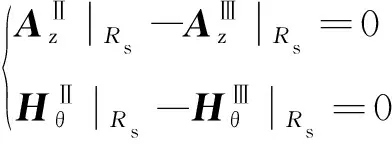
(37)

在定子槽顶表面处(r=Rc)

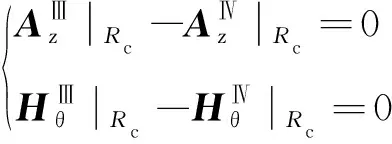
(38)

第二类边界条件是:根据转子轭和定子轭的相对磁导率为无穷大的假设,在内转子轭外表面和定子轭内表面(r=R1和r=Ry)处的磁场强度为0,如下式

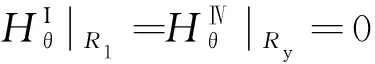
(39)

根据8个边界条件,可以求得各磁场求解层通解中的谐波系数(求解矩阵见附录A的公式A1)。

5 电磁性能计算与对比

为验证上述解析模型的正确性,对一台24槽20极的三段式Halbach阵列永磁电机进行建模和解析计算。电机的主要参数见表1,采用分数槽集中绕组形式(绕组展开图以及绕组分布矩阵Cright和Cleft见附录B)。

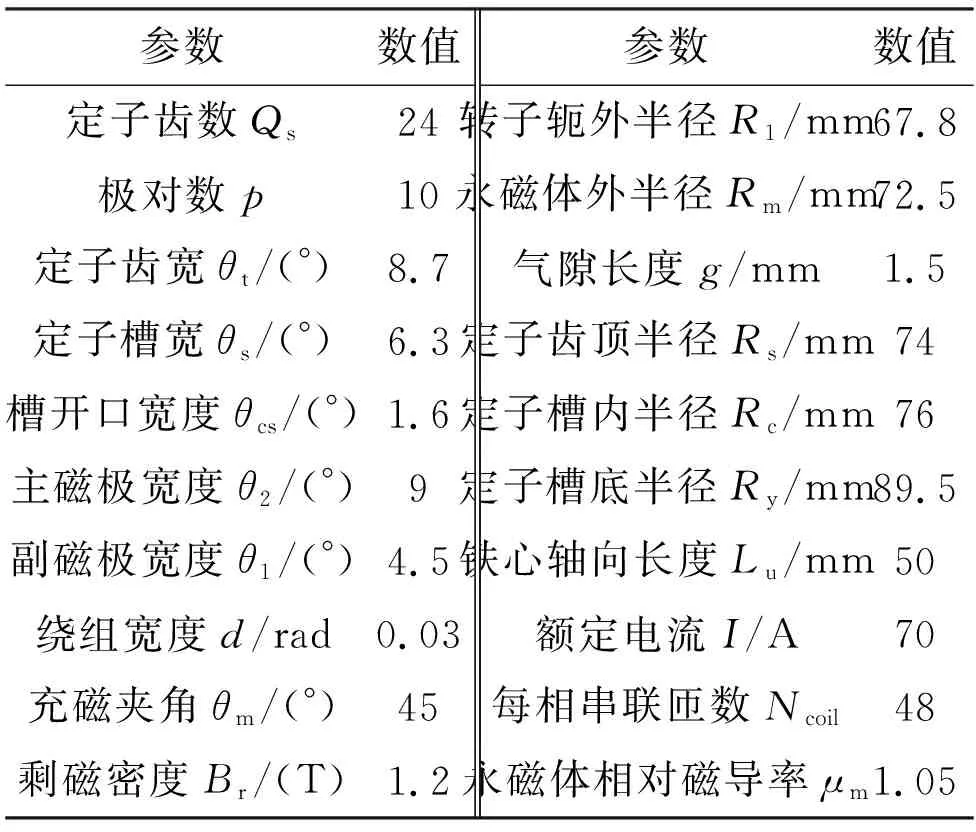
表1 电机主要参数

为了验证多层解析模型的正确性,在Maxwell软件中建立了电机的2D有限元模型,有限元模型中定子铁心相对磁导率的设置与多层模型一致,即有限元模型中定子铁心的相对磁导率为固定值300。图3给出了负载电流为70 A时的二维有限元模型的仿真结果。为了保证有限元模型的计算精度,将气隙划分成4层,总的网格数为31 756。利用该有限元模型可以验证多层解析模型的正确性。

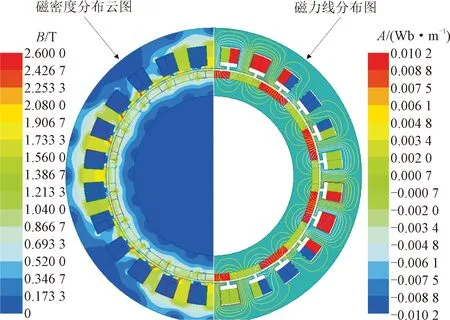
图3 负载电流为70 A时二维有限元模型的仿真结果Fig.3 Simulation results of the 2D finite element model at the load current of 70 A

5.1 空载电磁性能

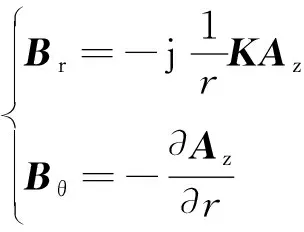
(40)

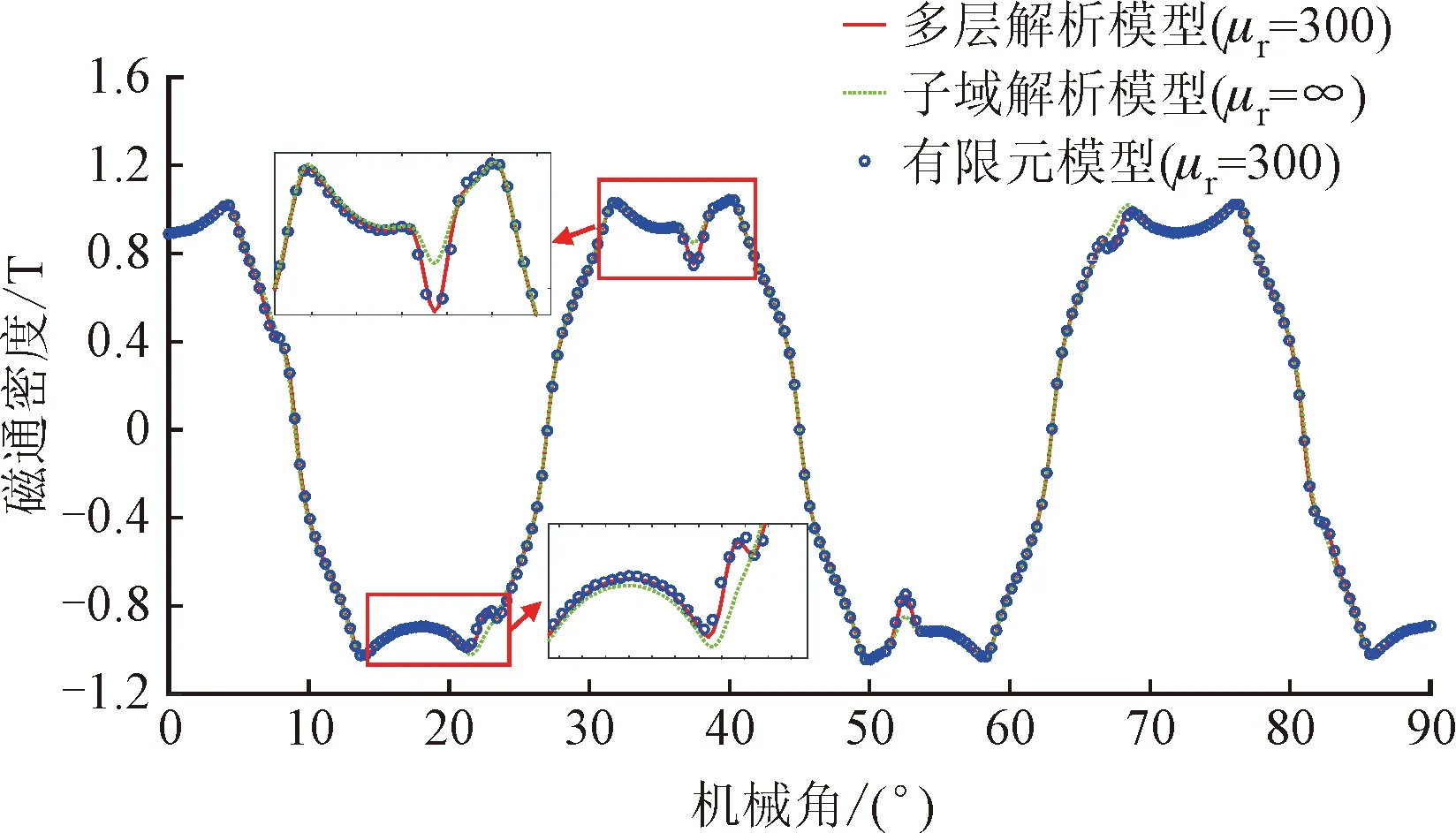
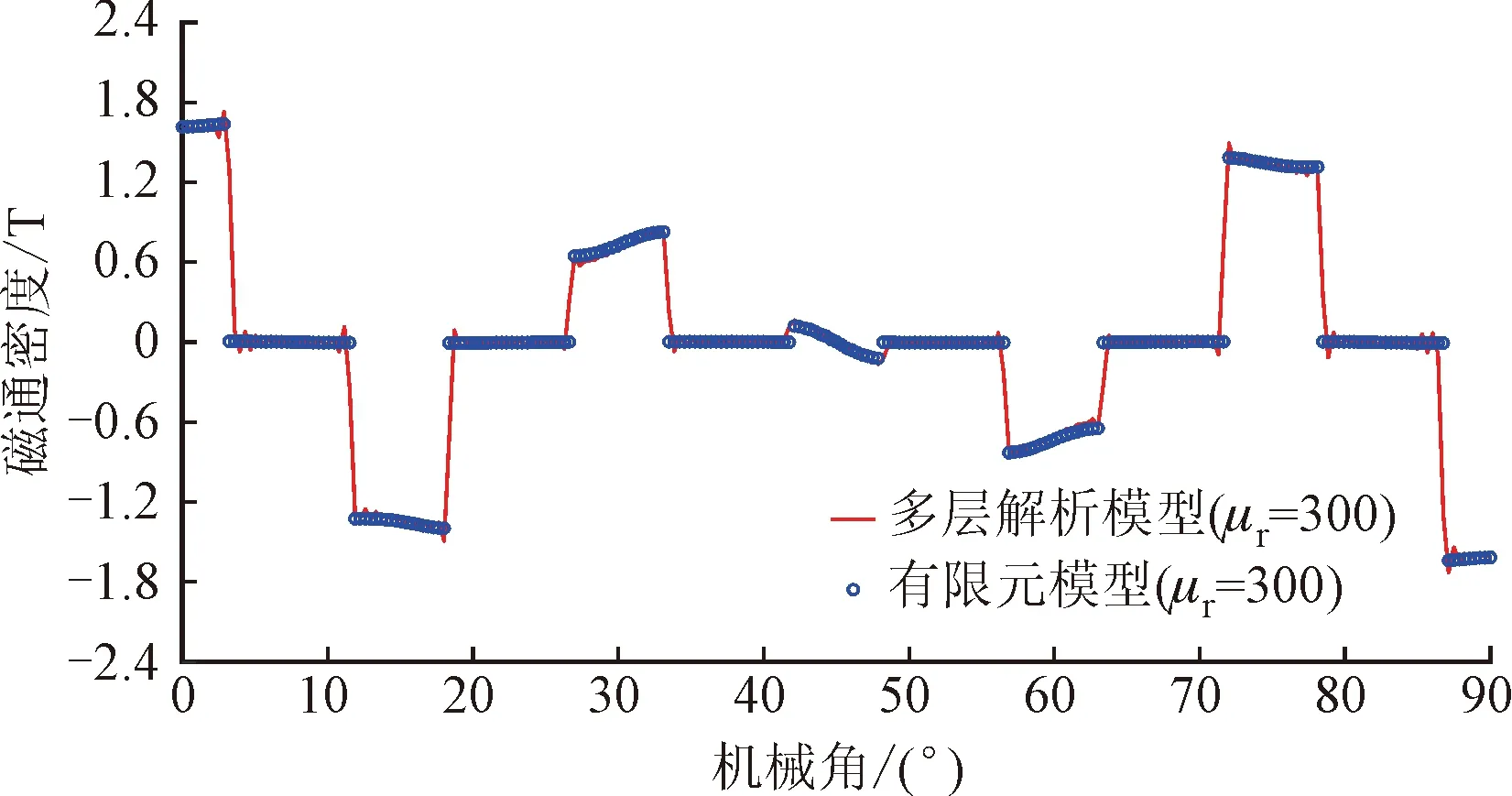
图4为气隙中间位置磁通密度的多层模型、子域模型和有限元模型计算结果的对比,由图4可以看出,多层解析模型的计算结果跟有限元模型计算结果基本一致,证明了多层解析模型的正确性。假设铁心材料相对磁导率为无穷大的传统子域模型,计算结果与有限元模型和多层解析模型的结果有一定的偏差。

(a)径向分量

(b)切向分量

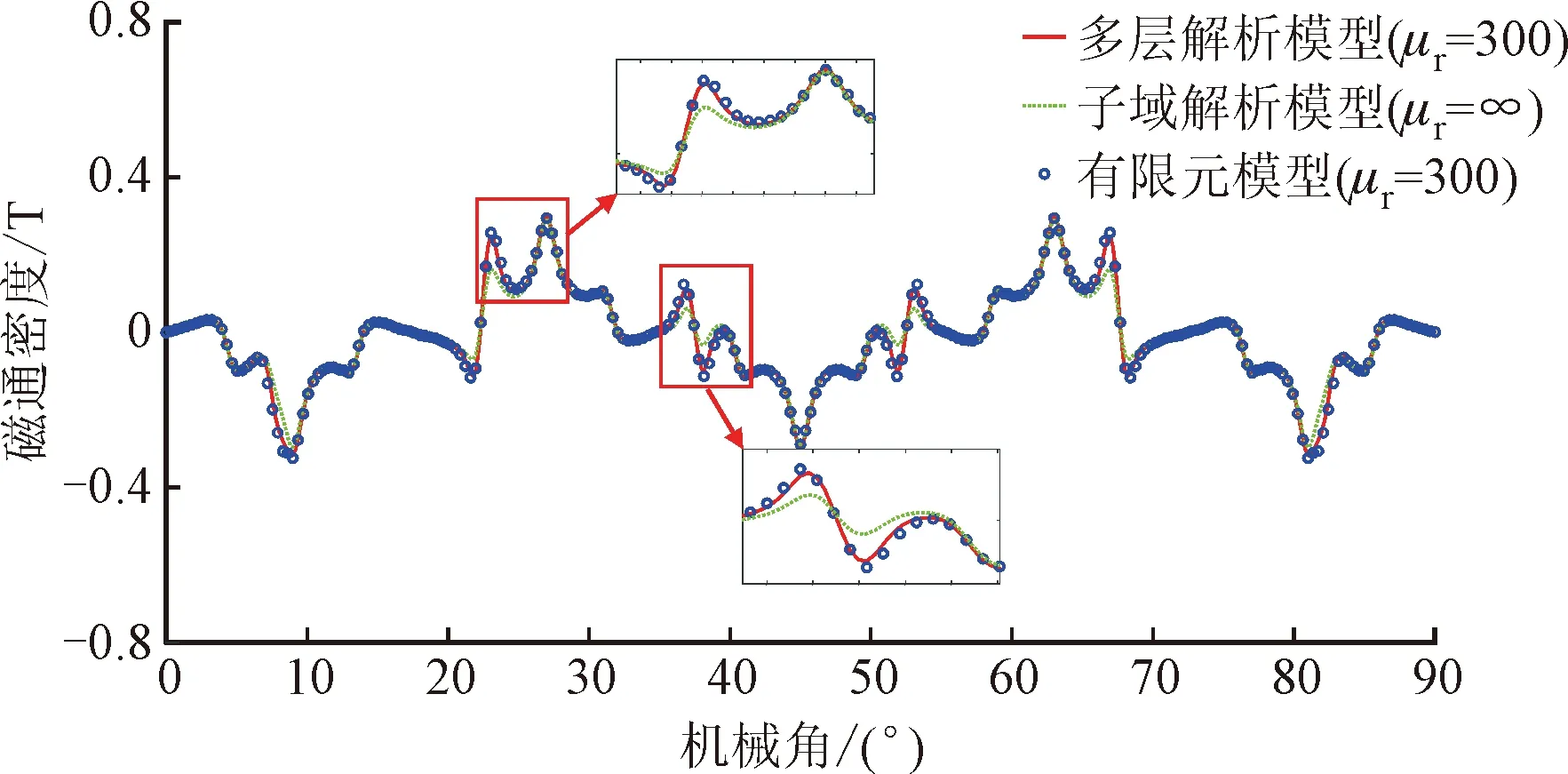
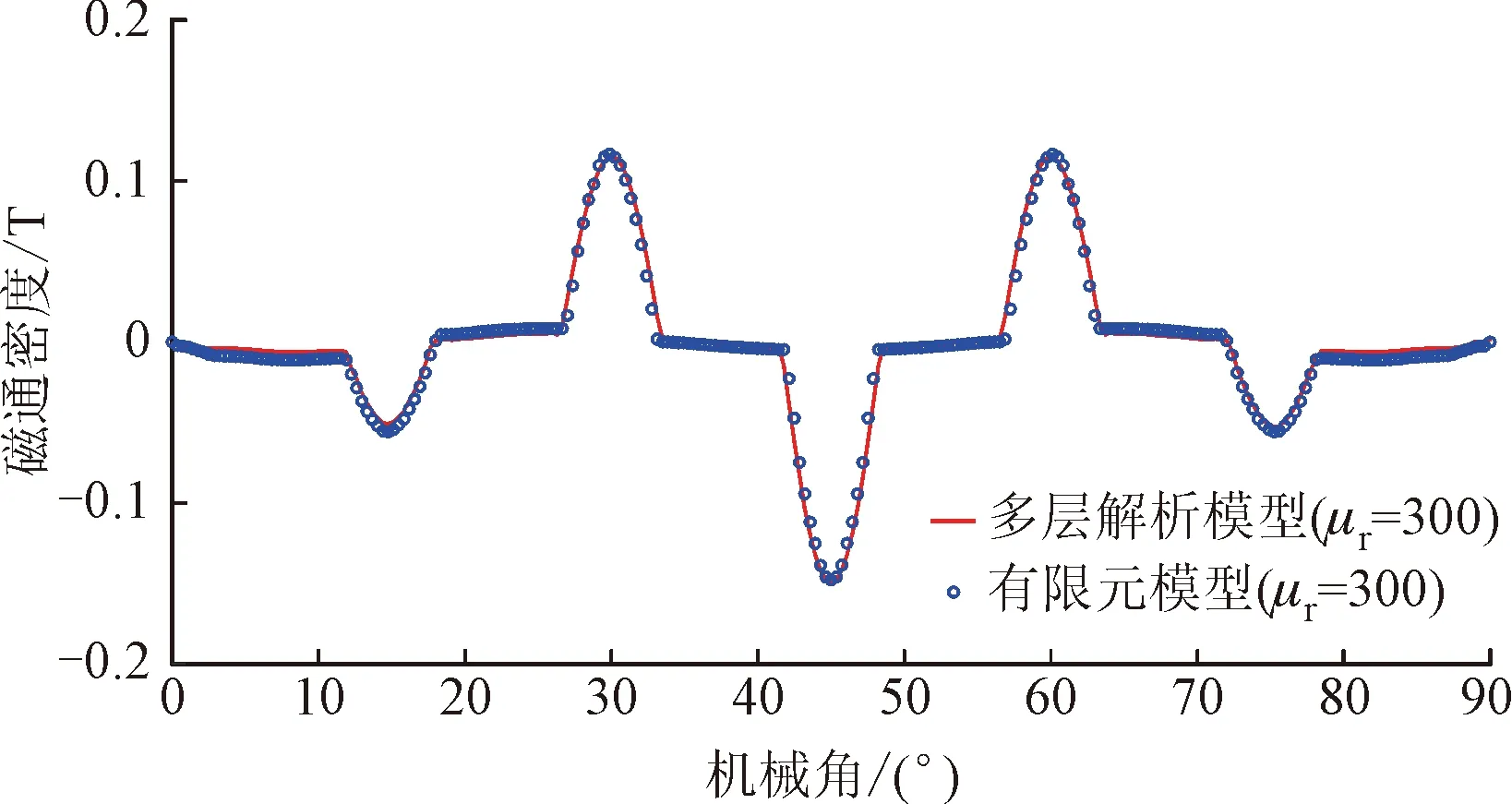
图5为空载工况下电枢绕组层(区域Ⅳ)平均半径处的磁感应强度径向和切向分布曲线对比。可以看出,多层解析模型计算得到的磁场分布结果与有限元模型计算结果吻合得很好。但是,假设定子铁心的相对磁导率为无穷大,子域模型无法求解出包含定子铁心的电枢绕组层在圆周上的磁感应强度分布曲线。

(a)径向分量

(b)切向分量

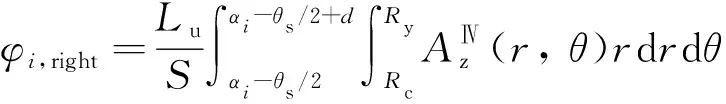
(41)

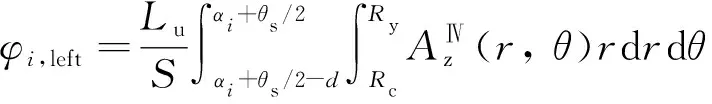
(42)

式中,Lu为铁心轴向长度。

定子绕组的三相磁链可以表示为

(43)

图6是电机在转速为2 000 r/min下空载磁链的多层模型解析计算结果与有限元模型计算结果、子域模型计算结果的对比。可以看出,多层解析模型和有限元模型的计算结果基本一致,证明了多层解析模型的正确性。忽略铁心软磁材料磁阻的子域模型的计算结果偏大。

图6 转速为2 000 r/min时的空载磁链Fig.6 No-load flux linkage at 2 000 r/min

通过对磁链的求导可以得到反电动势,计算公式为

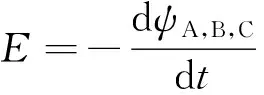
(44)

图7是3种模型在电机转速2 000 r/min时计算得到的空载反电动势对比,可以看出,3种计算结果得到的空载反电动势趋势相同。考虑铁心材料磁导率的多层解析模型和有限元模型计算到的空载反电动势峰值分别为66.08 V和65.57 V,两者相差0.51 V,相对误差小于1%,证明了多层解析模型的正确性。子域模型计算得到的空载反电动势峰值为69.73 V,忽略软磁材料磁阻的子域模型计算结果偏大。

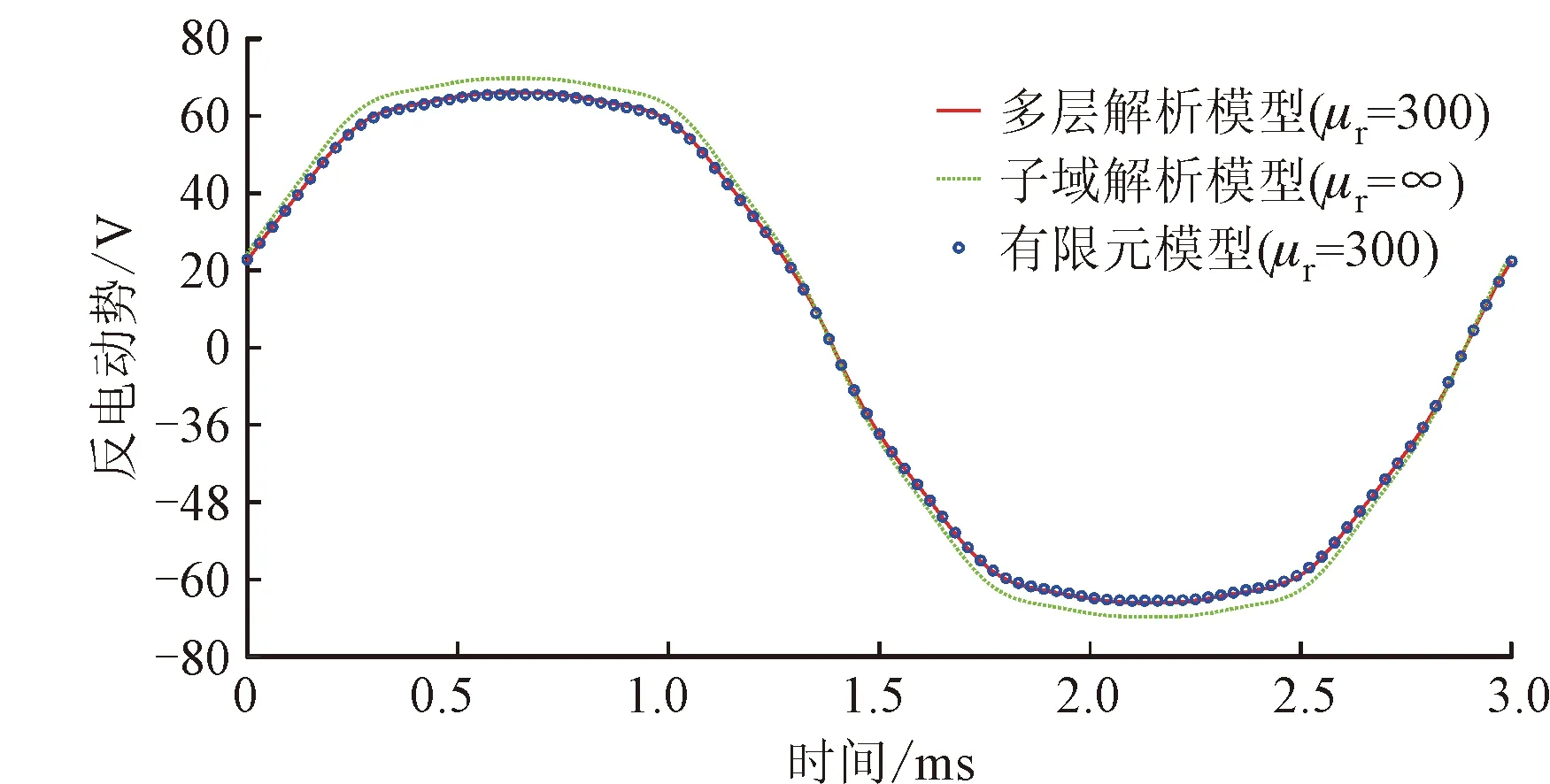
图7 转速为2 000 r/min时的空载反电动势Fig.7 No-load back EMF at 2 000 r/min

基于麦克斯韦应力张量法,利用计算得到的气隙磁通密度来计算电机的转矩

(45)

在空载工况下,式(45)计算得到的是齿槽转矩。图8是两种解析模型与有限元模型齿槽转矩计算结果的对比。可以看出,多层解析模型与有限元模型的齿槽转矩曲线吻合得很好,两者结果误差只有41.58 mN·m。由于忽略了定子铁心的磁阻,子域模型计算得到的齿槽转矩严重偏小。

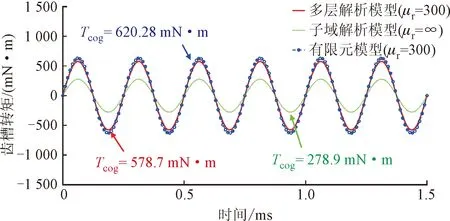
图8 两种解析模型与有限元模型齿槽转矩计算结果的对比Fig.8 Comparison of the results of cogging torque calculations for two analytical models and FEM

5.2 负载电磁性能

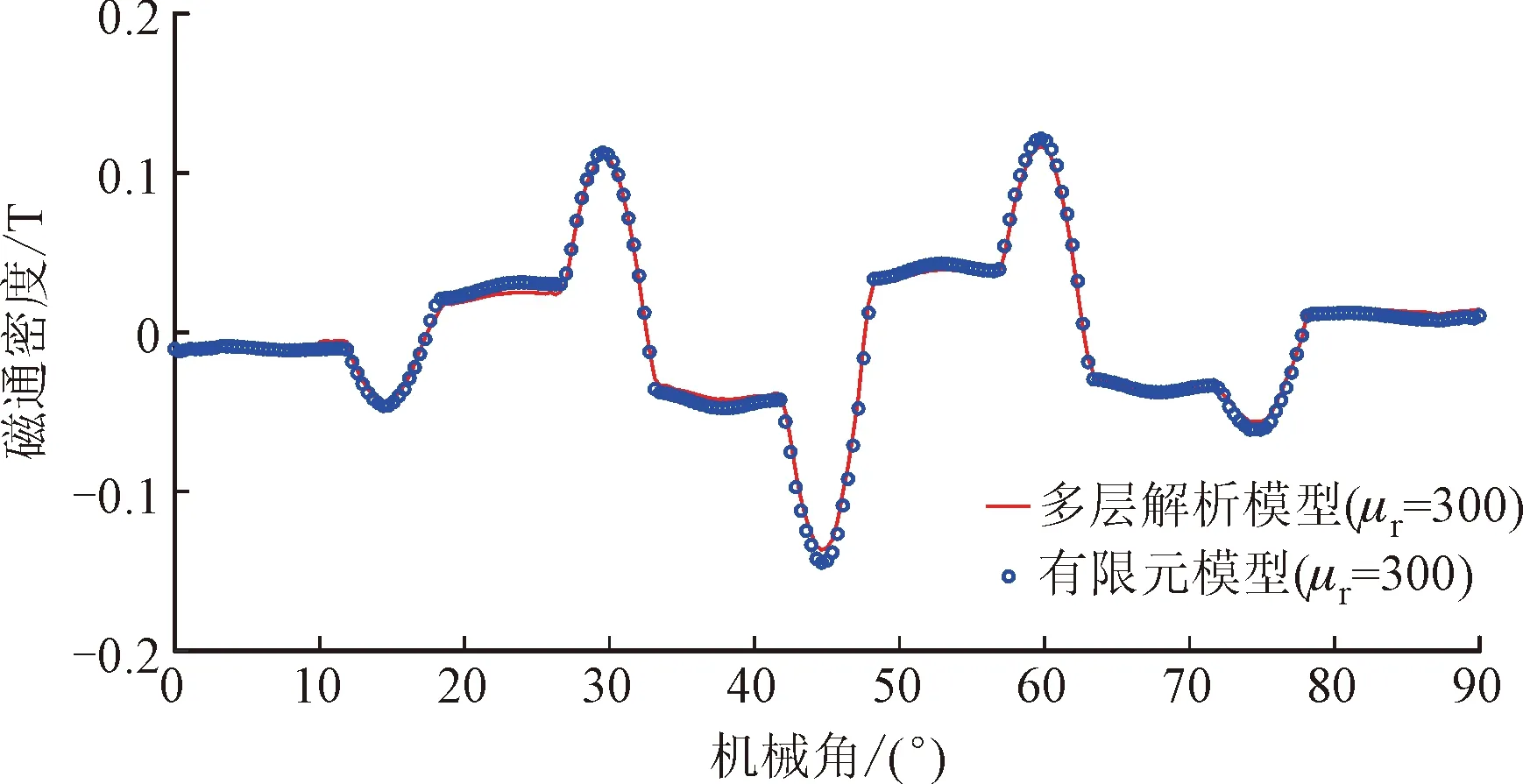
当励磁电流I=70 A时,气隙中间位置处的磁通密度分布的对比如图9所示。可以看出相比于子域模型,考虑材料磁导率的多层解析模型的计算结果与有限元模型的计算结果吻合得很好,进一步证明了多层解析模型的正确性。

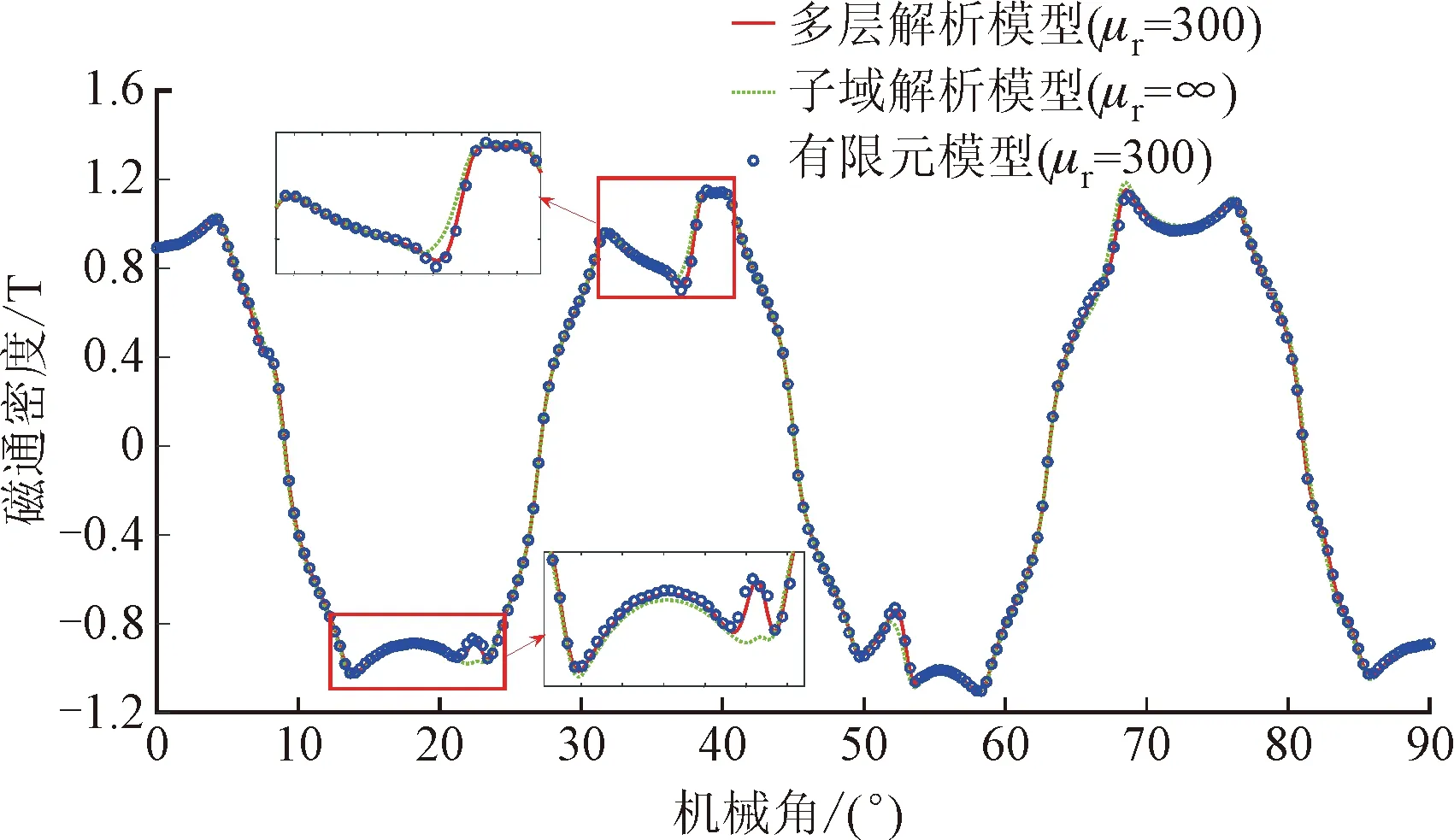
(a)径向分量

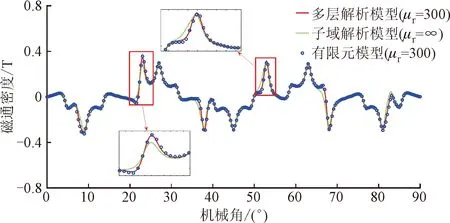
(b)切向分量

图10为负载工况下,电枢绕组层(区域Ⅳ)平均半径处的磁感应强度径向和切向分布曲线对比。可以看出多层解析模型的计算结果与有限元模型计算结果依旧具有很好的一致性。

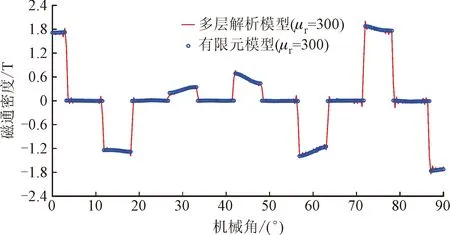
(a)径向分量

(b)切向分量

利用式(41)～(43)可以得到负载电流为70 A的工况下,电机在转速为2 000 r/min时的绕组磁链,如图11所示。可以看出,多层解析模型的计算结果与有限元模型的计算结果基本一致,而子域模型由于没有考虑定子铁心材料的磁阻,计算所得到的磁链结果偏大。

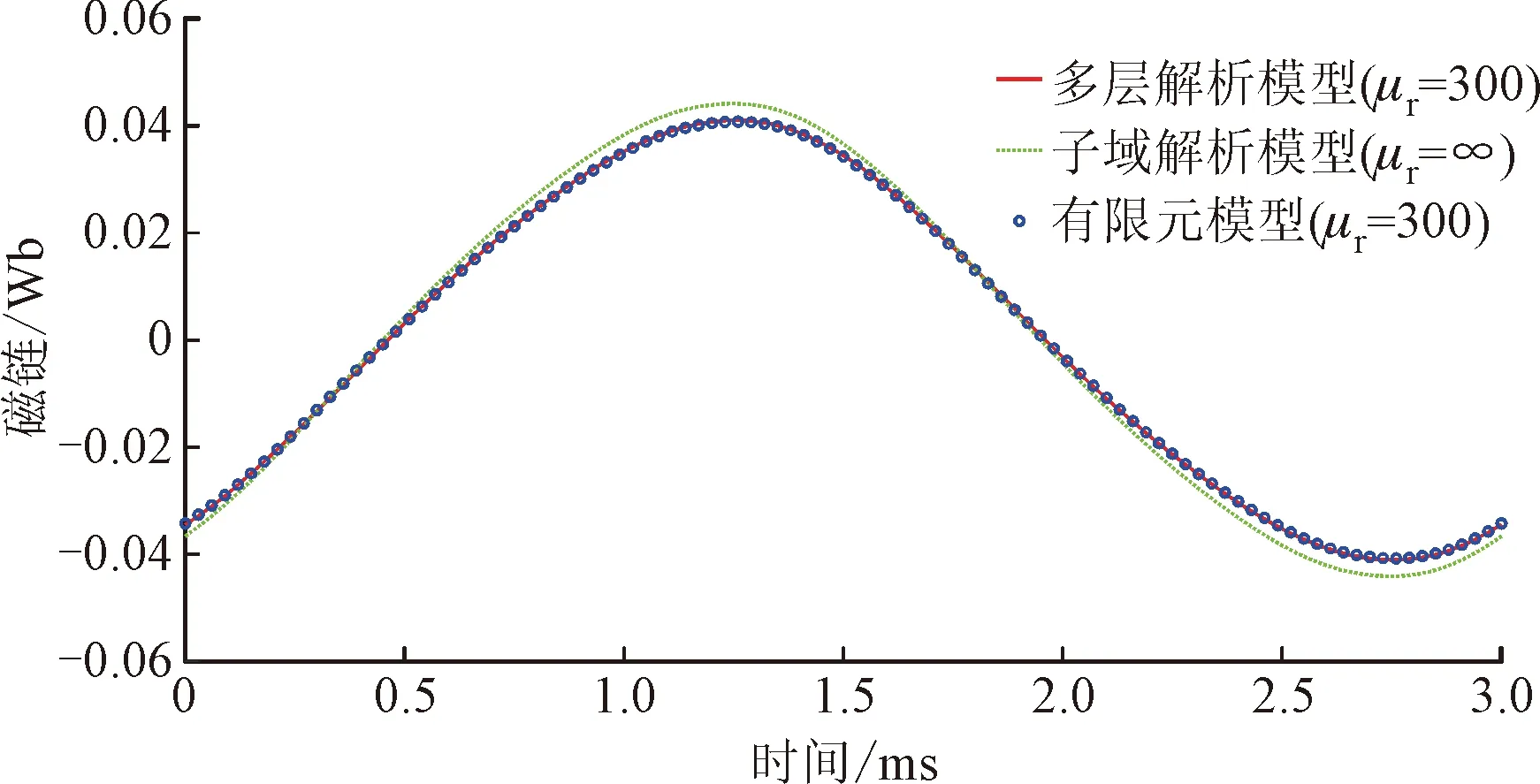
图11 转速为2 000 r/min时的负载磁链Fig.11 On-load flux linkage at 2 000 r/min

当负载电流I=70 A时,式(45)计算得到三段式Halbach阵列永磁电机的输出转矩。图12所示是多层解析模型、子域模型和有限元模型输出转矩计算结果的对比。图12中Tavg为平均转矩,Trip为转矩脉动,其计算公式为

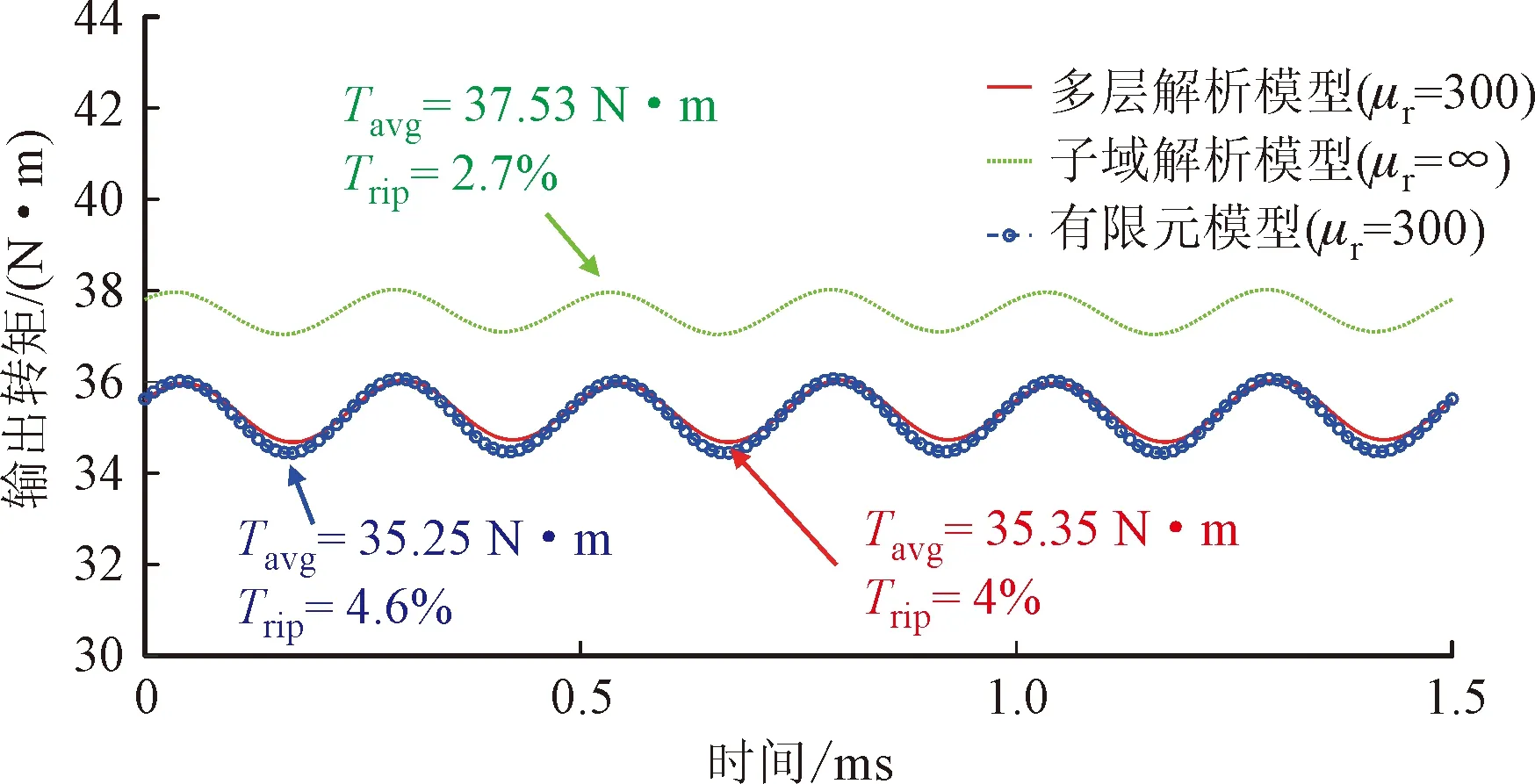
图12 两种解析模型与有限元模型输出转矩的计算结果对比Fig.12 Comparison of the results of output torque calculations for two analytical models and FEM

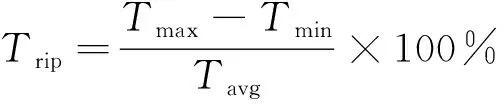
(46)

式中:Tmax和Tmin分别是转矩曲线上的最大和最小转矩值。

可以看出多层解析模型计算得到的输出转矩曲线与有限元模型的转矩曲线吻合很好,多层解析模型计算得到的输出转矩平均值为35.35 N·m,有限元计算得到的输出转矩平均值为35.25 N·m,两者相差0.1 N·m,相对误差小于1%。无法考虑铁心材料磁导率的子域模型计算得到的输出转矩平均值为37.53 N·m,计算结果偏大,且计算得到的转矩脉动偏小。

通过空载和负载的电磁性能计算结果的对比证明了本文提出的三段式Halbach阵列永磁电机多层解析模型的正确性。此外,多层解析模型计算拥有150个数据点的转矩曲线,需要的时间为2 390.14 s,计算拥有同样数据点个数的输出转矩曲线,有限元模型需要的时间是3 034 s。多层解析模型在具有较高计算精度的同时也具有计算速度快的优点。

5.3 槽开口宽度对输出转矩的影响

槽开口宽度影响气隙中的磁场分布,从而直接影响转矩性能,本节利用多层解析模型分析了改变槽开口宽度对输出转矩的影响。由图13可以看出,随着槽开口宽度的增大,电机的输出转矩平均值先增大后减小。转矩脉动随着槽开口宽度的增大而增大。在三段式Halbach阵列永磁电机的设计之初要综合考虑转矩输出能力和输出转矩脉动来选择合适的槽开口宽度。

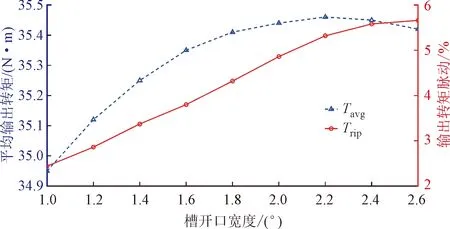
图13 槽开口宽度对输出转矩的影响Fig.13 Influence of slot opening width on torque

5.4 磁极宽度和充磁夹角对输出转矩的影响

对于三段式Halbach阵列永磁电机来说,磁极宽度θ2和充磁夹角θm都会影响气隙磁密,从而影响输出转矩。所以,选择合适的主磁极宽度和充磁夹角才能进一步提升电机的转矩性能。本节基于三段式Halbach阵列永磁电机的解析模型,分析了充磁夹角θm和主磁极与副磁极的宽度比ε对输出转矩的影响。ε可以表示为

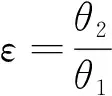
(47)

图14是磁极宽度比ε和充磁夹角θm变化对平均输出转矩的影响规律,可以看出当磁极宽度比ε不变时,增大充磁夹角,电机的输出转矩先增大后减小。当θm=0°时,所有磁极宽度比下的电机永磁体都为径向充磁结构,输出转矩不随磁极宽度比ε的变化而变化。当0°<θm<75°,增大宽度比ε,电机的平均输出转矩先增大后减小。当75°≤θm≤90°,增大宽度比ε,电机的平均输出转矩增大。最大转矩点为θm=45°,ε=3处,最大输出转矩平均值为35.43 N·m。

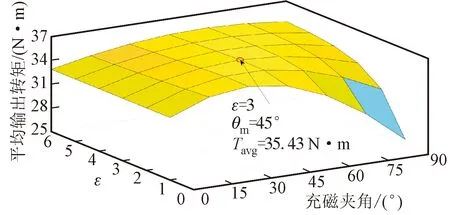
图14 磁极宽度比和充磁夹角对平均输出转矩的影响Fig.14 Influences of pole width ratio and magnetization angle on average output torque

图15是磁极宽度比ε和充磁夹角θm变化对输出转矩脉动的影响规律,可以看出,当磁极宽度比ε不变时,增大充磁夹角,电机的转矩脉动先减小后增大。当θm=0°时,所有拓扑结构下永磁体都为径向充磁结构,转矩脉动不随ε的变化而变化。当0°<θm≤90°时,增大ε,转矩脉动呈现先增大后减小再增大的趋势,最小转矩脉动点出现在θm=45°,ε=4处,最小的转矩脉动为0.93%。

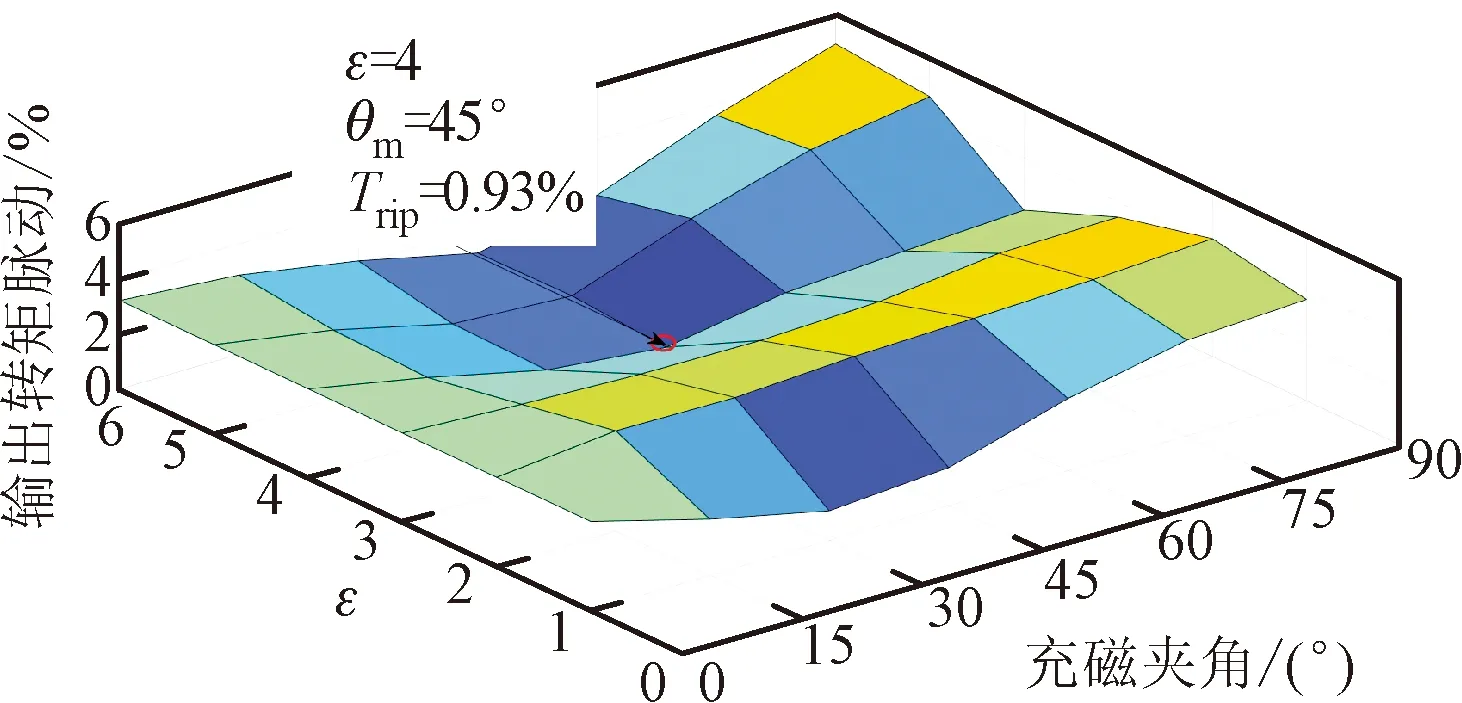
图15 磁极宽度比和充磁夹角对输出转矩脉动的影响Fig.15 Influences of pole width ratio and magnetization angle on torque ripple

5.5 转矩最优点验证

从5.3和5.4节的分析结果可以看出,当槽开口宽度为1.8°时输出转矩能提高,同时转矩脉动的变化不大。当磁极宽度比为4、充磁夹角为45°时,平均输出转矩能够有效提升,同时转矩脉动能实现大幅度的削减。根据影响规律的分析结果,将槽开口宽度1.8°、磁极宽度比4和充磁夹角45°作为电机输出转矩的最优设计方案。优化后的输出转矩曲线如图16所示,相较于初始的三段式Halbach阵列永磁电机结构,优化后的平均输出转矩提升了0.13 N·m,同时转矩脉动实现了大幅度的削减,优化后转矩脉动仅有0.97%,相比于初始结构,转矩脉动削减了75.7%。而且多层解析模型计算结果与有限元模型计算结果基本吻合,再一次证明了多层解析模型的正确性。

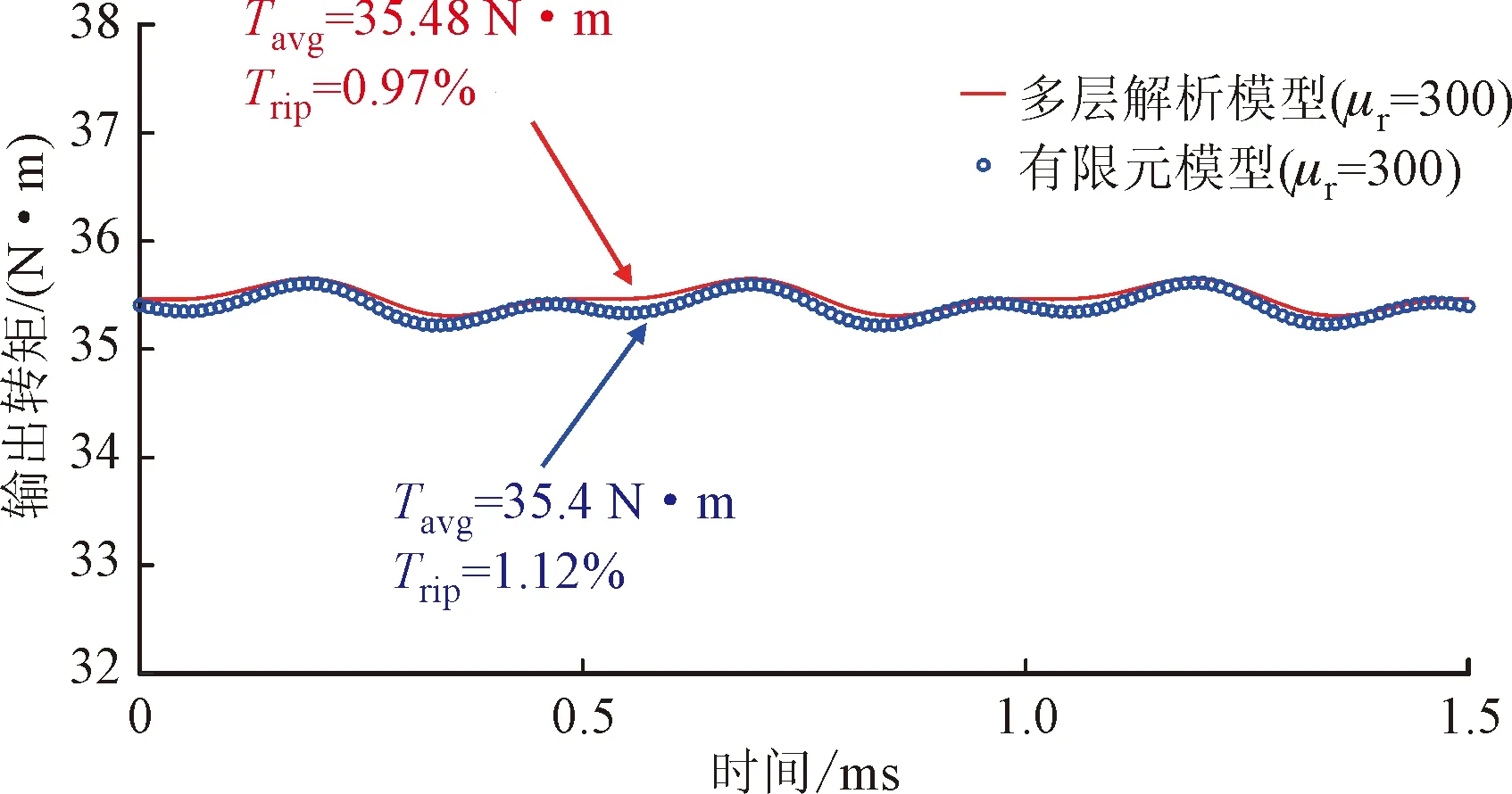
图16 优化后的输出转矩Fig.16 Optimized output torque

6 结 论

本文提出了一种考虑软磁材料磁导率为具体值的三段式Halbach阵列永磁电机的多层解析模型和建模方法。该方法根据激励源和媒介的不同对电机全域进行了划分,考虑了槽开口和实际槽深等复杂结构。利用该多层解析模型可以计算不同工况下电机内部磁场的分布,也可以计算磁链、反电动势和转矩等主要电磁性能,计算结果与有限元模型计算结果高度吻合,证明了多层解析模型的正确性。同时,研究发现传统子域模型计算得到的磁链、反电动势和输出转矩平均值相比于多层模型和有限元模型偏大,齿槽转矩和输出转矩脉动偏小,这是由于子域模型忽略软磁材料磁阻所导致的。

相比于有限元模型,本文所提出的多层解析模型可以快速调整三段式Halbach阵列永磁电机的结构和电磁参数。基于该特点,研究了槽开口宽度、磁极宽度和充磁夹角对输出转矩性能的影响规律,并给出了输出转矩最优的设计方案。更重要的是,本文提出的多层解析模型在磁场的求解速度上快于有限元模型,这对于电机的初始设计、电磁性能影响规律分析以及后期的参数优化都具有明显的优势。