材料与载荷随机性影响下管路结构振动疲劳可靠性分析方法

高玉闪,杨茂,李斌,杜大华,王珺,李斌潮,周建

(1. 西安航天动力研究所液体火箭发动机技术重点实验室,710100,西安;2. 航天推进技术研究院,710100,西安; 3. 西安交通大学航天航空学院,710049,西安)

2015年以来,蓝色起源公司及SpaceX 公司成功验证液体火箭发动机的回收使用,引发各航天强国对可重复使用技术的高度关注[1]。与传统一次使用发动机以性能为主不同,可重复使用发动机更关注核心部组件的可靠性寿命设计。在关键组件中,管路在振动载荷下的失效为液体火箭发动机主要故障模式之一[2-3],因此研究者就管路的振动疲劳寿命及抗振动疲劳设计进行了大量研究。Du等[3]通过小尺寸对接焊管道振动疲劳试验,研究了管道振动疲劳裂纹萌生及扩展特征,并通过寿命缩减系数[4]修正,获得火箭发动机焊接管路设计用高置信度、高可靠度S-N曲线。Du等[5]将加速度的功率谱密度作为随机载荷,基于有限元方法对火箭发动机管路进行了危险点位置的确定和不同的激励方向上均方根应力、疲劳寿命的计算,并与试验对比,验证了该方法的有效性。王帅等[6]建立预载荷及随机振动载荷下管路结构疲劳损伤分析方法,并分析了某运载器输送管路的确定性振动疲劳寿命。杜大华等[7]针对某型火箭发动机管路断裂失效的问题,提出了管路的动强度失效分析方法与动力优化设计方法,并评估了管路结构的确定性寿命。方红荣等[8]基于频域疲劳寿命计算方法,评估了某运载火箭发动机输送管路的确定性随机振动疲劳寿命。张亚琪等[9]建立了基于梁单元的管路随机振动分析模型,简化了管路确定性随机振动疲劳寿命的评估计算,并分析了管路减震卡箍对管路疲劳的影响。综合来看,现阶段对液体火箭发动机管路振动疲劳寿命的研究主要集中于管路确定性疲劳寿命评估及抗振动疲劳结构设计两方面,而鲜见管路的振动疲劳寿命可靠性的研究工作。

在压力容器、航空、车辆工程等行业,管路等部组件振动疲劳寿命及可靠性问题同样是研究人员的关注重点[10-18]。以载荷及寿命修正系数的方式考虑材料疲劳性能、结构尺寸、表面状态及载荷环境随机性的影响,ASME BPVC 标准[4]中给出各种金属材料的设计用疲劳曲线。基于对有限采样时间内实测车架载荷序列的处理和分析,张茜等[10]考虑时序载荷的随机性,将时域疲劳载荷谱施加于车架有限元模型,仿真获得危险点应力时间序列,并评估车架振动疲劳寿命。利用相似的处理方式,周凌波[11]对航空加筋板的振动疲劳寿命进行了时域样本法估算,并对比评价了5种频域方法,发现Dirlik方法[12]精度最好。针对海底管道在波流联合作用下的疲劳破坏问题,相关学者[13-14]参考应力-强度可靠性模型[15],以经验分布及变异系数的方式,考虑载荷、材料及应力计数程序中的随机性影响,提出管路跨涡激振动疲劳失效可靠性分析方法。针对静态疲劳,借助模型仿真,相关学者[16-18]考虑底层变量的随机分布,抽样获得底层变量对寿命可靠性的影响,并拟合结构疲劳可靠性功能函数响应面[19],在此基础上,利用蒙特卡洛方法[20]多次抽样,获得结构的疲劳寿命可靠性,但在振动疲劳领域鲜见类似研究。

本文考虑关键因素(振动载荷及材料)的随机性影响,建立结构振动疲劳寿命可靠性分析模型,与时域方法对比,证明本文随机性模型对不同类型载荷的适用性。以典型管路结构为研究对象,分析液体火箭发动机管路结构寿命分散及产生原因,评估示例结构寿命可靠性,并给出液体火箭发动机管路寿命缩减系数取值以指导工程应用。

1 管路振动疲劳可靠性评估

现阶段,针对火箭发动机管路振动疲劳寿命评估,如图1所示,已形成通用的分析流程[3-7]如下:

图1 火箭发动机管路振动疲劳寿命模型Fig.1 Vibration fatigue life model of rocket engine pipeline

(1)在试车或飞行试验测点响应数据的基础上,通过快速傅里叶变换获得管路结构一定频率(f)范围内输入载荷l的功率谱密度(PSD)L(f);

(2)建立结构动力学模型,并通过模态试验获得的结构振动特性信息对动力学模型进行修正或优化,提高其仿真精度;

(3)借助修正动力学模型,施加载荷PSD,求解获得危险点动应力PSDΣ(f),并考虑静应力对平均应力的修正,利用寿命评估方法获得管路寿命N。

考虑到材料疲劳性能、载荷及结构几何等因素随机性影响下,在确定性寿命N基础上,必须考虑一定的寿命缩减系数C[3-4],才能获得较高可靠度的寿命NP。在火箭发动机管路可靠性寿命评估中应用时,寿命缩减系数一般基于相关行业的经验取定[3],而其取值合理与否未见相关研究报道。此外,静态疲劳寿命可靠性研究[16-18, 21]表明,材料的疲劳性能分散为结构疲劳寿命分散的主要原因,而对于振动疲劳,载荷本身同样具有很大的随机性。因此,有必要从底层关键随机性因素——材料性能、载荷出发,建立管路结构振动疲劳可靠性寿命模型,为振动环境下管路结构高可靠度疲劳寿命评估及寿命缩减系数取值提供理论依据。

从完整的再现振动载荷随机性对结构的影响出发,时域方法需随机产生载荷序列,然后仿真加载获得危险点应力响应随机序列。准确模拟结构的振动过程及其随机性,往往需仿真巨量的载荷序列,工程应用时繁琐、效率较低[11]。在频域上,在多次实测采集数据的基础上,随机振动载荷可以用唯一的统计特征,如功率谱密度函数描述,进而获得危险点应力PSD统计信息,并进一步等效为经验的雨流计数[22]幅值概率分布,效率较高。但是,此类方法在应用时,不同时段载荷的随机性被多次平均抹除,难以描述实际的时序分散程度。此外,振动疲劳导致的结构破坏多属于高周甚至更高周次疲劳破坏范畴,而随着应力水平的减小,疲劳寿命的分散性有增加趋势[23]。因此,载荷水平对材料疲劳特性分散性的影响同样应在可靠性寿命模型中予以考虑。

综上,本文研究的问题主要为:振动环境下,考虑载荷、材料疲劳特性随机性,并计及工程应用要求的计算效率,对管路结构疲劳可靠性寿命进行评估。

2 振动疲劳可靠性模型

2.1 载荷水平影响材料疲劳特性随机性模型

在进行结构振动疲劳寿命分析时,主要借助疲劳试验,获得名义应力S与断裂寿命N之间的经验关系描述材料的疲劳性能,即S-N方程。为兼顾振动疲劳高周(线性段,N=105～107)及更高周次(平台段,N=107～109)寿命计算需求,本文采用三参数S-N方程描述材料的应力疲劳寿命规律,定义如下

N=C(S-Sf)-m

(1)

式中:C及m为材料常数;Sf为高周疲劳极限,可由成组试验[24]疲劳寿命数据拟合获得。

注意到三参数S-N方程中应力与寿命之间的对数线性关系,本文建立如下材料疲劳特性分散性模型

lgN=c-mlg(S-Sf)+δ(S)N(0, 12)

(2)

式中:c=lgC;N(0, 12)为标准正态分布;δ(S)为确定性应力水平S下的材料疲劳寿命分散系数。为描述寿命分散程度随应力水平变化规律,本文假设其与确定性应力水平之间同样满足对数线性关系,即

δ(S)=bS+kSlg(S-Sf)

(3)

式中:bS及kS为方程系数,可由各应力水平成组试验疲劳寿命方差拟合获得。

2.2 振动载荷随机性模型

在试车或飞行试验测点响应数据的基础上,通过快速傅里叶变换,获得管路结构一定频率范围内输入载荷的PSD函数。此时,载荷序列幅值随机性以确定性统计特征的形式被保留,而相位信息在多次平均后被消除。从满足工程应用的高效性出发,本文考虑在频域确定性模型基础上,由确定性载荷PSD获得结构应力确定的频域响应。在此基础上,引入相位的随机性,并通过傅里叶逆变换[10-11,24]获得随机的应力时域序列。在满足高效性的同时考虑载荷随性对结构应力的影响。

假设在施加的频域载荷激励下,结构危险点应力频域响应,即应力PSD为

(4)

式中:f为频率;fb及fu为动力学仿真频率上、下限。设定频域采样点数nf=2nh满足nh为整数,频率分辨率Δf满足nhΔf>fu,对应力PSD进行离散采样,获得对应的频谱Gσ(fk)。然后,进行对称扩展[24],获得双边谱Gσσ(fk)

(5)

则第k采样点,应力频谱模值为

(6)

综上可以看出,应力频谱模值由确定的载荷PSD函数而来,因此在寿命分析中是确定的。在此基础上,本文假设各采样点相位φk在[0, 2π)区间内随机取值,且满足一定分布,即

φk=F(k)

(7)

式中:F为特定分布函数。通常,对时域各态历经随机序列,F为均匀分布。

在模值及相位确定的基础上,对应力离散频谱进行傅里叶逆变换[10-11,23],即可获得TC=1/Δf时长内危险点应力随时间变化序列为

(8)

式中:tj为时域采样点,满足j=0, 1, …,nf-1。

2.3 振动疲劳可靠性寿命高效模型

对危险点应力时域序列进行循环计数处理,并叠加静应力产生的平均应力,即可获得危险点应力均值、幅值统计分布规律。假设统计后j循环时危险点应力均值为σm、幅值为σa,则根据Goodman关系[26],可得换算至应力比为-1时的有效应力σeff满足

(9)

式中:σb为材料极限强度。基于式(2)考虑材料疲劳特性随机性的影响,进一步获得j循环应力作用下结构危险点的随机寿命,即

(10)

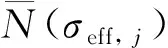
本文认为对同一危险点,材料的随机性表征应一致,即针对同一应力序列,rN取值应相同。由此,根据Miner线性累计理论,应力时域序列{σ}t下结构危险部位疲劳损伤为

(11)

式中:nσ, j为应力水平σeff, j在应力序列中出现的次数。基于式(11)可知,本文构造的振动疲劳损伤计入了静应力及平均应力的影响,还考虑了载荷对平对材料疲劳特性分散性的影响,更接近工程实际。

在应力序列对应的损伤基础上,结构疲劳寿命t定义为

(12)

式中:T为分析应力序列对应的时长,为尽可能真实反映载荷分散性的影响,一般应满足T≥t。

为充分评估结构振动寿命的可靠性,需对结构振动寿命的分布特征进行充分评估。因此,在危险点应力确定性PSD基础上,需多次抽样变换随机产生应力序列并计算结构寿命,导致循环计数计算量较大。特别是对高周或更高周疲劳问题,满足应力序列长度不小于结构寿命条件时,对应的应力序列过长,循环计数计算量工程不可接受。

实际上,对确定的PSD谱转换的应力序列,当序列长度超过一定有限值后,循环计数处理获得的有效应力序列将出现稳定的统计特征。即存在一有限值TC,满足

T→TC;Fσ, T→Fσ, TC

(13)

式中:Fσ为有效应力σeff特定的分布函数。由此,将应力时域序列循环计数,转换为特定分布的有效应力抽样,大幅缩减结构寿命分析计算量及时间成本。在此基础上,首先确定一系列TC时间长度内损伤

(14)

式中:nC为TC内有效应力样本数量。进而,结构振动疲劳寿命为

(15)

式中:n为满足nTC≥t的最小整数。

综上,本文振动疲劳寿命高效模型分析流程如图2所示。在此基础上,进行多次抽样,获得振动疲劳寿命分布,即可评价寿命可靠性。

图2 结构振动寿命高效仿真分析模型Fig.2 Efficient simulation model for vibration fatigue life analysis for structure

3 模型分析及讨论

3.1 典型材料疲劳性能随机性模型验证及分析

典型材料疲劳性能数据如图3所示,其中σ0及N0分别为参考应力及其对应的参考寿命。可见,材料疲劳性能在各应力水平下均存在明显的分散性,同时,不同应力水平下,疲劳寿命的分散性有明显差异。在1.27σ0、1.14σ0、1.02σ03个应力量级下,典型材料疲劳寿命分布如图4所示,对照参考曲线可知其存在明显的对数正态分布特征,由此,证明本文利用对数正态分布(式(2))描述材料寿命分散的合理性。同时可以看出,随着应力水平的增加,材料疲劳特性分散程度有增加趋势。对不同应力水平材料的寿命数据进行对数正态分布拟合,获得拟合均值及方差如图5所示,可见两者均随着应力的增加而增加,且规律几乎相同。因此,本文用相同规律(式(2)及式(3))描述了寿命均值及方差随应力变化规律。

图3 典型材料应力疲劳试验数据及拟合Fig.3 Stress fatigue test date of typical material and its fitting

图4 典型材料不同应力水平下疲劳寿命分布Fig.4 Fatigue life distribution under different stress levels of typical material

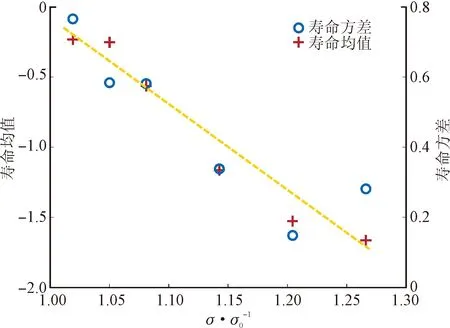
图5 应力水平对疲劳寿命均值及分散影响规律Fig.5 Effect of stress level on the mean and dispersion of fatigue life

对试验数据进行拟合,即可获得材料疲劳特性随机性模型参数,如表1所示。在此基础上,识别典型材料不同可靠度对应S-N方程如图3所示。

表1 典型材料疲劳特性随机性模型参数

3.2 载荷随机性模型验证及分析

假设线性系统的运动状态及应力状态方程描述如下

(16)

式中:M=0.001、μ=0.01、K=40π2及A=1为系统无量纲参数;F(t)为外加时域无量纲载荷;x为载荷作用点无量纲位移,满足零初始条件。

考虑F(t)为如下载荷谱对应时域序列

GF(f)=1,f∈[1, 1 000)

(17)

取t=0～20 s,对系统施加载荷F(t),利用时域积分,求解载荷作用点位移分布如图6(a)所示。利用频域方法,直接求解载荷作用点位移响应PSD,如下

(a)位移时间序列

(b)位移峰谷值

(18)

式中:H(f)为单自由度频响函数。通常,利用谱宽系数ε或不规则因子γ描述不同谱型的功率谱,定义为

(19)

式中:m0、m2及m4分别为功率谱的零阶、二阶及四阶谱距。由此,求解载荷作用点位移响应PSD的谱宽系数为0.217,为窄带过程。

基于响应PSD,并假设位移响应相位[0, 2π)区间均匀分布,参考2.2节,构造时域位移响应分布同样在图6(a)示出,可见两者取值范围相当。统计两种模型位移峰谷值分布如图6(b)所示,对比可知两者分布几乎重合。进一步,基于式(16)计算获得无量纲应力时域序列,并利用雨流计数对时域积分模型及本文模型获得的序列进一步处理,获得两类模型载荷幅值及均值分布对比如图7所示,同样发现两模型的分布特征重合。由此证明,本文模型可精确表征窄带载荷时域序列分散性对应力的影响。

(a)应力幅值

(b)应力均值

为进一步验证本文载荷随机性模型的适用性,考虑F(t)为定义如下的宽带载荷谱对应时域序列

(20)

同时,修改系统参数μ=0.5,基于式(18)求解载荷作用点位移响应PSD,并按照式(19)计算获得该PSD的谱宽系数为0.739,为宽带过程。按照时域方法及本文方法构造应力时域序列,并利用雨流计数统计两序列应力幅值及均值(无量纲值)分布对比如图8所示,可见两模型的分布特征重合。由此证明,本文模型同样适用于宽带载荷时域序列分散性对应力的影响仿真。

(a)应力幅值

(b)应力均值

3.3 振动疲劳可靠性寿命高效模型分析及讨论

对3.2节中线性系统窄带响应,参考2.2节,构造其20、200、400及500 s时间内时域序列,进行雨流计数获得幅值及均值分布。参考某典型材料取系统参考应力σ0=500、应力极限为σb=2.64σ0。在此基础上,根据式(9)获得不同时长对应系统有效应力(无量纲值)累积分布如图9(a)所示。可见,对3.2节线性系统,基于500 s时域序列获得的有效应力分布收敛。基于此,识别其有效应力分布密度函数如图9(b)所示。进一步,与3.1节建立的典型材料疲劳性能随机性模型联立,借助2.3节振动疲劳可靠性寿命高效模型,对系统振动疲劳寿命进行100次抽样,获得其寿命分布如图10所示。在此基础上,评估系统可靠性寿命如表2所示。

表2 系统振动疲劳可靠性寿命统计

(a)有效应力累积分布密度

(b)有效应力分布密度函数

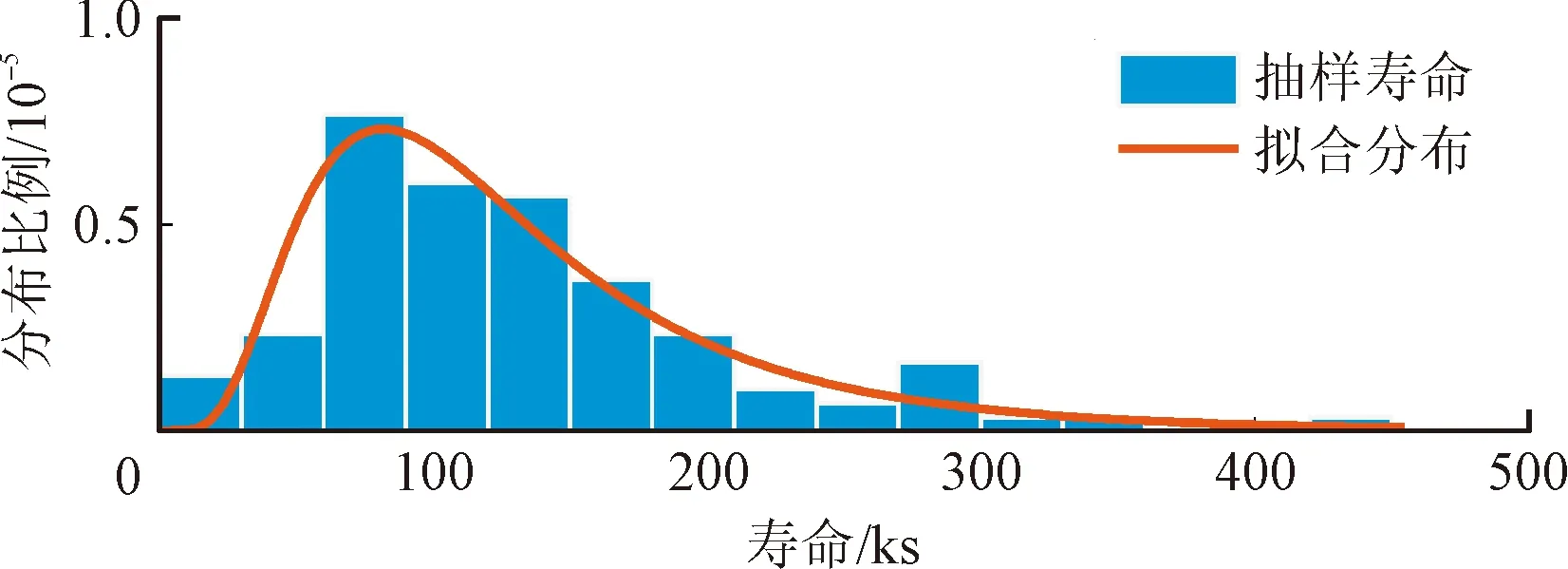
图10 系统振动疲劳寿命分布抽样及拟合 Fig.10 Sampling and fitting of the vibration fatigue life distribution of the system

对各次抽样计算时长及计算寿命累加可知,本文模型100次抽样总耗时为364.5 s,对应的时域序列总时长为1.3×107s。针对有限时长(本文取100 s)时域载荷序列,直接利用时域方法进行分析计算,多次试算获得其平均分析时长为251.6 s。由此,若直接使用时域方法抽样,估算相对总计算时间如表2所示,可见本文方法的计算效率提升效果显著。

4 管路结构可靠性分析及讨论

以某泵后摆液体火箭发动机煤油一级泵出口管为分析对象,如图11所示。其进口端与燃料一级泵相连,出口端与推力室相连,中间通过两个固定支板分别与燃料预压泵和燃气摇摆装置下法兰连接。在多次试车过程中,测点加速度监测数据显示该管路系统在336 Hz附近振动量级集中且偏大,可能存在动强度裕度不足问题,有结构疲劳破坏的潜在风险,从而影响到发动机的工作可靠性与安全性。

4.1 管路振动应力仿真分析及讨论

基于干模态试验结果修正有限元模型及其边界。注意到试车载荷振动能量集中在336 Hz附近,选取仿真所得4阶模态(第1阶、第2阶及336 Hz临近两阶336 Hz-1阶、336 Hz-2阶)振型及频率与模态试验[27]之间误差最小为优化目标,计算模型边界弹簧刚度为设计变量,进行响应面优化。优化后,管路部分第1阶及336 Hz-2阶对应模态振型与试验对比如图12所示,各优化阶次与试验频率对比如表3所示。由对比可知,4阶模态误差均在可接受范围内,认为修正后有限元模型在精度工程可接受的情况下可以反映目标管路结构的动态特性。

表3 管路干模态仿真与试验对比

(a)仿真1阶

(b)试验1阶

(c)仿真336 Hz-2阶

(d)试验336 Hz-2阶

实际试车测量显示,目标管路在工作过程中,内壁承受约0.065 8σ0的内压。考虑内压作用,仿真获得目标管路湿模态。进一步仿真获得目标管路振动过程中动应力分布如图13所示,最大动应力出现在管壁与法兰连接部位及弯管部位。

图13 振动时管路动应力分布Fig.13 Dynamic stress distribution of the pipeline under vibration

提取管路振动疲劳第1个危险点(见图13)应力PSD谱,构造一定时长的时域序列,通过雨流计数获得幅值及均值分布,进一步考虑平均应力修正获得有效应力分布。随着构造时长的增加,有效应力分布密度曲线趋于稳定,当构造时长为100 s时,分布稳定,稳定有效应力分布如图14所示,此时生成的密度包含真实载荷的所有随机性特征。其他危险点按照其1σ应力与主危险点之间比例关系可直接缩放获得。

4.2 管路振动寿命可靠性仿真分析及讨论

在有效应力随机分布已知的情况下,考虑局部材料疲劳特性随机性的影响,抽样100次获得各危险点失效概率累计分布如图15所示。由抽样结果可知:①各危险点抽样寿命基本符合对数正态分布(与图中对数正态分布参考线重合);②各危险点寿命均有明显的分散性,且随着应力降低,分散性变大。对抽样寿命进行分布拟合,获得危险点振动疲劳寿命对数正态分布均值及标准差,生成各危险点寿命分布如图16所示。在此基础上,提取不同可靠度寿命如表4所示,可见中值寿命与-3σ寿命存在较大差异。基于本文仿真计算结果,对目标管路,在中值寿命确定的基础上,至少应除以5以获得高可靠性寿命。综合考虑3危险点随机性,获得管路振动疲劳寿命分布如图16所示,可见综合寿命分布几乎完全由危险点1确定,但由于受到危险点2、3分散性影响,寿命分布有略微集中趋势。

表4 管路振动疲劳可靠性寿命统计

图15 管路危险点振动疲劳寿命抽样Fig.15 Vibration fatigue life sampling of dangerous point on the pipeline

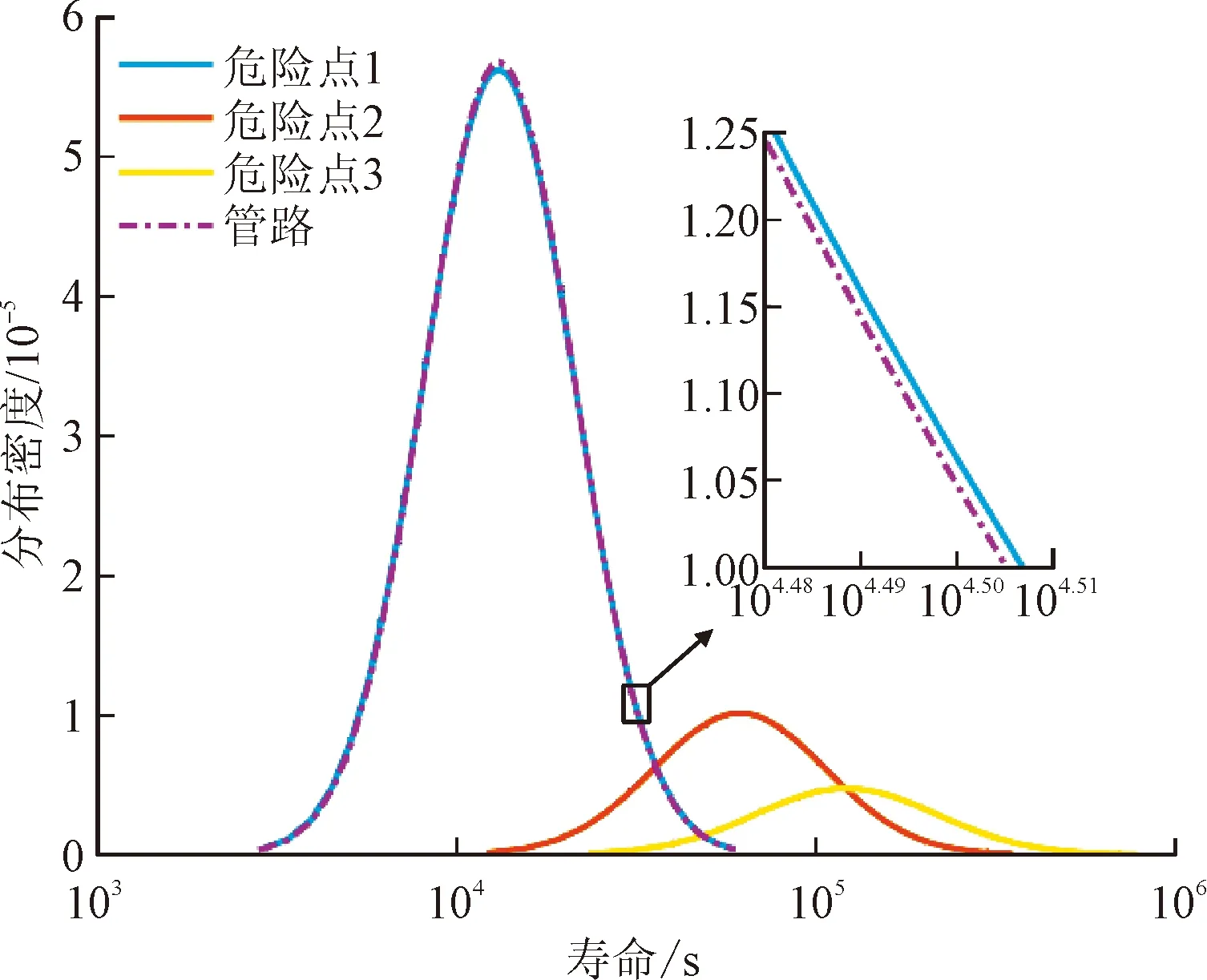
图16 管路综合振动疲劳寿命分布Fig.16 Comprehensive vibration fatigue life distribution of the pipeline

由图12、图13及表4分析结果可知,管路振动疲劳寿命存在较大的分散性。按平均材料性能评估管路的振动疲劳寿命,仅考虑载荷分散性的影响时,管路疲劳寿命分布如图17所示,可见寿命分布相对于综合考虑材料及载荷随机性时集中,均值略微上升。基于此分析结果可知,管路疲劳寿命分散性中,载荷和材料的影响比例约为23∶77,材料分散性占主导地位,但载荷分散随机性同样不可忽视。

图17 不同因素随机性影响下管路综合振动疲劳寿命分布Fig.17 Comprehensive vibration fatigue life distribution of the pipeline under influences of randomness of different factors

5 结 论

本文将载荷、材料疲劳特性随机性及载荷水平对材料疲劳特性随机性的影响引入结构振动疲劳寿命评估,考虑计算效率,建立振动疲劳可靠性寿命高效评价模型,并以典型材料试验结果及单自由度时域模型,证明了随机性模型的适用性及寿命模型的高效性。

对某泵后摆液体火箭发动机煤油一级泵出口管振动疲劳寿命可靠性进行评价,并分析其寿命分散程度及底层因素随机性对其分散性的影响。分析结果表明:

(1)目标管路各危险点振动疲劳寿命符合对数正态分布,同时振动疲劳寿命存在明显的分散性,且随着危险点应力降低,分散性变大;

(2)对管路结构,在确定性寿命的基础上,应考虑至少不小于5倍的寿命缩减系数,以覆盖载荷及材料的随机性影响,从而获得其高可靠度振动疲劳寿命;

(3)不同底层因素的随机性对管路振动疲劳寿命分散性的贡献不同,其中材料疲劳特性分散性影响显著,影响占比约为77%。