存在证据冲突的临近空间飞行器遥测数据相关性评价与融合方法

张少杰,荣海军,杨朝旭,侯凯振

(1. 西安交通大学机械结构强度与振动国家重点实验室,710049,西安;2. 西安交通大学陕西省先进飞行器服役环境与控制重点实验室,710049,西安;3. 西安交通大学航天航空学院,710049,西安)

临近空间的物质构成、能量输运以及相互作用极其复杂,对飞行器的长期驻空飞行带来了挑战。利用遥测数据实时监测飞行器飞行状态,是确保高可靠长航时稳定飞行的有效手段[1]。飞行器的能源、姿控、载荷等分系统之间接口交互,决定了遥测数据之间存在相关性。全参数的数据分析不仅导致信息冗余,增加了飞行器状态监测的工作量,而且难以检测出遥测数据之间相关关系的多元异常,使异常检测存在盲目性[2]。遥测数据之间关联复杂,任何一种飞行参数可能与多种参数之间存在相关关系,并且相关关系随时间而变化。人工通过物理知识获取相关性模型耗时且费力,并且一旦飞行器结构和环境发生变化,通常要重新分析相关性。借助相关性分析算法能实时分析遥测数据相关性,获取数据的潜在关系,便于监测飞行器状态[3]。欧洲太空局正是利用遥测数据之间的统计相关性进行异常检测,挖掘出与异常事件相关的遥测参数[4]。因此,分析飞行器遥测数据的相关性有助于监测飞行器在轨运行状态,保障飞行器正常运行。

围绕遥测数据相关性,国内外学者提出了多种分析方法,包括Pearson相关系数[5]、互信息[6]、最大信息系数(MIC)[7]和距离相关系数[8]等方法。Zhe等[9]利用Pearson相关系数,分析了飞行器遥测数据相关性,能够快速检测出与舱门泄漏率相关的参数。Pearson系数计算复杂度低,对随机噪声的鲁棒性强,但Pearson系数由于正态分布假设导致计算结果易受异常数据的影响。互信息不要求变量分布,但是难以计算概率密度函数,在互信息基础上学者提出了MIC方法[10]。崔树银等利用MIC对多元负荷数据进行相关性分析,筛选出相关变量。MIC能刻画数据间非线性关系,但是受网格划分数和方式的影响,计算时间复杂度高[11]。孙宇豪等采用距离相关系数对遥测数据进行自变量选择,提高了模型的预测性能[12]。距离相关系数通过特征函数距离衡量变量之间的相关关系,相比MIC时间复杂度低,但计算结果易受噪声数据的影响。此外,上述方法在遥测数据相关性分析的实践中存在结果冲突的问题。

由于现有的单一相关性方法存在一定的局限性,如果将不同优势的相关性分析方法融合,则能够提高分析结果的可靠性,因此考虑将优势互补的相关性分析方法融合。D-S证据理论具有坚实的理论基础,能在先验概率和条件概率都未知的情况下处理信息,提高判决结论的正确度和可信度[13]。考虑到D-S证据理论具有上述优势,本文采用D-S证据理论进行融合。但是当存在高度冲突证据时,D-S证据理论融合结果往往与常理相悖。Zhao等将证据冲突部分作为未知信息概率以处理证据冲突,但该方法会导致未知信息概率增加,无法获得有效融合结果[14]。孙全等使用证据的可信度处理证据之间的冲突部分,但由于可信度直接定义,导致结果存在主观性[15]。Shang等计算出n个证据的平均值,并使用D-S证据理论组合规则融合平均值[16]。该方法能够处理冲突,然而未考虑到证据之间的权重。利用证据权重修正证据源,能够降低冲突证据的影响。赵静等利用Jousselme距离计算证据权重,并对证据加权平均后再采用D-S证据理论组合规则融合[17]。该方法通过Jousselme距离考虑了证据间的关联性,利用焦元的交集与并集比值反映证据之间的相似性,但是证据焦元彼此独立,焦元的比值并不能充分利用各证据之间的信息。Lin等采用相容系数计算证据之间的权重并修正证据,考虑了证据之间的相互支持度,但是无法有效处理高度冲突证据下的一票否决和合成规则失效问题[18]。

为了解决临近空间飞行器的状态监测与相关性分析问题,考虑到现有单一的相关性分析方法的局限性,以及相关性分析实践中的证据冲突问题,本文在相关系数分析评价与优势组合的基础上提出了基于支持因子的证据理论融合算法。首先,选取优势互补的Pearson相关系数、Spearman 相关系数与距离相关系数,分析遥测数据的相关性,并根据分析结果,构建相关性证据的初始基本概率赋值函数。其次,利用支持因子计算出各证据之间的权重并对证据进行修正,使修正后的证据具有相同的重要程度,计算证据命题的分布权重,分配修正证据的冲突基本概率赋值函数,从而获得融合结果。最后,开展临近空间飞行器遥测数据相关性分析实验,结果表明所提方法提高了遥测数据相关性分析的可信度。

1 遥测数据相关性分析

存在证据冲突的遥测数据相关性分析方法包括相关性评价和证据融合两部分内容,如图1所示。考虑到现有单一的相关性分析方法的局限性,选取能够优势互补的Pearson相关系数、Spearman相关系数与距离相关系数,对临近空间飞行器遥测数据进行相关性计算,根据计算结果构造各相关性证据的初始基本概率赋值函数。考虑到相关性分析实践中存在冲突问题,在相关系数分析评价与优势组合的基础上,提出了基于支持因子的证据理论融合算法。利用支持因子计算出各初始证据之间的支持度,获得证据的权值并对初始证据进行修正,使修正后的证据具有相同的重要程度;根据证据支持度计算证据可信度,并获得证据命题的分布权重;最后分配修正证据的冲突基本概率赋值函数,获得相关性证据融合结果。

图1 遥测数据相关性分析方法框图Fig.1 Correlation analysis method for telemetry data

2 相关性评价

本节考虑到临近空间飞行器遥测数据之间关联复杂、数据量大、伴有随机噪声和扰动等特征,因此从随机噪声鲁棒性、异常数据抗干扰和数据非单调性角度,分别选取了Pearson相关系数、Spearman相关系数与距离相关系数进行分析对比。

2.1 相关系数选取

2.1.1 Pearson相关系数

Pearson相关系数ρx, y用于衡量数据间线性相关程度[19],表示为

(1)

2.1.2 Spearman相关系数

Spearman相关系数rs本质在于根据原始数据的排序位置进行相关性分析[20]。对两个集合(X,Y)进行升序或降序排序,并获得排行集合X′、Y′,元素xi、yi分别为Xi在X中的秩以及Yi在Y中的秩。将个数为n的集合X′、Y′中的元素xi、yi(1≤i≤n)对应相减,获得一个排行差分值di(=xi-yi),rs表示为

(2)

rs采用单调变换描述集合之间的相关性,不会因个别异常数据影响整体排序,故抗干扰能力强。

2.1.3 距离相关系数

距离相关系数通过X与Y间联合特征函数与各自边际特征函数的差量化相关程度[21]。距离相关系数R(X,Y)表示为

(3)

(4)

(5)

(6)

(7)

(8)

2.2 相关性评价实验

本节开展临近空间飞行器的遥测数据相关性评价实验。受传输环境影响,遥测数据下发时不可避免出现噪声,以连续分布的高斯噪声和不同时刻下的脉冲噪声为例分析噪声鲁棒性。同时,遥测数据之间关联复杂,本节也从非单调性角度进行评价。

2.2.1 高斯噪声鲁棒性评价

数据噪声模型可表示为

y(i)=x(i)+αn(i)

(9)

式中:x(i)是不加任何噪声的遥测数据;y(i)是加入噪声后的混合数据;α为噪声强度系数,α∈[0, 1],通过调节α去控制信噪比。随着α增大,信噪比减小,数据的噪声程度也随之增大。图2表示不含高斯噪声的原始遥测数据和含高斯噪声的遥测数据(信噪比为40 dB)。

图2 含或不含高斯噪声的遥测数据示意图Fig.2 Telemetry data with Gaussian noise

随着信噪比降低,数据之间的关联性减小,意味着相关系数的值随着噪声程度的增加而下降。因此,增加噪声程度,并比较相关系数的下降程度,若下降程度最小,则说明噪声鲁棒性最强。图3反映了不同高斯噪声下的相关系数,可见随着噪声程度的增加,相关系数在逐渐下降,但是下降程度却不同。图3中Pearson相关系数下降程度最低,表明其高斯噪声鲁棒性最强。因为Pearson相关系数适合描述随机分布的数据相关性,虽然加入了高斯噪声,但是数据整体依然服从随机分布,所以Pearson相关系数相比其他两种方法受高斯噪声影响更小。

图3 不同高斯噪声下的相关系数Fig.3 Correlation coefficients under different Gaussian noises

本节通过下降率衡量各相关系数的高斯噪声鲁棒性,下降率为不加噪声相关系数和加入噪声后相关系数之间的差值与不加噪声的相关系数的比值,计算结果如表1所示。Pearson、Spearman以及距离相关系数在不同高斯噪声下的下降率之和分别为0.59,0.939 1和1.050 0。因为下降率越小,噪声鲁棒性越强。因此,上述3种相关系数的高斯噪声鲁棒性排序为Pearson相关系数最高,Spearman相关系数次之,距离相关系数最低。

表1 不同高斯噪声下的相关系数下降率

2.2.2 异常数据抗干扰评价

脉冲噪声的鲁棒性体现了对异常数据的抗干扰能力。图4是加入不同时刻脉冲噪声下的经度遥测数据。图5反映了不同脉冲噪声下的相关系数,图中Spearman相关系数下降程度最低,表明其抗干扰能力最强。因为Spearman相关系数通过数据的秩进行相关性分析,个别扰动数据并不会改变整体数据的秩,所以Spearman相关系数相比其他系数抗干扰能力更强。

图4 含脉冲噪声的遥测数据示意图Fig.4 Telemetry data with impulse noise

图5 不同脉冲噪声下的相关系数Fig.5 Correlation coefficients under different impulse noises

本节依然通过下降率对比各相关系数的异常数据抗干扰能力,计算结果如表2所示。Pearson、Spearman以及距离相关系数在不同脉冲噪声下的下降率之和分别为0.488、0.042 5和0.220 6。因此,上述3种相关系数的异常数据抗干扰能力排序为Spearman相关系数最高,距离相关系数次之,Pearson相关系数最低。

表2 不同脉冲噪声下的相关系数下降率

2.2.3 复合噪声鲁棒性评价

向原始遥测数据中加入含脉冲噪声和高斯噪声的复合噪声,比较各相关系数的复合噪声鲁棒性。图6为不同信噪比下的含复合噪声的遥测数据。图7反映了不同复合噪声下的相关系数,图中Spearman相关系数下降程度最低,表明其对复合噪声的鲁棒性最强。Pearson相关系数受到其中脉冲噪声影响,在三者中的鲁棒性最差,距离相关系数位居中间。

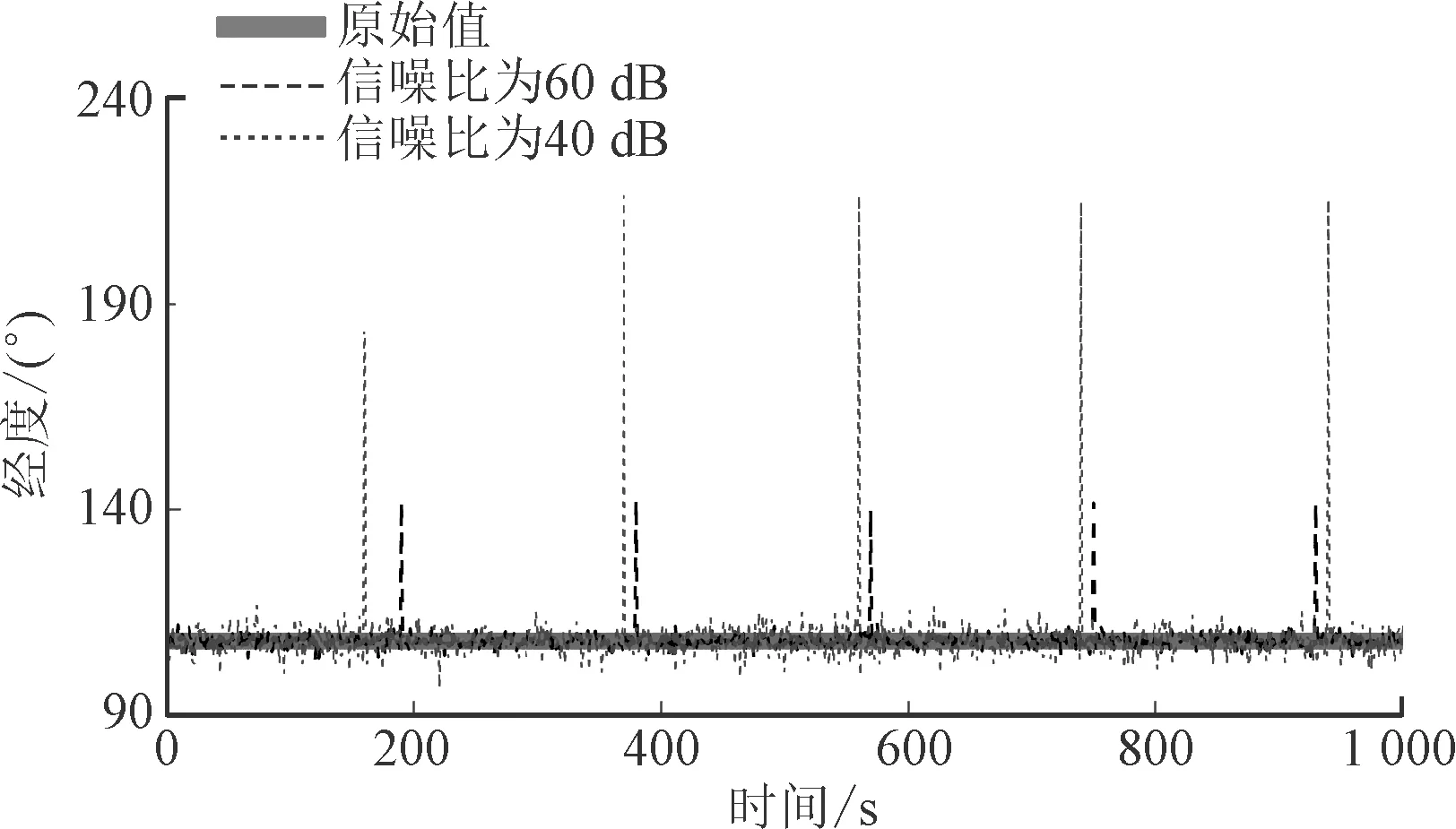
图6 含复合噪声的遥测数据示意图Fig.6 Telemetry data with composite noises

图7 不同复合噪声下的相关系数Fig.7 Correlation coefficients under different composite noises

表3反映了相关系数对复合噪声的鲁棒性。Pearson、Spearman以及距离相关系数在不同复合噪声下的下降率之和分别为2.141 8、1.544 8和1.755。因此,上述3种相关系数的复合噪声鲁棒性排序为Spearman相关系数最高,距离相关系数次之,Pearson相关系数最低。

表3 不同复合噪声下的相关系数下降率

2.2.4 非单调性评价

遥测数据之间关联复杂,多种复杂关系并存。数据之间也存在非单调关系。本节通过距离相关系数,与Spearman相关系数描述遥测数据之间的非单调关系。图8反映了平台北速(飞行器平台沿正北方向的运动速度)与平台俯仰角之间的非单调关系。分别用距离相关系数和Spearman相关系数计算两者相关性,距离相关系数的计算结果是0.975 3,Spearman相关系数的计算结果是0.180 4。由于Spearman相关系数需要通过数据的单调变化获得数据的秩,所以当数据非单调变化时,会影响Spearman相关系数的分析结果,而距离相关系数不需要对数据进行单调变化,因此距离相关系数相比Spearman相关系数更能够准确描述数据之间的非单调关系。

a)平台北速

(b)平台俯仰角

评价分析结果表明:Pearson相关系数计算复杂度低,对随机噪声的鲁棒性强,但异常数据抗干扰能力差;Spearman相关系数对异常数据抗干扰能力强,但不能准确识别数据之间的非单调关系;距离相关系数能够更准确地描述数据之间非单调关系,但是对随机分布的高斯噪声鲁棒性差。因此,Pearson相关系数、Spearman相关系数与距离相关系数相互互补,三者融合结果能够更全面体现遥测数据相关性。

2.3 存在证据冲突的相关性分析

Pearson相关系数、Spearman相关系数与距离相关系数相互互补,本节分别采用上述3种相关系数作为相关性证据对遥测数据进行相关性分析。表4是Pearson、Spearman和距离相关系数的遥测参数相关性分析结果。分析表4可知,3种相关系数在分析悬浮高度与大气压、悬浮高度与表面温度时,分析结果都趋于1,表明悬浮高度与大气压以及表面温度相关。在飞行器运动速度与氦气囊内的氦气温度相关性分析结果中,Pearson、Spearman相关系数结果表明二者不相关,距离相关系数的分析结果与Pearson、Spearman相关系数分析结果差异不大,但认为二者存在一定相关性。在空气温度与氦气体积的相关性分析结果中,Pearson相关系数结果表明二者不相关,而Spearman和距离相关系数结果表明二者强相关,此时3种相关系数的分析结果不一致,产生了冲突。上述方法在遥测数据相关性分析实践中存在结果冲突的问题,需要融合算法有效抑制证据冲突对分析结果的影响。

表4 遥测数据相关性结果

3 证据理论融合算法

在相关系数分析评价与优势组合的基础上,提出了基于支持因子的证据理论融合算法。首先,由于Pearson、Spearman和距离相关性证据的分析角度不同,各相关性证据重要程度不一定相同。所以,采用支持因子计算出各证据之间的权重并对证据进行修正,使修正后的证据重要程度相同。其次,为了解决D-S证据理论存在的一票否决和合成规则失效问题,通过计算证据命题的分布权重,分配修正证据冲突基本概率赋值函数,从而获得融合结果。

辨识框架Θ={A1,A2},命题A1表示相关,A2表示不相关。对于任意两个证据mi与mj(1≤i,j≤3)之间支持因子Sij为

(10)

式中:At⊆Θ,t=1或2,代表上述相关性证据的结果,即相关和不相关。支持因子既能够表征证据之间的支持程度和一致性,也从侧面反映了证据之间的冲突程度。式(10)所计算的支持因子保留了各证据之间的初始信息,同时综合考虑到证据的所有命题At,能直接体现出证据整体之间的相互支持程度。Sij取值范围为[0, 1],Sij若接近0,表明证据之间支持程度低,冲突性强;Sij若接近1,表明证据之间支持程度高,冲突性弱。

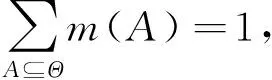
步骤1通过式(10)计算证据支持因子Sij,并依据Sij计算证据的支持度p(mi)。在计算出相关性证据mi与mj之间的支持因子Sij后,构造出一个3×3的支持因子矩阵S如下

(11)

m′i(A)=wimi(A),A≠Θ

(12)

m′i(Θ)=mi(Θ)+1-wi

(13)

式(12)、(13)获得了修正后的基本概率赋值函数m′i(1≤i≤3)。式(12)使证据权重小的相关性证据对命题A所提供的确定性信息减小;式(13)使证据权重小的相关性证据所提供的不确定性信息增加。因此,减小了证据权重小的证据对整个融合系统的影响。经过式(12)、(13)修正后,各相关性证据的重要程度相同。

步骤3计算证据的命题分布权重并改进组合规则。通过命题分布权重分配修正证据的冲突基本概率赋值函数,获得融合结果[25],表示为

(14)

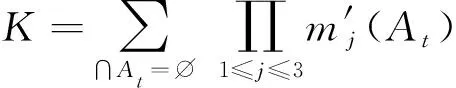
4 遥测数据分析结果

本节基于表4的相关性结果,构造相关性证据并开展证据融合,从证据冲突大和证据冲突小两种情况分别进行相关性分析。

4.1 证据冲突小情况下的相关性分析结果

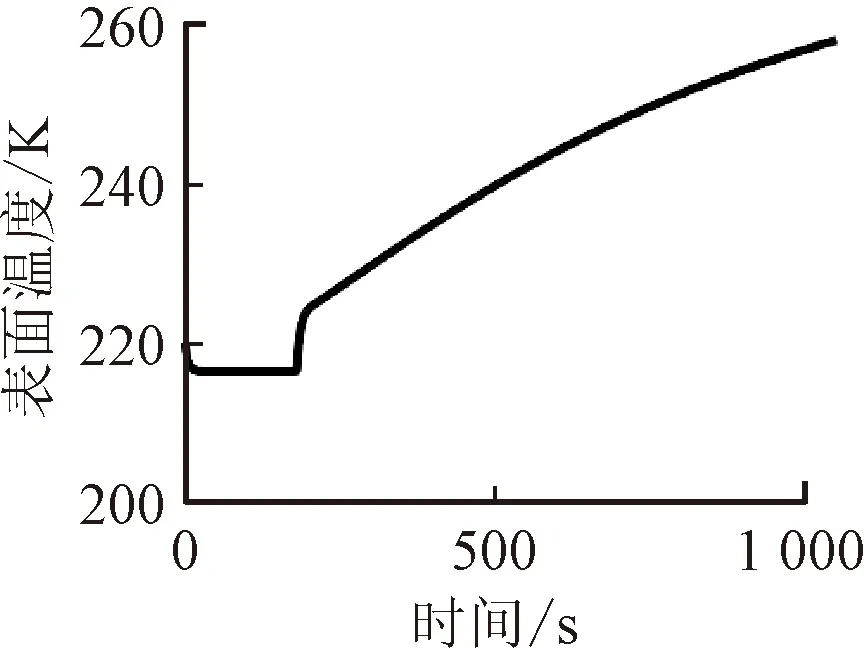
飞行器悬浮高度与其表面温度的相关性证据及融合结果如表5所示。上述基本概率赋值函数相关概率都接近1,表明悬浮高度与表面温度相关,证据分析结果一致。图9是悬浮高度与表面温度的变化过程曲线,表面温度随悬浮高度的增加而增加。图9与表5都充分体现出二者的相关性。飞行器在上升过程中表面温度升高,两者整体上呈现强相关关系,但上升阶段初期悬浮高度出现振荡,导致不是严格线性相关关系。

(a)悬浮高度

(b)表面温度

飞行器运动速度与氦气温度的相关性证据如表6所示。Pearson、Spearman相关性证据结果表明速度与氦气温度不相关,但是距离相关性证据结果表明二者存在一定相关性。此时存在证据冲突,采用式(10)计算支持因子,可得S12=0.998 9,S13=0.859 9,S23=0.834 4,由此可得支持度分别为1.858 8、1.833 4和1.694 3。分析表4中速度与氦气温度的Pearson与Spearman相关系数,可得出两者支持度接近。选择支持度最高的证据进行修正,m1的支持度最高,故为关键证据。

表5 飞行器悬浮高度与表面温度相关性证据及融合结果

表6 飞行器运动速度与氦气温度的相关性证据

表7 修正的飞行器运动速度与氦气温度相关性证据及融合结果

4.2 证据冲突大情况下的相关性分析结果

表9 修正的空气温度与氦气体积的相关性证据及融合结果

表8 空气温度与氦气体积相关性证据

(a)空气温度

为验证本文所提方法的有效性,与其他文献方法进行对比,结果如表10所示。经典D-S证据理论融合结果极易受到冲突证据的影响;文献[14]方法在处理冲突时,将冲突部分全部赋给未知信息,导致未知信息过大,分析结果造成偏差;文献[16]方法对平均证据进行D-S证据理论组合,但忽略了证据之间的支持度,结果并不理想;文献[18]方法采用相容系数计算证据权重,考虑了证据之间的相互支持度,融合结果相对较好。本文方法的相关概率计算结果相比文献[18]计算结果提高了约6.55%,比文献[16]计算结果提高了约26.84%,故本文利用基于支持因子的证据理论融合算法使相关性分析结果的可信度进一步提高,有效解决了相关性分析中的证据冲突。

表10 空气温度与氦气体积的相关性证据融合结果对比

5 结 论

临近空间飞行器长时间滞空飞行,状态发生异常甚至系统故障的频率大大增加。遥测数据相关性分析结果有助于监测飞行器的状态及检测故障。

(1)针对实际工程中遥测数据关联复杂、数据量大,实时下发伴有噪声等特点,考虑现有的单一相关性分析方法无法同时解决上述问题,采用融合优势互补的相关性分析方法,以提高分析结果的可靠性。评价实验证明,Pearson相关系数、Spearman相关系数与距离相关系数性能互补,3种相关系数融合有助于更全面地分析遥测数据的内在关联。

(2)由于Pearson相关系数、Spearman相关系数与距离相关系数在遥测数据相关性分析的实践中存在结果冲突的问题,因此在相关系数分析评价与优势组合的基础上,提出了基于支持因子的证据理论融合算法,通过支持因子计算权重及修正相关性证据,并分配修正证据的冲突基本概率赋值函数,解决了证据冲突,取得了更客观的融合结果。

(3)实验结果表明,本文所提方法能够有效解决证据冲突问题,提高了临近空间飞行器遥测数据相关性分析结果的可信度。