在知识探究中培育数学素养——以《平行四边形的面积》为例

文|李振新 张亚兰

【教学内容】

青岛版五年级上册第65～68页。

【教学重、难点】

探索并掌握平行四边形的面积计算公式的推导历程，会灵活运用平行四边形的面积计算公式解决问题，初步体验转化思想。

【教学准备】

课件、平行四边形纸片、剪刀、尺子、透明方格板（每小格为边长1 厘米的正方形）等。

【教学过程】

一、结合情境，回顾旧知

师：同学们，施工队运来一块玻璃，它的形状是什么图形？

生：长方形。

师：还记得长方形面积的探究过程吗？

生：我记得用面积是1 平方厘米的小正方形纸片铺一铺，然后数一数一共铺了多少个小正方形，最后得出结论：长方形的面积等于长乘宽。

师：学得真不错！现在施工队要将一块长方形的玻璃切割，为楼梯装上玻璃护栏，在这个过程中，图形的面积发生了什么变化？

生：切割后图形的面积会变小。

师：这是用切割出的所有小玻璃块重新拼摆的图案，它的面积和原来长方形的面积有什么关系？

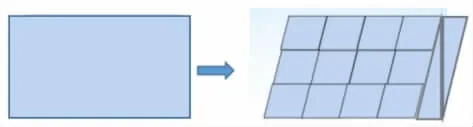
生：它们的面积相等。

师：这是我国古代数学家刘徽发现的“出入相补”原理：图形分割后重新拼摆，面积保持不变。

师：今天要借助这个原理，探究平行四边形的面积。

（板书：平行四边形的面积）

二、迁移猜想，实验验证

师：大家猜一猜，它的面积是多少？（板书：猜想）

生：7×5=35（平方厘米）。

［板书：7×5=35（平方厘米）］

师：说说你的想法。

生1：我知道长方形的面积是长乘宽，所以我猜平行四边形的面积是相邻两边长相乘。

师：合理的猜想。猜想是研究的第一步，接下来我们需要——

生：验证。

师：怎么验证？（板书：验证）

生：用“铺一铺”的方法。

师：和老师想的一样。不过，这次老师给大家带来的是这个（出示透明方格板），里面的每个小方格是1 平方厘米，知道怎么用吗？大家借助它数一数这个平行四边形的面积吧。

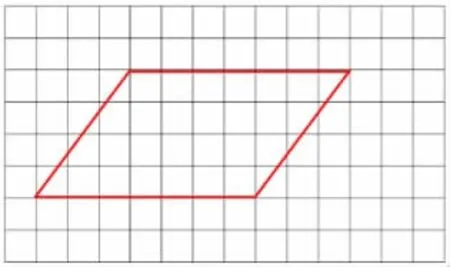
师：有结果了吗？

生：28 个格子，28 平方厘米。

师：你是怎么数的？

生：满格的一共22 个，把不满的格子合在一起，凑成6 个满格，所以一共是28 个格子，也就是28 平方厘米。

师：你发现了什么？

生：和之前的猜想不一致，我们猜得不对。

师：验证否定了之前的猜想，看来我们的研究不是一帆风顺啊，但是我们要迎难而上，继续探究！（板书：探究）

三、合作探究，创生新知

1.初步推理，再行猜想。

师：原来只要数格子，就能知道图形的面积。你觉得这种方法怎么样？

生：太麻烦了，要一格一格地数。

生：还可能遇到很多填不满的格子，合在一起很麻烦，也不够准确。

师：确实需要一种简单的方法，最好像计算长方形的面积那样，一下子就能算出来。

生：老师，我在数格子的时候发现，这个平行四边形的高是4厘米，底是7 厘米，4×7 正好是28平方厘米。

师：所以你想说？

生：我猜会不会是“底×高”？

师：这个发现好像有些道理，7×4=28（平方厘米），和我们数格子得到的结果一样。那么它到底是一个真理，还是一个巧合呢？依然需要我们进行验证。怎么验证呢？

师：还记得前面老师提过的“出入相补”吗？将几何图形切割后重新拼摆，面积怎样？

生1：面积不变！

生2：我想将平行四边形分割，然后重新组合。

师：你打算组合成什么图形？

生2：可以组合成长方形或者是正方形。

师：为什么要组合成长方形呢？不能转化成别的图形吗？

生：因为我们知道怎么算长方形的面积，算起来比较方便。

2.操作探究，合作交流。

师：你们想将平行四边形转化成长方形，将未知的知识转化成已经学过的知识，许多的新知识就是这样被发现的。平行四边形是否能转化成长方形呢？老师为大家准备了平行四边形小纸片和剪刀，请大家打开学具袋1，小组合作探究。

师：哪个小组来分享一下你们的研究成果？

生1：沿着平行四边形的高剪开，剪下一个三角形，将三角形平移到右边，就是长方形了。

师：这个小组的同学成功完成了转化，谁还有不同的想法？

生2：我们小组和他们的方法不同。

生2：他们是沿着从顶点作的高剪开，我们是沿着中间的高剪开得到两个梯形，然后重新拼在一起，组成长方形。

生3：菱形小纸片，将它沿着顶点的高剪开，也能拼成一个长方形。

生4：我们小组也是沿高剪开，重新拼摆，将平行四边形转化成了正方形。

生：我觉得只要沿着平行四边形的高剪开，就能拼成长方形，而平行四边形有无数条高，所以我觉得应该有无数种方法。

师：你们同意吗？

生：同意。

师：为什么一定要沿着高剪开呢？

生：因为转化成长方形，必须要有直角，沿着高剪开，才能得到直角。

师：有道理！沿高将平行四边形分成两部分，再平移，就能把平行四边形转化成长方形。

3.寻找联系，创生新知。

师：转化前后的图形之间有什么联系吗？根据这个联系我们能不能推导出平行四边形的面积计算方法呢？小组一起探讨一下。

（小组探讨，教师巡视）

师：哪个小组能交流一下你们的想法？

生1：根据“出入相补”原理，我们发现转化后的长方形的面积和之前平行四边形的面积相等。

生2：而且长方形的长就是原来平行四边形的底，宽就是平行四边形的高。

生3：长方形的面积计算公式是长×宽，所以平行四边形的面积计算公式就是底×高。

生4：是的，这和我们之前的猜测是一样的。

师：小组内互相说一说转化的过程。

师：你们真厉害，通过合作探索，转化推理，得出结论：平行四边形的面积=底×高，用字母表示为S=ah。（板书）

四、巩固拓展，素养提升

1.计算下面图形的面积。

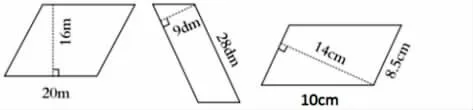
师：最后一道题目，究竟是10×14，还是8.5×14？

生1：我认为都行，10 厘米和8.5 厘米都是底，14 厘米是高。

生2：这样算出来的结果不一样啊。

生3：我认为是14×8.5，因为它们是互相对应的底和高。

师：我们在推导小玻璃块的面积时，都是以7 厘米的边为底，沿着它的高剪开的，大家有没有想过，以5 厘米的边为底呢？请大家认真看大屏幕。

（播放微课视频）

师：你发现了什么？

生：我发现了5 厘米的底乘5.6厘米的高，也等于28 平方厘米。

师：和我们之前学的不一样吗？

生：是一样的，都是底乘高，但是这是另一组底和高。

师：是的，计算同一个平行四边形的面积理论上来说有两组数据，因为平行四边形有两组相对应的底和高。用哪组数据计算，要根据具体题目，具体分析。

师：同学们，关于上面的题目，你有答案了吗？是什么？

生：8.5×14。

师：这就提醒我们什么？

生：计算面积时要注意底和高相互对应。（板书：底和高相互对应）

2.请你填一填，再结合图示，叙述转化过程。

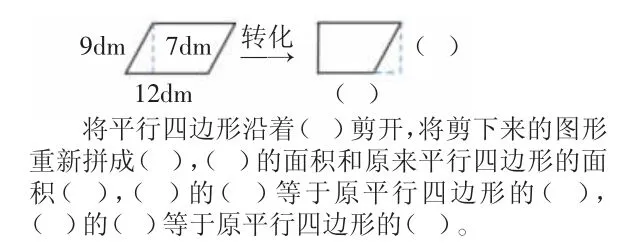
3. 计算下面平行四边形的面积，你能发现什么？

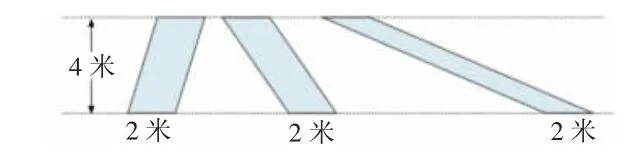
生：这几个平行四边形的面积相等。

师：它们有什么共同点？

生：底相等，高也相等。

师：所以等底等高的平行四边形，面积相等。（板书：等底等高，面积相等）

师：同学们再来看这幅图，有什么发现？

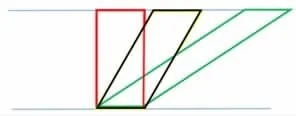
生：这也是等底等高，这三个图形的面积是相等的。

师：你能不能画出和上面图形面积相等的平行四边形？

生：可以，只要保证等底等高，平行四边形的面积就相等。

师：你能画出多少个？

生：很多个。

师：理论上应该是无数个，画一画试试吧。

五、总结概括，全面提升

师：同学们，这节课你有什么收获？

生1：我知道了平行四边形的面积计算公式是底乘高，而且底和高要相互对应。

生2：我知道平行四边形的面积计算公式的推导过程，是将平行四边形转化成长方形，长方形的长就是平行四边形的底，宽就是平行四边形的高。

生3：我体验到了探究的乐趣，先猜想，再验证，猜得不对就继续猜想、探究和验证，最终得出结论，这个过程让我很有成就感。

生4：我会画很多个面积相等的平行四边形，因为只要保证它们等底等高就行。

师：很高兴大家收获如此之多，有知识的收获、体验的收获，还有思维的拓展。最后，你们想不想知道，谁是最早用“出入相补”原理研究平面图形的面积的？

（微视频向学生介绍刘徽的“出入相补”原理）

师：看了视频你们有什么感想？

生：我觉得刘徽太厉害了，用“割补法”解决了很多几何问题。

师：同学们，你们也可以做到，你们就是小小数学家。