挖掘学习深度促进思维跃迁
——拓展课《平行四边形的等积变形》教学设计
文 何佳丹
【教学内容】
人教版五年级上册第86 页。
【教前思考】
下图为人教版教材平行四边形面积新授课后的一道习题。两个平行四边形同底,根据平行线间的距离处处相等,它们的高也相等,所以面积相同。这个问题通过观察,不难解决,但其实像这样等底等高面积相等的平行四边形还有很多,明白等积变形背后的道理,这个性质还可以推广到后续三角形、梯形甚至更多的平面图形面积中,实现从题教到类教。 因此从此题入手,整体考虑不同学生的认知基础,深度整合相关习题,尝试改一题为一课,从典型的长方形入手,逐渐将学生头脑中关于平面图形的认知有序联系,引导学生操作实证,多向思考,把握平行四边形等积变形本质。

【教学目标】
1.经历深度操作,画面积相同的平行四边形的过程,在独立思考中培养分析推理能力,在动手操作中感悟等积变形思想,发展空间想象力。
2.推理验证等底等高的平行四边形面积相等,以及利用积的变化规律解决平行四边形面积的相关问题。
3.用数学学习活动,感悟数学知识前后联系,进一步渗透“转化思想”,发展迁移应变能力。
【教学准备】
教师准备:课件、几何画板动态演示图。
学习材料:格子图、彩笔、剪刀、三角尺。
【教学过程】
一、直观操作,探索新知
师:前面我们学习了平行四边形的面积,今天我们继续研究平行四边形面积里的奥秘。
1.自由画: 激活已有经验。
活动一:“画”面积相等的平行四边形,激活知识经验。
要求:自己想办法,画出和长方形面积相等的平行四边形,看看你能画几个。(学生画三分钟)
2.交流反馈:展示经验思考。
师:你们画的平行四边形和长方形面积相等吗?

生:长方形是特殊的平行四边形,还可以画面积也是12 的其他长方形。
生:长方形的面积是:2×6=12,就去想想( )×( )=12。
生:画和长方形等底等高形状不一样的平行四边形,底边都是2,高都是6,2×6=12,所以面积相等。
生:平行四边形和长方形底和高都相等,根据面积公式,可以确定乘积也相等,所以面积相等。
师:大家想到的办法可真多,通过具体数据的计算,根据面积公式底乘高,验证了等底等高的平行四边形面积相等。
二、推理分析,实证明理
师:大家想到的办法可真多,通过具体数据的计算,根据面积公式底乘高,验证了等底等高的平行四边形面积相等。
1.验证发现:等底等高,面积相等的平行四边形有无数个。
(1)图形实证:等底等高,面积相等。
活动二:剪拼证明:为什么等底等高的平行四边形面积相等?
师:这两个图形形状很不一样,还有办法可以验证它们的面积相等吗?拿出信封里的材料,自己动手试试看。
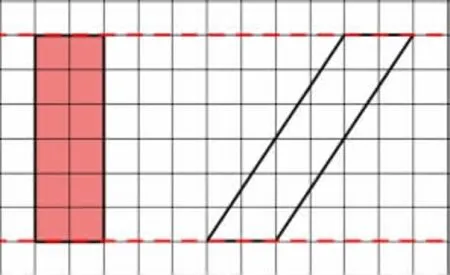
操作:学生尝试对右边的平行四边形画、剪、拼。
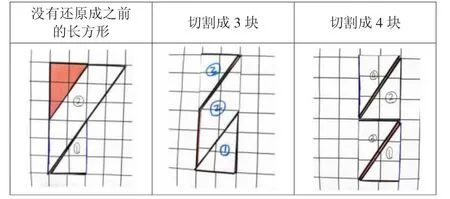
图10 图形实证面积相等的示意图
生:我剪成了两块,①号与其中部分重合,剩下的②号和长方形剩下的一样大。
生:你的看不出来面积相等。我再剪一次,分成三部分重新拼,刚好和长方形完全重合。
生:我剪成4 个完全相同的三角形,重新拼后和长方形完全重合,说明面积相等。
师:原来将平行四边形多次割补转化成左边的长方形,就能一眼看出等底等高的平行四边形面积相等。
师:现在把将这个图形平移过去,你还有新的发现吗?

生:除了公用部分,剩下两块图形的面积也相等。
(2)再次画图:发现等底等高的平行四边形有无数个。
活动三:快速画:筛选最佳策略。
要求:来个小小的比赛(2 分钟计时)。看谁的速度最快,画出尽可能多的和长方形面积相等的平行四边形。
师:用手势告诉我你们画了几个?
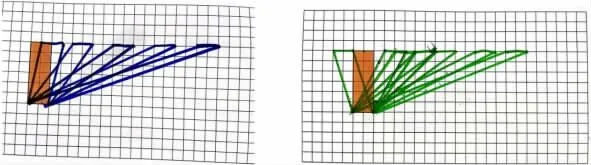
师:你们现在怎么一下子画出了那么多个?
生:共用已有平行四边形的一条底边,可以节约画一条边的时间。根据平行线之间的距离处处相等,高也就相等了。将上面的底边不断向右移动就可以了。
生:上面的边也可以往左边方向平移。
师:如果格子图足够大,时间也足够多,你能画多少呢?
生:无数个。
小结:等底等高的平行四边形不仅面积相等,且有无数个。
2.双向辨析:深刻把握等积变形本质。
(1)逆向反思:面积相等的平行四边形,一定是等底等高吗?
生:不一定,比如底3 高4 的平行四边形。
小结:面积相等的平行四边形,不一定等底等高,也有不等底不等高的情况。
(2)再次思考:不等底、不等高的平行四边形一定面积相等吗?如何保证?
生:只要底和高的乘积都是12 就可以。
生:平行四边形面积=底×高,底和高就是两个因数,利用积不变规律,一个因数乘几另一个因数就除以几(0 除外),也可以保证。
师:真棒,利用积不变规律,就能保证面积相等。
小结:不等底不等高的平行四边形,底和高乘积相等时,面积相等。
(3)想象整理,在平行四边形等积变形中渗透极限思想。
师:现在我们找到了5 个不等底、不等高但面积相等的平行四边形。还有吗?
生:2.4×5、24×0.5。
师:如果底是0.6,高就是?底是0.06,高是?底是0.006,高是?
小结:不等底、不等高但面积相等的平行四边形有无数类。
师:如果用一生的时间去画面积是12 的平行四边形,你画的完吗?
生:画不完。
小结:等底等高,面积相等的这一类平行四边形有无数个。不等底、不等高面积相等的平行四边形有无数类。
三、变式练习,拓展应用
练习一:正方形的周长是32cm,你能求出平行四边形的面积吗?
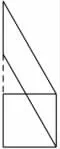
生:平行四边形的底和高就是正方形的边长。
师:关于这个问题有不同的想法吗?
生:这两个图形等底等高,面积相等,求平行四边形的面积就是求正方形的面积。
练习二:如图,长方形框架面积是400cm2,把它拉成一个平行四边形,长方形的高度是平行四边形的2 倍。拉动后的平行四边形的面积是多少?
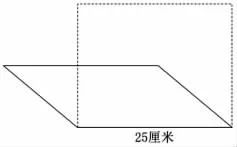
生:先算出平行四边形的高,再求面积(400÷25)÷2×25=200(cm2)。
生:等底,高是2 倍,对应面积也是平行四边形面积的2 倍:400÷2=200(cm2)。
师:如果继续拉动,长方形的高度是平行四边形的4 倍,对应平行四边形的面积是多少?
生:长方形面积是平行四边形面积的4 倍。
师:n 倍呢?
生:长方形面积是平行四边形面积的n 倍。
小结:等底,高的倍数关系和面积的倍数关系一样。 高是现在的几倍,面积也是现在的几倍。
对比反思:对比一下,这个问题,和刚才研究的内容,一样吗?
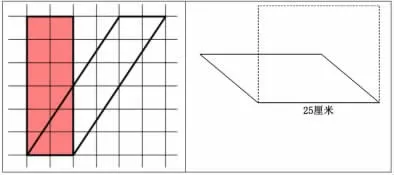
生:之前研究的是等底等高,面积相等,等积变形。现在这个问题是等底,高不同,面积也不同,相同的是周长,等周长变形。
师:是的,解决问题之前,我们要先观察,思考判断属于哪种情况。
四、回顾反思,提炼经验
师:这节课你有哪些收获?
生:我掌握了等积变形的方法:可以利用等底等高画出无数个面积相等的平行四边形。
师:这是个不错的方法。
生:也可以根据积不变规律。我还知道有的信息正向思考结论是对的,反过来就不一定了。
师:已知信息推理出的结论,有时候并不能作为条件反推。学习完还有新的问题吗?
生:其他图形中也有可以用这些方法进行等积变形的吗?
师:你提出了一个很好的问题,等我们学习了更多的平面图形的面积后可以继续探究。
——课堂的民主集中制

