杨传冈老师“平行四边形的面积”教学设计片段


一、谈话引入
1.回顾:这里有一组公园里花圃的图片,这些花圃的形状有你熟悉的图形吗?
2.启发:(出示长方形、正方形)你会算这两幅图形的面积吗?(从没有具体数据到有小方格,每个方格边长1厘米)三年级时用数方格的方法推导出了长方形、正方形的面积计算公式。
3.揭题:(出示一个平行四边形)它的面积又该怎样计算呢?这就是本节课要研究的内容。(板书:平行四边形的面积)
【设计意图】课始,给学生一个开放的游玩场景,让学生从熟悉的图片中回顾已学图形,激活学生用数方格的方法推导长方形、正方形面积的方法记忆,为学习新课做好铺垫。
二、方法探究
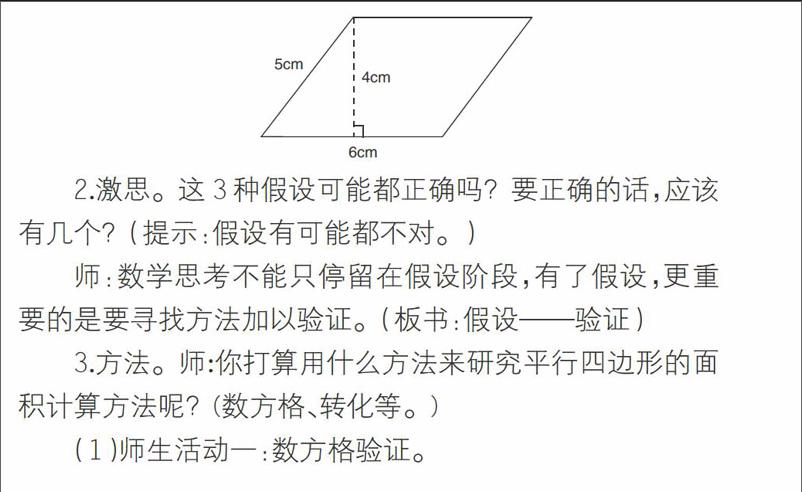
1.设疑。师:猜想一下,这个平行四边形的面积可能会用哪个算式来计算呢?(6×5,6×4,5×4)
2.激思。这3种假设可能都正确吗?要正确的话,应该有几个?(提示:假设有可能都不对。)
师:数学思考不能只停留在假设阶段,有了假设,更重要的是要寻找方法加以验证。(板书:假设——验证)
3.方法。师:你打算用什么方法来研究平行四边形的面积计算方法呢?(数方格、转化等。)
(1)师生活动一:数方格验证。
第一层次:验证第一、第三种假设。
学生小组合作,通过铺、摆1平方厘米方格的办法排除5×4,6×5两种可能,教师指导学生深究错因,逼近知识本质。
第二层次:验证第二种假设。
指导学生先去掉多余部分,再将图形内的零碎部分剪、切、移、拼成整格,从而直接数出面积数量(如上图)。
初步结论:24个小正方形正好铺满这个平行四边形,平行四边形的面积为24平方厘米。(6是平行四边形的底,4是这条底所对应的高)现在,你知道平行四边形的面积怎样计算了吗?板书公式。
方法回顾:用先假设再验证的方法得到了平行四边形的面积计算方法是底乘高。
师:有一位科学家却认为,只用一种方法来证明一个结论还远远不够,还可以怎样证明?
(2)师生活动二:转化法。
第一层次:思想渗透。
下面两个图形面积相等吗?
学生猜测后电脑验证,教师启发方法。(通过转化,把不规则图形通过剪、移、拼,转化成长方形,面积不变。)
第二层次:数据实证。
(1) 操作实验。
你能把一个平行四边形转化成长方形吗?
活动小贴士:
① 选一选:从信封中任意选择一个平行四边形。
② 说一说:小声商量一下,我们小组准备怎样转化。
③ 动动手:两人一组,剪一剪、移一移、拼一拼,我们有什么发现?
小组活动,展示交流(突出展示剪法不同,转化效果相同,即通过剪、移、拼,把平行四边形转化成了长方形)。
师:开普勒说过,数学就是研究千变万化中不变的关系。
(2)数据整理
对照上表中数据,讨论并回答教科书第8页的三个思考题。
(3)梳理结论(边梳理边板书):
(4)描述历程:谁能说一说,平行四边形的面积是怎样推导的呢?
(5)字母表达:S=a×h。
【设计意图】受长方形面积计算方法的定式思维的干扰,不少学生认为平行四边形的面积等于相邻两条边的乘积,这是学生认知中最大的障碍。为了突破这个难点,教师对教材进行了大胆重组,放开手脚让学生在猜想验证中自主探索,研究思路多元,研究方法开放。学生通过摆小方块探究,逐一排除,初步得出平行四边形计算方法;再用转化法先操作后根据数据从两个层次由表及里展开实证,层层剥笋直抵知识本质,建立平行四边形面积计算的方法模型。教师从层层递进中追根溯源,不断释疑明理。这种回归思维原点的做法,让学生在开放探究中深刻感悟到数学的本质,体验到探索与发现的快乐。最终实现基础知识习得、基本计算技能练习、数学思想方法渗透、基本活动经验积累的四位一体的有机达成。
(作者单位:江苏省盐城市第二小学)
责任编辑:周瑜芽
Email:jxjyzyy@163.com

