高中数学与体育的跨学科教学研究

林晴 赵玲燕

【摘要】在新课标指导下，教师要分析体育运动学校体育生数学学习困难的原因以及跨学科教学现状，接着将足球、田径、乒乓球等体育项目知识与高中数学面积、集合、三角函数、分段函数、概率与统计知识结合，进行跨学科教学设计，帮助体育生在熟悉的训练情境中提升数学解题能力和核心素养，激发对数学学习的兴趣。

【关键词】高中体育生；数学跨体育学科教学；教学设计

体育特长生是我国体育后备人才的重要组成部分之一，这一群体的文化素质不仅关系到国家体育领域运动员的整体素养，而且对其高三参加单项或普通招生考试升学也至关重要，因此，如何运用合理的教学方式提高体育特长生的数学学业成绩和改善学习态度就成为了亟待解决的问题。

由于STEAM教育理念的产生和发展，高中数学教学中也逐渐出现科学、工程、技术与艺术知识，为数学教师实施跨学科主题教学提供了丰富的素材，例如在二次函数及一元二次方程、不等式这一章出现了汽车刹车、花坛设计、风暴预报、居民小区休闲广场设计等相关知识；在第三章函数性质知识学习板块出现玻意耳定律、烟花高度、心率测定等相关知识。

以上跨学科教学部分都通过构造一些生活中的真实情境或引用一些相关学科领域的知识来辅助学生理解与掌握数学知识，一定程度上促进了学生的数学学习水平，激发了学生数学学习兴趣。同样的，体育生在面对抽象难懂的数学知识时，如果将他们置身于熟悉的体育训练或比赛场景，对他们的数学学习也会有帮助。对于其他普通学生，体育情境下的数学学习也会激发他们对体育项目的兴趣。

一、高中数学与体育跨学科教学的设计

世界著名数学教育家弗赖登塔尔认为情境问题是教学的平台，数学化是数学教育的目标，学科交织是数学教育内容的呈现方式。在传统课堂中数学教学常常按照科学的体系展开，许多例子脱离生活实际，不太重视学生自己的数学生活经验，因此学生没有办法很好地掌握新授知识，更无法利用数学在现实中进行再创造，而弗赖登塔尔倡导使用直观的、易于引起想象的情境问题。对于体育特长生而言，应该从他们感兴趣且熟悉的体育项目出发，在课堂中设计数学与体育学科交织的真实情境问题，适当改编课本中的例题，并设计综合多个数学知识的课外讲座等，尽量让他们减少对数学的恐惧和隔阂，感受到数学就在生活中，在他们日复一日的体育训练中。

1.初高中衔接课设计

以海口市体育运动学校为例，本校的体育生升高中时学科基础薄弱，许多初中的数学知识都未完全掌握，因此在讲解高中课程之前，需要花半个学期的时间来进行初中知识的复习巩固，与高中知识进行衔接。在部分衔接课中设计了结合学生复习内容、以足球为主线的跨学科教学内容—足球点球中的数学。

在课堂引入时，先给学生播放2022年卡塔尔世界杯阿根廷对战荷兰的点球大战视频，调动学生的積极性和注意力，接着让所有学生在纸上写下自己认为的点球命中率进行竞猜，看看这节课结束后谁的推测更加接近结果。首先，我们要对这一问题进行数学建模，用数学的眼光去分析点球问题。对于刚上高中的体育生，选择最简单的幸运游戏模型，该模型假设射手只可能将球射向球门四个角的其中之一，而守门员就要提前预测并扑向其中一角，因此每一个点球对于射手和守门员而言都是一次幸运游戏。那么此时的命中率是多少呢？由初中学习的概率知识可知是75%，如果是在射手还有可能踢向门中间的情况下，命中率就会上升到80%。进一步解释如果将该模型精化，合理的命中率会在70%到80%之间。

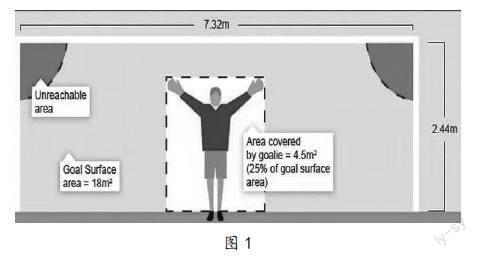
除了幸运游戏模型，还可以用面积法来计算命中率。已知规范的球门面积为17.86平方米，那么一个守门员用他的手脚能覆盖多少面积？可以先让学生进行讨论猜想将守门员的防守范围抽象为图形，最后教师给出其中一种假设—守门员的平均身高1.9米，臂展为1.9米，肩膀离地约1.6米，双脚打开与肩膀同宽，那么守门员手臂扫过的区域相当于半径为0.95米的半圆，身体相当于长方形。（如图1）

由此假设，计算防守面积为，那么守门员的防守比例大约为25%，即射手命中率约为75%。课后还可以让同学们测量自己的身体数据进行计算，假设自己是守门员，能防守住多少球门面积。

以上两种算法可以帮助学生在衔接课中复习到长方形和圆的面积计算、概率等方面知识，还培养了数学建模、数学运算、数学抽象等核心素养，让学生发现简单的数学知识也可以用来解释足球训练中的一些现象，对数学学习更感兴趣。

2.集合专题设计

一上高中，学生首先要面对的就是第一章集合与常用逻辑用语，集合不仅与之后学习的函数、概率与统计等有关联，而且经常作为高考、体育单招考的第一题出现，因此非常重要。在集合间的基本关系和集合的基本运算教学过程中，可以设计以下例题。

例1：集合间的基本关系

（1）集合A是高一（1）班的篮球队队员的集合，B集合是高一（1）班的全体学生，说出两个集合之间的关系；（2）举出下列集合的子集（答案不唯一）：A={x│x是高一所有训练队}，B={x│x是高一（1）班所有足球队员}；（3）高一（1）班所有橄榄球队队员组成的集合。

设计意图：第一小问用本班体育生的实际情况，帮助学生理解子集与真子集的概念，第二小问则是考察学生在理解知识基础上的应用，第三小问的前提是本校不设有橄榄球队，利用此考察空集知识点。

例2：集合的基本运算

（1）A={x│x是高一（1）班所有女生}，B={x│x是高一（1）班篮球队队员}，求出两个集合的交集；（2）C={x│x是高一（1）班田径男队员}，D={x│x是高一（1）班田径女队员}，求出两个集合的并集；（3）假设高一（1）班举重队有a，b，c，d，e五位同学，，F为高一（1）班全体举重队员，求集合E相对于全集F的补集。

设计意图：通过三个跟运动队有关的问题帮助体育生理解交并补的概念，同时例子中不同队伍的变换让更多数的体育生都有参与感。

3.函数专题设计

（1）三角函数。在学习三角函数诱导公式的过程中，我们可以引入足球赛场情境，激起体育生的学习兴趣。在足球比赛的传球过程中，有时候球员会把球踢得很高，让球能在空中停留足够长的时间，好让队友有足够的时间跑到理想位置接球，尤其是他们希望将弧形任意球或角球踢进球门区域，这样队友会有更多时间聚集到有威胁的进攻区域。假设以速度v、与地面成角踢球，不考虑空气阻力等因素，它的飞行轨迹是抛物线，飞行距离为

，当达到最大值1时，飞行距离R也达到最大值，如果给定一个球员希望传球给队友的球飞行距离，也就是R为定值时，可以如何实现精准传球的目标？由我们的诱导公式可知，，也就是发射角和能达到的射程是一样的，但高开球在空中停留的时间更长，如果队友已经就位，在对手赶到之前可以选择两者中小的发射角，反之如果要拖延时间，可以选择大的发射角让空中时间延长，这就是传球中的三角函数。

（2）分段函数。虽然体育生每天在田径场上锻炼体能，但是他们大多数并不知道田径场的设计中也蕴含着函数知识，因此在学习分段函数时，我们可以利用田径场的平面图进行引入，在平面直角坐标系中构造四百米跑步的数学模型，为了简化计算，只写出内圈跑道上半部分对应的分段函数解析式，π取3.14计算。

弧形部分的长度为2×3.14×36.5=229.22m，总跑道为400m，那么剩下的每条直跑道就为85.39m。

当0≤x≤36.5时，圆的方程为（x-36.5）2+y2=36.52，对应跑道的解析式为；当36.5≤x<121.89时，对应跑道的解析式为y=36.5；当121.89≤x≤158.39时，圆的方程为（x-121.89）2+y2=36.52，对应跑道的函数解析式为。

综上，400米跑道内圈上半部分的函数解析式和图像（见图2）。

从力学的角度分析，直线恰好为圆弧在临界点处的切线时，在一定程度上可以让运动员在转弯时身体更好保持平衡，由此让学生体会到在进行田径场地设计时，运用好数学原理可以帮助运动员更好地进行训练和比赛。课后可以让学生查阅资料、举一反三，发现生活中哪些体育场馆、体育器具的设计也蕴含了数学原理，完成作业并在之后的课上交流。

4.概率与统计专题设计

在很多体育比赛的队伍分组、选人、赛制、比赛情况和战略中，都涉及到高中部分统计和概率的知识，以下列举一道在体育主题背景下的概率与统计例题。

例：（回归直线与线性相关系数）首先为了计算的简便，我们只给出运动员卡尔利普在1986～1989年的本垒打数据，以此来拟合回归直线并预测1990年的本垒打次数并计算线性相关系数。

解：设回归直线方程为=b+mx，其中m为直线的斜率，b为y轴上的截距。

，

所以有

。，因此回归直线为。

由于在总表中给出的是该运动员1981～2001年的数据，此处只摘出了部分年份的成绩，因此在总表中1990年相当于x=10时，代入方程可得，总表中1990年卡尔利普真实的本垒打数据是21次，可见预测值与真实值很接近。

最后计算线性相关系数为

≈-0.8004，因为回归直线的斜率为负，-0.8004说明点与直线有合理的相关性。

除此之外，体育场馆鸟巢的设计中蕴含着如何用直线簇构造出椭圆的知识，足球高吊球、篮球后仰跳投中含有抛物线的原理，运动员体内药物存留量随着时间的变化可以得到通项公式，调和数列可以用来估计100米赛跑世界纪录的极限，构造函数模型可以模拟运动员百米赛跑的速度变化，等等。这些鲜活的体育案例都可以帮助体育生提升解决问题的能力和信念，让他们对体育的热爱转化为学习数学的最佳动机，进而循序渐进，主动学习。

在教学实践环节，笔者发现体育运动学校的学生在课堂上更喜欢这些有体育背景的问题，更乐意在这样的课堂氛围中进行问题的思考与探讨。完成課后作业时，也会对融入了体育知识的数学习题态度更加积极。在高中数学课堂中融入体育学科知识，不仅能使体育生学习数学的热情高涨，也能引起普通高中的文化生对体育的兴趣，部分学生在课余时间也许会因此而想要进行更多更丰富的体育运动，进而在智育的同时达到体育的目的。

【参考文献】

[1]马蒂亚斯·路德维希.数学与体育—数学视角下的奥林匹克项目[M].徐斌艳，译.上海：上海教育出版社，2020.

[2]约翰·D·巴罗.体育中的100个数学问题[M].周启琼，靖润洁，译.上海：上海科技教育出版社，2021.

[3]罗纳德 J.古尔德.让你爱上数学的50个游戏[M].庄静，译.北京：机械工业出版社，2020.