章头课教学探索

王星

摘 要： 一元一次方程是初中阶段“数与代数”部分的重要内容，也是数学中的基本运算工具，对学生培养分析问题、解决问题的能力、体会数学的价值具有重要意义.同时，一元一次方程也是以后学习二元一次方程组、一元一次不等式（组）及一元二次方程的基础，是刻画现实世界中数量关系重要模型.章头课是对一章内容的概括，通过学习，学生可以初步了解到本章将要学习的内容、研究的方向，构建知识结构框架，更加系统和有条理地完成新的一章的学习.

关键词： 一元一次方程；章头课；思考

我有幸受邀执教了一节苏科版七年级上册第4章“一元一次方程”的章头课，这次活动让我对章头课有了初步的认识与思考，现将几点认识及思考总结如下，与同行分享.

1 教学内容解读

蘇科版教材每章的开头部分都设计安排了“章头语和章头图”.章头课作为一章内容的起始课，涵盖了整章的学习内容、思想方法，就“一元一次方程”而言，教材安排了飞驰的赛车和平衡的天平作为章节开头的素材，章头语为：方程，表达数量之间相等关系的“天平”，是解决实际问题的有效模型.章头语简洁明了，章头图丰富多彩，两者是本章的重要组成部分，它们体现了数学在生活中的应用价值.教材用一动一静两幅图来表达这种数量的相等关系，说明方程是分析解决问题的有效工具.右边的天平平衡图用2x+125表达了质量和砝码之间的数量关系.让学生感受到数学语言在生活中的应用.

一元一次方程是学生进入初中后接触模型思想的第一课，学生需要了解方程、一元一次方程有关概念，理解等式的性质，基本了解本章学习内容和知识框架，经历一元一次方程解概念形成与初步探究解一元一次方程的过程，体会模型的思想和从特殊到一般的数学思想.笔者反复斟酌教材的编写意图，设计了如下的教学过程：

2 课堂教学及说明

2.1 设计情境，贴近生活

活动一：  年龄的问题

刚刚我与这位同学交流了一下，发现我的年龄是他的三倍还多8岁，你能用所学的代数式来表示年龄关系吗？若知道我今年44岁，你能求出这位同学的年龄吗？这样的等式你能自己编一个吗？如：几年后我俩年龄之和是100岁？几年后我的年龄恰好是这位同学年龄的3倍？

设计意图：  好的课堂一定是学生自主的课堂，通过交流年龄问题不仅可以活跃气氛还可以直接引入主题，而且还可以提升学生的注意力，激发学生的求知欲，促进学生的积极思维，同时很自然地引出了方程的相关内容，让学生感受从代数式到方程的形成过程.

2.2 尝试练习，形成概念

活动二：  糖果的问题

1. 老师给积极回答问题的同学准备了棒棒糖，每人分4个则少6个，如果每人分3个则多4个，你能知道老师准备给多少名学生发棒棒糖？带了多少个棒棒糖吗？

2.  已知桌子上有两盒棒棒糖，共50支，我从第一盒里拿 10 个放进第二盒，两盒棒棒糖就一样多了.你能知道原来每个盒子中各有多少个棒棒糖吗？

活动三：

你能自己列举出生活中具有等量关系且用这种等量关系解决问题的实例吗？

设计意图：  通过学生切入实际的思考后形成4x-6与3x+4的代数式，体会用不同的方法“算两次”，然后用“=”连接，然后通过类比的方法得到4x-6=3x+4，x-10=50-x+10等式，学生在问题串的引领下有序思考，为学生探究方程指明方向，让学生感受由未知到已知，从陌生到熟悉的探索过程.

2.3 尝试练习，形成概念

利用课本习题图进行追问：

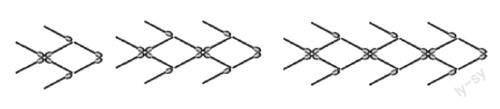
搭1条，2条，3条“小鱼”各用多少根火柴棒？按同样方式，搭20条“小鱼”要用多少根火柴棒？

反之，我若给你140根火柴棒你能搭多少条小鱼呢？

设计意图：  通过学生熟悉的“小鱼”问题结合刚刚的含有未知数的等式，形成如下定义：只含有一个未知数且未知数的次数都是1次的整式方程叫一元一次方程.此处是课堂的高潮之一，因为学生在上课过程中竟然抢着写，并且有学生主动提出尝试写一元二次方程与二元一次方程等，笔者在点评学生回答的同时形成板书，增加印象，并为后面的学习做好铺垫工作.

2.4 依据经验，尝试解法

丢番图被认为是代数学的鼻祖，但历史上没有一本正式的著作里留下他完整的生平，甚至连他的国籍都没有明确的记载.然而有趣的是，他竟然有一个墓志铭，上面镌刻着他的一些情况：“他生命的六分之一是幸福的童年.再活十二分之一，颊上长出了细细须.又过了生命的七分之一才结婚. 再过五年他感到很幸福，得了一个儿子.可是这孩子光辉灿烂的生命只有他父亲的一半.儿子死后，老人在悲痛中活了四年，结束了尘世的生涯.” 你知道丢番图结婚时和去世时的年龄分别是多少吗？

设计意图：  通过对4x-6=3x+4的分析，初步认识了方程的解及解方程并能利用等式的基本性质初步解简单的一元一次方程.此处让学生经历感受、猜想、验证、探究、应用的过程，让学生感受解的本质，引发兴趣为学生后续深入学习做铺垫.

当堂反馈

1. 下列方程中，是一元一次方程的是（  ）.

A.  x2-4x＝3

B.  xy-3＝5

C.  3x-1＝ x 2

D.  x+2y＝1

2. 在日历纵列上圈出了三个数，算出它们的和，其中正确的一个是（  ）.

A.  28

B.  34

C.  45

D.  75

3. 由“比a的3倍大5的数等于a的4倍”可列一元一次方程：      .

4. 解下列各方程：

（1） 3（x-1）＝6；

（2） 2x＝9-x.

设计意图：  进行适时反馈训练是提升教学效果的有效手段，此处用4个不同类型的题目讓学生从定义、形象应用，抽象感知、方程求解展开练习.让学生感受到使用方程模型的方便简捷.

2.5 课堂小结

本节课发现了现实问题中隐含的方程，并对发现的方程进行了研究，参照本节课的研究思路和方法，对之后的学习内容你准备如何研究？

设计意图：  在学生总结感悟的基础上进行这样的提问能有效地形成知识框架，并让学生形象地感知下面的学习内容，体现了这节章头课的可延展性和可生长性，培养了学生的探究意识与探究能力，让学生体会学无止境.

3 教学感悟

章头课是对一章内容的概括，通过这节课的实践教学，笔者在实施教学时有以下几点感悟：

1. 章头课的实践教学能有效提高教师对教材的理解能力与再处理能力，笔者研究教材的设计发现从字母到数，从数到式，从式到方程，从方程到不等式、函数都是一条线串起来，我们课堂设计如何用一条线串起来？这是我们备课的重点.

2. 章头课的教学是单元教学的基础与实践，而单元教学能有效提升教学成绩要上好单元教学课，教师应从章头课的研究做起，建立起知识体系，为后续的学习创设好框架与方向.

3. 章头课的教学不追求教学内容的多少，而在于让学生形成框架结构、数学模型以及感受数学模型应用的必要性与便捷性.教学以提高数学能力，形成问题意识，发展深度思维为主要方向.本节课的一元一次方程教学就以活动的形式逐步展开，以问题贯穿整个课堂，让学生感受数学模型应用的必要性与便捷性.

4. 章头课的教学适宜开门见山，然后进行转化，从一个生活情境引入，让数学知识源自生活，高于生活，让学生感受一元一次方程概念的形成过程，并能联想类比到一元二次方程、二元一次方程等相关概念.最后的应用实质都是转化，正如笛卡尔所说“一切问题都可以转化为数学问题，一切数学问题都可以转化为代数问题，而一切代数问题又都可以转化为方程问题.因此，一旦解决了方程问题，一切问题将迎刃而解！”

5. 章头课的教学中，教师要留给学生足够的探究空间，要找出能引起学生好奇心，激发其兴趣的内容，引导学生积极开展探究活动，在活动中感悟思想方法.在探索方程的解的环节，先回顾等式的基本性质，目的是促使学生利用类比的方法探究方程解的本质，从而将学习方法正迁移.让学生初步感悟到了方程模型，同时也感知了由特殊到一般再回到特殊的研究方法.这些方法能给学生的思维注入新的活力，为今后的学习铺路搭桥.

参考文献：

［1］ 孙凯.整体建构：章头课的应然追求［J］.上海中学数学，2021（6）：5 7.