分类讨论思想解初中数学问题的不同情形应用分析

张涛

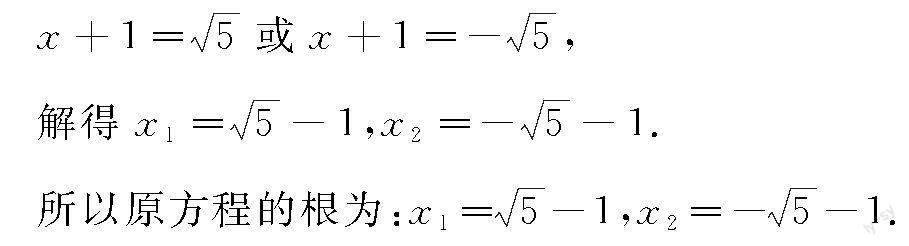
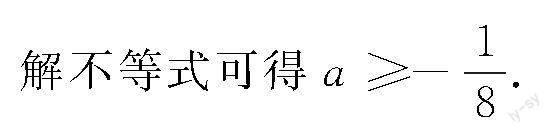
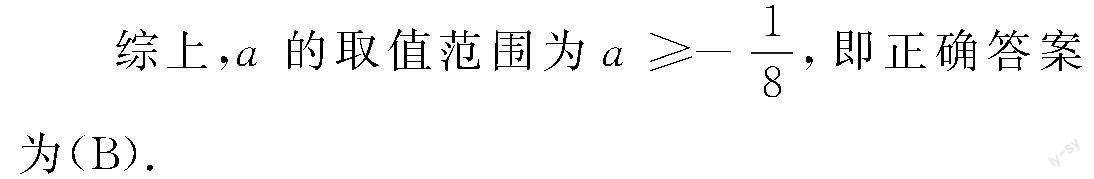
【摘要】分类讨论思想是指在一些不确定的条件下，不能用统一的思路或结论解答问题时，按照可能出现的情况分别进行讨论并解答问题的一种方法，也是解答初中数学问题的常见方法之一.本文主要对三角形问题、动点问题、方程问题的分类讨论具体应用进行具体分析，结合具体例题总结分类讨论思想的应用情形，以此帮助学生获得更高的分数，更全面地思考问题.

【关键词】初中数学；分类思想；解题研究

1 三角形问题分类讨论

三角形的边长和角度是考查的热门角度，问题通常不会给出具体的三角形图形，一些模棱两可的条件导致多種三角形存在，直接解答有可能出现漏解和误解的情况.对三角形问题分类讨论，首先根据已知条件判断三角形形状是否明确，若不确定则需要分类讨论，其次一些具有明确特征的三角形也需要分类讨论，如直角三角形未说明直角边和斜边需要分类，等腰三角形未说明明确的腰和底也同样需要分类讨论.分类讨论解题过程中，要注意三角形的分类准确不重复，才能正确解答问题.

例1 在△ABC中，∠B=25°，AD是BC边上的高，并且AD2=BD·DC，则∠BCA的度数为.

剖析 该问题没有说明△ABC的具体形状，故高AD有两种情况，分别在三角形内部和三角形外部，画出两种情况对应的图形，结合已知条件和相似三角形分析，即可得知问题所求角度.

解

①如图1，当三角形的高AD位于△ABC内部时，

由AD2=BD·DC可得△ABD∽△CAD，

因为∠B+∠BAD=90°，∠B=∠CAD，

所以∠CAD+∠BAD=∠BAC=90°，即△ABC为直角三角形，

因为∠B=25°，

所以∠BCA=90°-∠B=65°.

②如图2，当三角形的高AD位于△ABC外部时，

由AD2=BD·DC可得△ABD∽△CAD，

因为∠B=∠CAD=25°，

所以∠BCA=∠CAD+∠ADC=25°+90°=115°.

综上，∠BCA的度数为65°或115°.

2 动点问题分类讨论

初中数学中动点问题通常以几何图形作为问题背景，当动点运动到不同位置时对应的情况也有所不同，故需要分类讨论来解答问题.运用分类讨论解答动点问题时，首先应根据动点所在的不同位置进行分类，如动点位于几何图形的不同边长进行分类，其次在不同情况下分析问题涉及的函数关系，最后对所有情况进行综合从而得出答案.动点问题常常会涉及函数关系，故熟练掌握函数类型和解析式求解有助于更高效地解答这类问题.

例2 如图3，正方形ABCD的边长为3cm，动点M从点B出发以3cm/s的速度沿BC－CD－DA运动，到达点A停止运动，另一动点N同时从B点出发，以1cm/s的速度沿BA向点A运动，到达点A停止运动，设点M的运动时间为xs，△AMN的面积为ycm2，则y关于x的函数图象是（  ）

剖析 动点M与动点N都在运动，但点N运动不改变边长位置，故解题时应根据点M处于不同线段进行分类讨论，分别有点M在BC上、在CD上、在AD上三种不同情况，结合三角形面积公式表示y和x的关系得到函数表达式，即可对图象进行判断和排除，最终符合所有情况的图形即为正确答案.

解析 由题意可得BN=x，

①当0≤x≤1时，点M在BC上，

BM=3x，AN=3－x，

故（C）错误；

②当1≤x≤2时，点M在CD上，

故（D）错误；

③当2≤x≤3时，点M在AD上，

AM=9－3x，

故（B）错误.

综上，正确答案为（A）.

3 方程问题分类讨论

与方程有关的初中数学问题也同样是考查的热门题型，涉及的方程类型有一元一次、一元二次、二元一次方程，问题常常会因为存在不确定范围的参数导致方程类型不明确，需要运用分类讨论方法解题.分类讨论可以对方程的类型做出讨论，也可以对一元二次函数的实数根个数进行讨论，解答方程类问题，需要熟记一些方程的概念和实数根之间的关系表达式，结合分类讨论方法灵活运用这些知识点即可解答问题.

例3 关于x的方程a－1x2+3x－2=0有实数根，则a的取值范围为（  ）

剖析 由于方程的最高次项系数是a－1，a－1=0和a－1≠0分别对应两种不同类型的方程，分情况讨论一元一次方程和一元二次方程有实数根时对应的参数a的取值范围，即可求出正确的答案.

解析 ①当a－1≠0时，即a≠1，

由题意可得Δ=32－4a－1×－2≥0，

②当a－1=0时，即a=1，

可知一元一次方程3x－2=0有实数根，

故a=1成立.

4 结语

在解答一些数学问题时，常常会因为没有明确的定义或范围导致多种情况的出现，分类讨论思想的灵活运用是解答这些问题的关键.在三角形问题中，通常根据边长、角度两个角度进行分类，讨论不同三角形的具体情况；在动点问题中，常常根据动点所处的不同位置进行分类，讨论不同位置对应的函数关系；在方程问题中，主要根据方程类型、实数根个数进行分类，讨论对应的情况.在这些题型中应用分类讨论思想，有助于提高学生的解题效率，也能帮助学生更全面地分析问题，解决问题.