新高考下的构造函数解题方法
周思源 魏俊潮
(扬州大学数学科学学院,江苏 扬州 225002)
高考题中常见的运用构造函数法的题型有比较大小、实根个数、取值范围、极值最值与单调性问题.本文结合近几年的高考题和各地模拟题,对构造函数这一解题方法的五类常见题型和解题策略进行研究.
1 构造函数与大小关系

解析由题知f′(x)=ex-x+a,
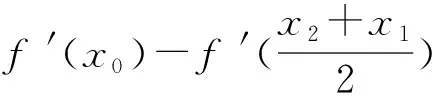
设g(x)=ex-e-x-2x,x>0,
则g′(x)=ex+e-x-2≥0.
所以g(x)在(0,+∞)单调递增,则
g(x)>g(0)=0.


2 构造函数与实根个数

(1)求实数a,b的值.
(2)证明:方程f(x)=|lnx+sinx|有且只有一个实根.
解析(1)a=1,b=-1.
令函数g(x)=lnx+sinx,x∈(0,+∞),则
当x∈[π,+∞)时,lnx>1,sinx≥-1,
所以g(x)=lnx+sinx>0.
当x∈[1,π)时,lnx≥0,sinx>0,
所以g(x)=lnx+sinx>0.


则g(x)在(0,1)单调递增.

综上所述,函数g(x)在(0,+∞)有唯一的零点x0∈(0,1),且g(x)在(0,x0)上恒小于零,在(x0,+∞)上恒大于零[1].
令函数φ(x)=f(x)-|lnx+sinx|,讨论如下:
①当x∈(0,x0)时,
φ(x)=f(x)-|lnx+sinx|
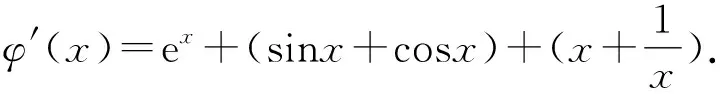


则函数φ(x)在(0,x0)单调递增.

所以函数φ(x)在(0,x0)存在唯一的零点.
则方程f(x)=|lnx+sinx|在(0,x0)上有唯一的零点.
②当x∈(x0,+∞)时,
φ(x)=f(x)-|lnx+sinx|

当x∈(0,1)时,m′(x)<0,所以m(x)在(0,1)单调递减,当x∈(1,+∞)时,m′(x)>0,所以m(x)在(1,+∞)单调递增.
则m(x)≥m(1)=1-ln1-1=0.
所以x-lnx-1≥0.

则h′(x)=ex+sinx+x-1.
因为h″(x)=ex+(cosx+1)>0,
所以h′(x)在(0,+∞)单调递增,
则h′(x)>h′(0)=0.
即h(x)在(0,+∞)单调递增.
所以h(x)>h(0)=0.
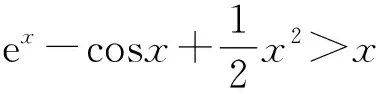

>x-lnx-sinx≥x-lnx-1≥0.
即φ(x)>0.
所以方程f(x)=|lnx+sinx|在(x0,+∞)上无零点.
综上所述,方程f(x)=|lnx+sinx|有且只有一个实根.
3 构造函数与取值范围
例3 已知函数f(x)=x2-4x+alnx,a∈R,函数f(x)的导函数为f′(x).若f′(x)有两个零点x1,x2(x1 f′(x)有两个零点x1,x2(x1 由题可得,f′(x)有两个零点x1,x2(x1 因为x1 因为0 例4已知a为正整数,若对任意x∈(0,+∞),不等式alnx≤x+1成立,则a的最大值为____. 解析由题意可知,alnx-x-1≤0对∀x∈(0,+∞)恒成立. 由题意可知,a为正整数,所以a>0. 令f′(x)=0,则x=a. 则f(x)在(0,a)单调递增,(a,+∞)单调递减. 所以需要满足f(x)max=f(a)=alna-a-1≤0. 令a=2,f(2)=2ln2-3≤0,符合题意; 令a=3,f(3)=3ln3-4≤0,符合题意; 令a=4,f(4)=4ln4-5>0,不符合题意. 所以amax=3. 例5 设函数f(x)=ex+asinx-ax2-(1+a)x.当a≤0时,讨论f(x)的单调性. 解析由题知f′(x)=ex+acosx-2ax-(1+a)=ex-1+a(cosx-2x-1), 令g(x)=cosx-2x-1, 则g′(x)=-sinx-2<0. 所以g(x)在R上单调递减,注意到g(0)=0, 当x≥0时,g(x)≤0,此时f′(x)≥0,f(x)单调递增;当x<0时,g(x)>0,此时f′(x)<0,f(x)单调递减.所以f(x)在(-∞,0)单调递减,(0,+∞)单调递增[2]. 构造函数是高考函数相关题型中的常用解题方法,本文列举了五种利用构造函数求解的函数题,针对比较大小、实根个数、取值范围、极值最值、单调性问题进行了一些研究,总结了一些利用构造函数解题的技巧,希望能为解决新高考函数问题提供一些帮助.






4 构造函数与极值最值



5 构造函数与单调性

