一道向量最值问题的多视角探究
江 浩
(江苏省沭阳如东中学,江苏 沭阳 223600)
《中国高考评价体系》指出“四翼”的高考考查要求[1],其中对综合性的考查,要求学生对同一层面的知识、能力、素养能够横向融会贯通,形成完整的知识结构、能力结构网络;对不同层面的知识、能力、素养能够纵向融会贯通.对于创新性的考查要求,指出具备良好创新思维的学生能够摆脱思维定势的束缚,善于独立思考,大胆创新.具备探索新方法、积极主动解决问题的能力.一题多解的解题教学能够很好地引导学生多角度思考问题,通过知识的多元化运用,加深知识之间的纵深联系,更加深刻地理解知识的交汇点与思路的整合点,既能拓广学生视野,也能提升学生综合运用所学知识创造性地解决问题的能力,完全符合高考评价体系中“四翼”的考查要求.本文以一道向量的最值问题为例,从不同视角探究其解决方法.
1 问题呈现

2 解法探究
解法1 因为3c=2a+b,
所以2a=3c-b.
即4a2=9c2-6b·c+b2.





点评向量的两个重要特征是大小和方向,可以通过“数”与“形”两个角度研究向量问题.解法1通过对题设两个条件的整合,消去a,更加侧重于“数”的运算.
解法2 设a与b夹角为θ,由a·b=a2,得
|b|cosθ=|a|.
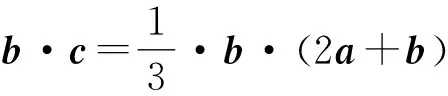

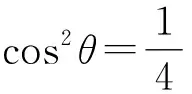


解法3 由a·b=a2,得
a·(a-b)=0.
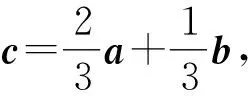

图1 构造平面几何图形

tan∠BAD=tan(∠BAC-∠DAC)




点评根据向量加法、减法、数乘与数量积运算的几何意义,研究两个条件对应的几何图形,从“形”的角度将问题直观化进行解决.
解法4 由解法3,构造如图1所示的Rt△ABC.在△ABD中,由正弦定理,知
①
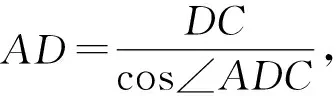
代入①式,得
sin∠BAD=2sinBcos∠ADC
=2sinBcos(∠BAD+B).
即sin∠BAD=2sinB(cos∠BADcosB-sin∠BADsinB).
所以tan∠BAD=2sinBcosB-2tan∠BADsin2B.


点评向量与解三角形有着千丝万缕的联系,向量背景下表示的几何图形为三角形,从解三角形的视角探究本题,将正弦定理与三角恒等变换等知识综合运用,能非常巧妙地解决问题.
解法5 由解法3构造的几何图形,以A为坐标原点,AC所在直线为x轴,过点A垂直于AC的直线为y轴,建立如图2所示的直角坐标系xOy.
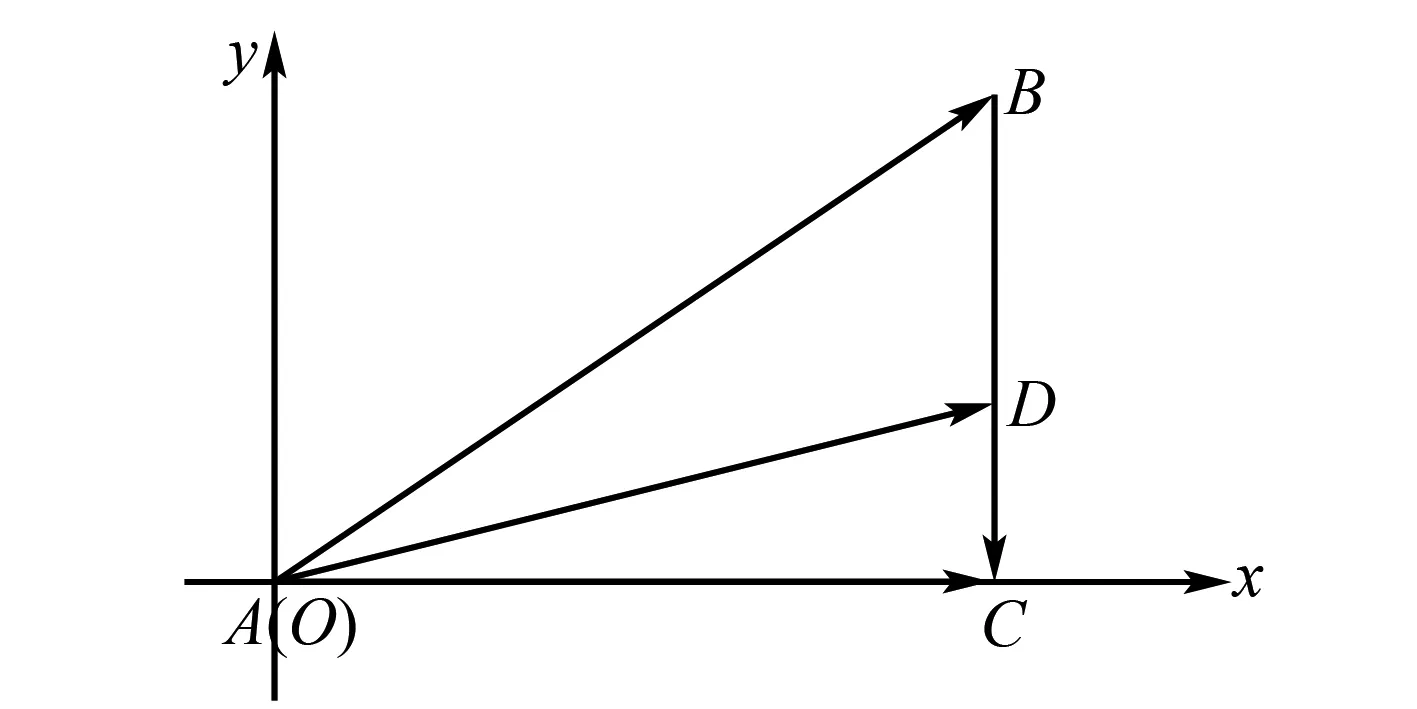
图2 建立平面直角坐标系


当且仅当tan2θ=3时取到等号.

点评向量的坐标表示是研究向量问题的重要手段[3],本题通过建立平面直角坐标系亦可解决.
解法6 由解法3构造的几何图形,以边AB中点为坐标原点,AB所在直线为x轴,边AB的垂直平分线为y轴,建立如图3所示的平面直角坐标系xOy.

图3 点C,D的轨迹
设点B坐标(r,0),其中r>0,于是由题意可知,点C的轨迹方程为x2+y2=r2,这里不妨设y>0,进一步可求得点D的轨迹方程为
可见,当AD与其相切时,∠DAB最大.



点评本题构造了一个Rt△ABC,即直角顶点C的轨迹是一个以AB为直径的圆,根据相关点法,可知点D的轨迹也为一个圆,当过点A的直线与该圆相切时,张角最大,即向量夹角余弦值最小.
教学过程中,鼓励学生从不同视角探究问题的解决方法,可以增强学生的求异思维,增进数学思维的深刻性,开拓多维创新的能力.通过数学知识与思想方法的综合运用,培养学生的数学学科核心素养.

