追求自然解法 让更多学生懂数学——以两个导数解答题为例

贾士伟

(贵州省凯里市第一中学,贵州 凯里 556000)

很多老师和学生片面追求分数,走“捷径”,乱记乱套二级结论、乱用秒杀大招,这违背了高中数学教育教学的目的,危害极大,对发展学生的数学思维毫无意义,本文呼吁解题教学要回归到自然合理上,让更多学生真正懂数学!

近几日看到某数学中等学生的笔记本上记载了“泰勒展式”“帕德逼近”等,也曾目睹一优秀学生花了大量时间啃读一本关于导数的各种“解题大招”的教辅书,但高考也未见该生考出理想成绩.乱套二级结论、乱用秒杀大招,危害极大,也违背数学教学的初衷.也有很多名校教师通过微信公众号、QQ群等分析试题,寻求题目的自然合理解法,让数学解题回归到正路上来[1].

函数与导数是高中数学的一重要内容,通常以压轴题的形式出现在各类试卷中,特别是导数解答题,由于导数解答题题型多样令很多同学望而却步.笔者看来,导数的作用基本上体现在两个方面:一是解决曲线切线问题,二是研究函数的单调性.无论是哪一种题型,用到的解题方法都是高一学的函数思想,利用数形结合研究函数的图象、函数的性质,利用函数解决方程、不等式问题,导数在其中的唯一作用是充当工具——判断函数的单调性,下面举例说明.

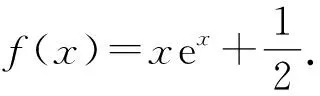
思维过程零点问题优先分离,避免繁琐的讨论,且显然0不是函数g(x)的零点.

由题知,

由g(x)=0,得

①

此时只需要作出函数h(x)图象的示意图即可,作函数图象的第一步就是研究函数的单调性,而导数是解决函数单调性的有力工具.

则p′(x)=x2(ex+1)≥0.

这里二次求导的目的是为了研究函数p(x)的单调性.

所以p(x)在R上单调递增.

所以存在x0∈(-2,-1)使得p(x0)=0.

利用零点存在性定理,研究p(x)与x轴相交的大致位置[2].

当x∈(-∞,x0)时,p(x0)<0,h′(x)>0;

当x∈(x0,0)时,p(x0)>0,h′(x)<0;

当x∈(0,+∞)时,p(x0)>0,h′(x)>0.

当x∈(-∞,0)时,

h(x)≤h(x0)

虽然无法得出x0的具体值,但可以充分利用x0满足的等量关系,x0即为隐零点[3].

当知道了函数的单调性和一些特殊函数值时,就可以得出函数h(x)的示意图.

作出函数h(x)的示意图,如图1所示,可知方程①仅有一个解.

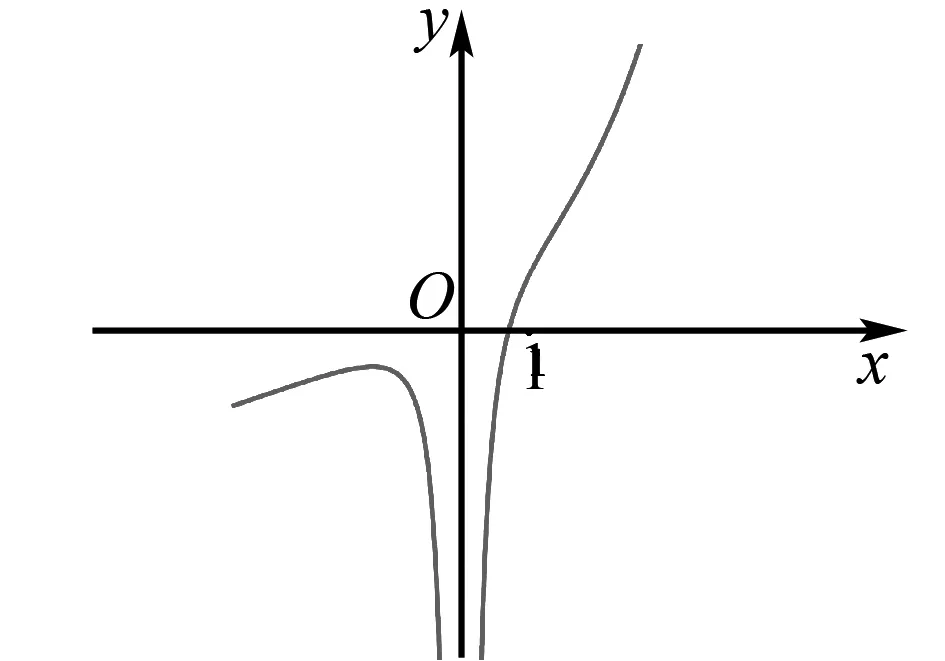
图1 函数h(x)的图象

思维过程抓住零点这一条件,建立等量关系.

由题知aex1-bx1=aex2-bx2.

由于要证的式子未知量太多,需要多元问题转化为一元问题,最后转化为函数问题,这里用分析法进行转化[4].

再将x1-x2视为整体,三元变二元,

由于解决二元变量问题最基本的思路就是固定变量,所以先视a为变量,求左边的最小值,

此时把上面的二元变量变为一元变量了.

这里是通过先化简再证明,化简原则是指幂分离,求导简单;合理换元,构造的函数尽可能简单.

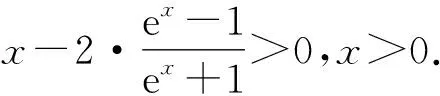
②

所以函数g(x)在(0,+∞)上单调单增.

所以g(x)>g(0)=0,②式得证.

通过高中数学的教育教学应当使学生掌握数学的基础知识、基本技能、基本思想;使学生表达清晰,思考有条理;使学生会用数学的思考方式解决问题、认识世界.花大量时间死记二级结论,解题时不加思考乱套二级结论,偏离学习主题,用高等数学知识“秒杀”初等数学试题,这些行为对发展学生的数学思维毫无用处[5].

从近几年教育部考试中心的高考试题评析中可以知道:现在的高考试题改变了相对固有的试题形式,增强了试题的开放性,减少死记硬背和“机械刷题”.“以考促改”,高考的变革促使教师的解题教学应该回到“正常”状态,跳出“模型”“大招”,在解题中应该追求自然合理的解法,教学生解决问题的基本思想和方法,让更多学生更好地理解数学的思想方法.“授人鱼不如授之以渔”,只要学生具备了自主思考能力,才会用所学知识解决“万变不离其宗”的各种问题.