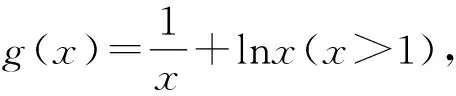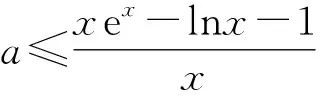用“同构思想”解决函数问题的策略研究
李 波
(四川省南充高级中学,四川 南充 637901)
通过分析2020-2022年高考真题,发现在近三年的高考中频繁出现通过构造函数解不等式题目(见表1).文[1]中研究了同构变形在函数问题中的3个基本应用,文[2]中说明了构造同构函数可以简化哪些基本结构,常见的函数结构有哪些?文[3]阐述了通过同构变换实现变量分离,解决含参问题的基本优点与策略.通过研究该类题型的命题特点和解题方法,归纳出同构函数的基本策略.

表1 真题分布
1 观察规律,直接构造

A.a C.c 解析构造函数f(x)=(2-x)ex,则f′(x)=(1-x)ex.易知f(x)在(-∞,1)上单调递增,在(1,+∞)上单调递减. 故选A. 将变量x1,x2归类整理为(x1+1)f(x1)-m(x1+1)2<(x2+1)f(x2)-m(x2+1)2. 由t1>t2,知g(t)在(1,+∞)上单调递减. 评析已知对∀x1,x2∈D,x1 即g(lnx1)=g(x2). 又k<0,所以lnx1,x2∈(-∞,0),根据g(lnx1)=g(x2),可得lnx1=x2. 令F(x)=x2ex(x<0),则F′(x)=x(x+2)ex. 例4 (2022年新高考Ⅰ卷22题)已知函数f(x)=ex-ax和g(x)=ax-lnx有相同的最小值. (1)求a; (2)证明:存在直线y=b,其与两条曲线y=f(x)和y=g(x)共有三个不同的交点,并且从左到右的三个交点的横坐标成等差数列. 解析(1)a=1,过程略. (2)由(1)知,f(x)=ex-x在(-∞,0]单调递减,在(0,+∞)单调递增. g(x)=x-lnx在(0,1]单调递减,在(1,+∞)单调递增,图象如图1所示. 图1 2022年新高考Ⅰ卷22题 若直线y=b与两条曲线y=f(x)和y=g(x)共有三个不同的交点,设三个交点的横坐标分别为x1,x2,x3,且x1<0 由①②,知ex1-x1=x2-lnx2=elnx2-lnx2. 又f(x)=ex-x在(-∞,0)上单调递减,所以x1=lnx2. 由②③,知 ex2-x2=x3-lnx3=elnx3-lnx3. 又f(x)=ex-x在(0,+∞)上单调递增,x2=lnx3,所以x3=ex2. 由②可得,2x2=lnx2+ex2=x1+x3. 所以三个不同交点的横坐标成等差数列. 评析针对和差型:ex1-x1=x2-lnx2,研究方案有两种:一是以ex-x为基准,变形ex1-x1=elnx2-lnx2;二是以x-lnx为基准,变形ex1-lnex1=x2-lnx2.再构造对应的同构函数,结合函数单调性,利用对应地位相等解答. A.a C.a 即a (1)讨论函数f(x)的单调性; (2)已知λ>0,若存在x∈(1,+∞),不等式λx2-λx≥(eλx-1)lnx成立,求实数λ的取值范围. 解析(1)f(x)在(0,1),(1,+∞)单调递减. (2)由λx2-λx≥(eλx-1)lnx,知 λx(x-1)≥(eλx-1)lnx. 即f(x)≤f(eλx). 由λ>0,x∈(1,+∞),知eλx>1. 根据f(x)在(1,+∞)单调递减,可得x≥eλx. (1)若f(x)≥0,求a的取值范围; (2)证明:若f(x)的两个零点x1,x2,则x1x2<1. 解析(1) 由题知,f(x)的定义域为(0,+∞). 易知h(x)在(0,1)单调递减,在[1,+∞)单调递增.所以当x=1时,h(x)有最小值1. 再令g(x)=ex+x(x≥1), 易知g(x)=ex+x在[1,+∞)单调递增. 所以当x=1时,g(x)有最小值e+1, 所以a≤g[h(x)]min=e+1. 例8 对于任意实数x>0,不等式2ae2x-lnx+lna≥0恒成立,则a的取值范围是____. 解析由2ae2x-lnx+lna≥0,知 e2x+ln2a-lnx+lna≥0. 不等式两边同时加2x+ln2,则 e2x+ln2a-lnx+2x+ln2a≥2x+ln2. 整理,得e2x+ln2a+2x+ln2a≥2x+ln2x. 令f(x)=ex+x,则f(2x+ln2a)≥f(ln2x). 易知2x+ln2a≥ln2x. 即ln2a≥ln2x-2x恒成立. 评析确定好内函数去构造外函数,积型:aea≤blnb,研究方案有三种:一是保留左边aea≤lnbelnb,构造函数f(x)=xex;二是保留右边ealnea≤blnb,构造f(x)=xlnx;三是两边同时取对数a+lna≤lnb+ln(lnb),构造函数f(x)=x+lnx. 在解决函数的综合问题时,若尝试将不等式H(x)≥0变形为F[f(x)]≥F[g(x)],利用函数的单调性转化为解f(x)≥g(x)或f(x)≤g(x),形式F[f(x)]≥F[g(x)]需要自己去构造,基本的思路为: 即x09x0=-t9-t. 令h(x)=x9x,易知h(x)在(0,+∞)单调递增. 由h(x0)=h(-t),知x0=-t. 解得9x0(x0-1)=1.故选B. 解析由题知a>0,则 不等式两边同时取自然对数,则x-lna≥lnt. 所以当x=1时,h(x)有最小值e+1. 即a≤e+1. 评析有些式子不能启发我们同构,不易向同构的方向变形,可以尝试换元法,通过换元的过程来启发我们新的解题思路. 两边同时取自然对数,得alnx=xlna. 图2 函数g(x)图象 例12 设k>0,若存在正实数x,使得不等式log4x-k·2kx-1≥0成立,则k的最大值为 ( ). 解析由log4x-k·2kx-1≥0,知 令t=2k,t>1,则logtx≥tx. 则xlnx≥exlnt·(xlnt). 由t>1知,xlnx≥exlnt·(xlnt)>0. 所以x>1,xlnt>1. 由f(x)≥f(exlnt),知x≥exlnt. 即存在正实数x,满足lnx≥xlnt. 不等式两边同时加x-1,得 易知g(x)在(1,+∞)单调递增. 因为ex-1>x,所以g(ex-1)>g(x)恒成立. 由x>1知,a≥1. 例14 已知函数f(x)=lnx+ax+1(其中a∈R).对于任意x>0,不等式f(x)≤xex恒成立,求实数a的取值范围 评析对解决某些指对混合不等式问题,往往要结合切线放缩,进行局部同构,这样可以大大降低这类问题的难度,但要注意取等号的条件以及常见变形等[3]. 同构法在近几年的高考中频繁出现,命题者立足教材基本知识、基本技能,把等式或不等式变形为两个结构(形式)一样的函数,利用函数的单调性比较大小、解决恒成立、求参数范围等问题,既考查了学生的核心素养,又培养了学生的创新能力,体现考试的选拔功能,落实《深化新时代教育评价改革总体方案》的要求,改变相对固化的试题形式,增强试题的灵活性,减少死记硬背和机械刷题,让试题变得更加开放与综合.

2 双元变量,归类整理








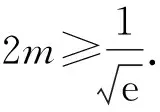
3 方程思想,地位对等

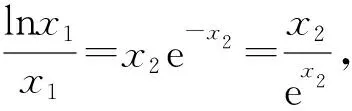
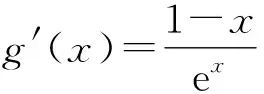



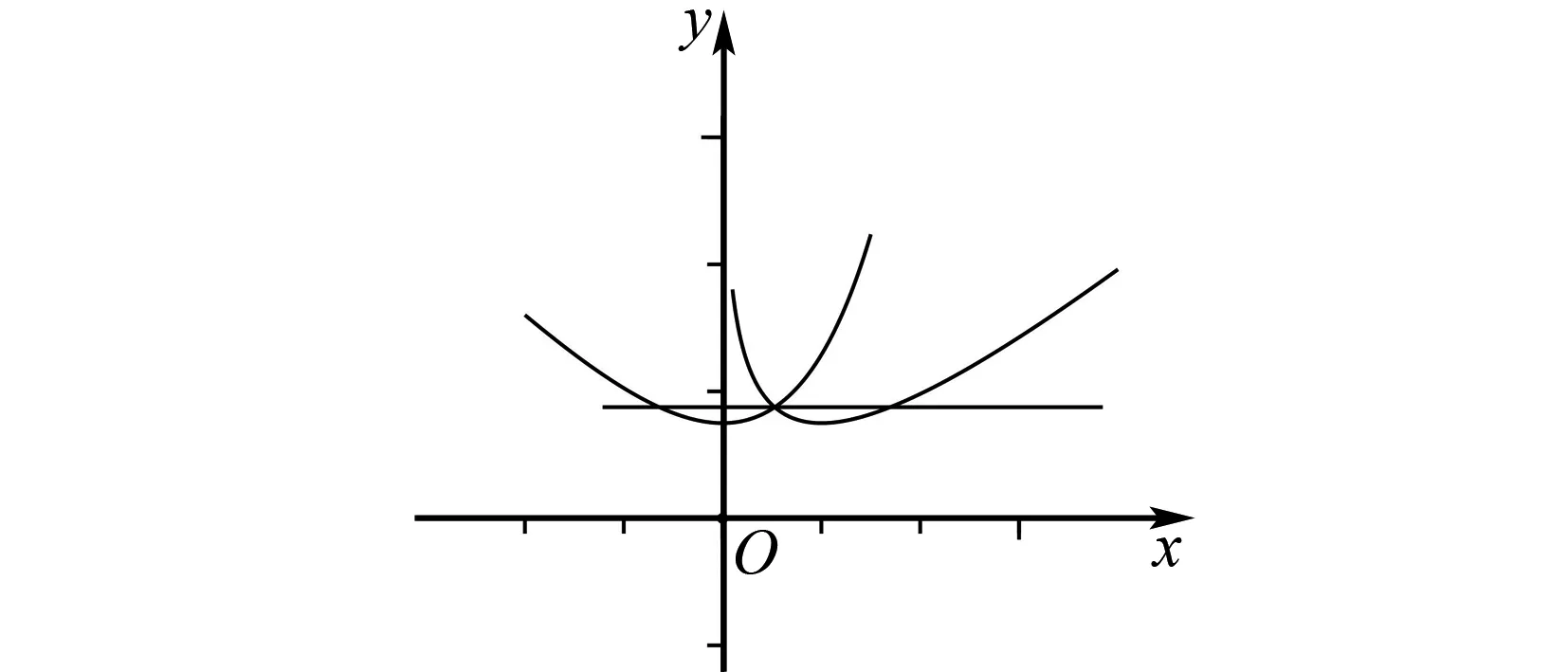
4 确定外函数,拼凑内函数

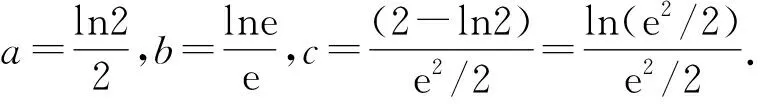
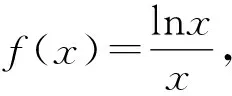



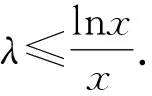


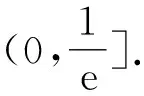

5 确定内函数,构造外函数
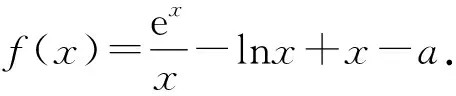

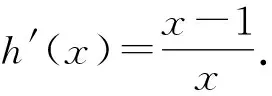



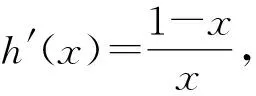


6 局部换元,简化结构
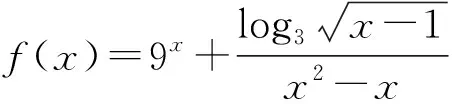

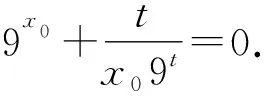










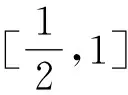
7 利用性质,整理变形



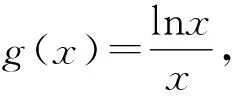

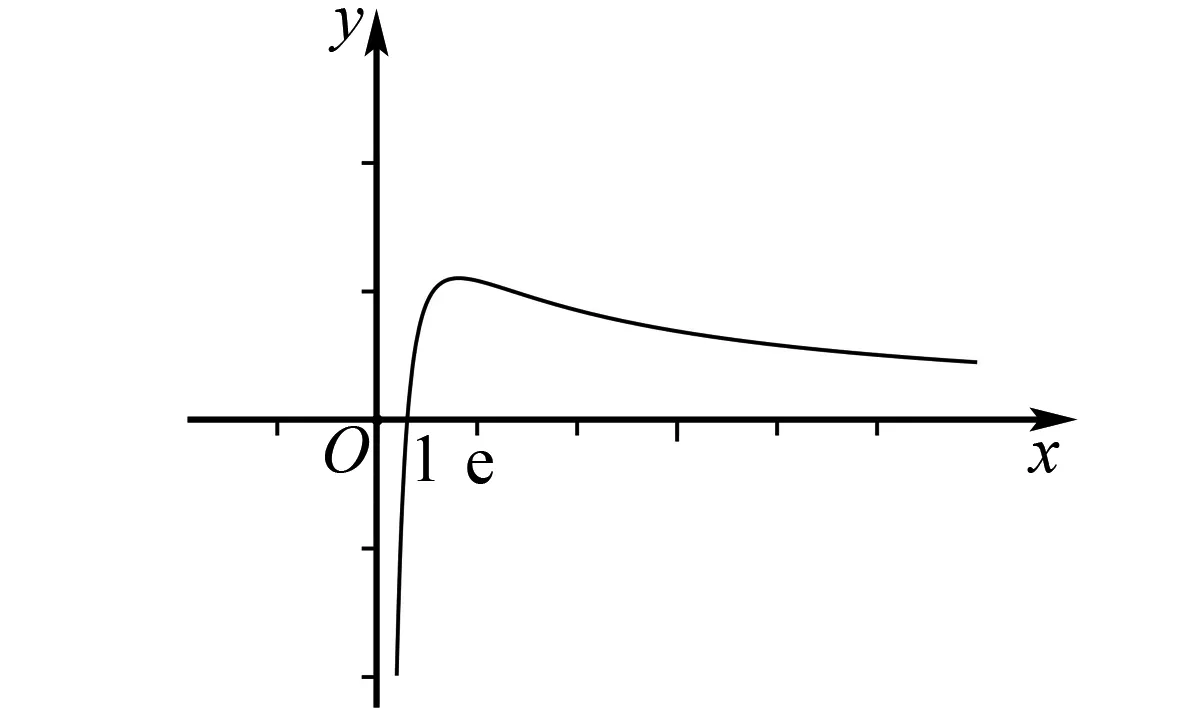
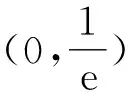


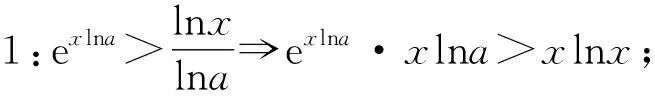
8 同构路上,亦可放缩