求解空间几何体体积问题的基本策略
侯有岐
(陕西省汉中市四〇五学校,陕西 汉中 723312)
空间几何体的体积问题是高考的必考内容,主要以选填题或解答题(文科)的形式出现,难度中等,侧重考查学生的空间想象、数形结合、转化与化归以及数学运算求解等能力.关于空间几何体的体积问题,依据题设的特殊性,常用的解题方法有:公式法、等体积变换法、分割法、补形法、函数法和向量法等,有时还可用平移法、相似比法、祖暅原理法等求解,凸显 “化非规则为规则,化不可求为可求,或化不易求为易求”的整体思维的具体应用. 本文以近几年高考试题和模拟试题为例归类解析,以期帮助学生迅速提升解题能力.
1 公式法
例1 (2022年全国甲卷(文、理)·4) 如图1,网格纸上绘制的是一个多面体的三视图,网格小正方形的边长为1,则该多面体的体积为( ).

图1 多面体三视图
A.1.8 B.12 C.16 D.20
分析由三视图还原成原几何体,可知该几何体为直四棱柱,直接代入棱柱的体积公式即可得答案.
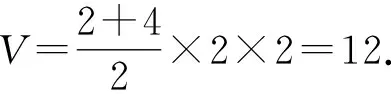
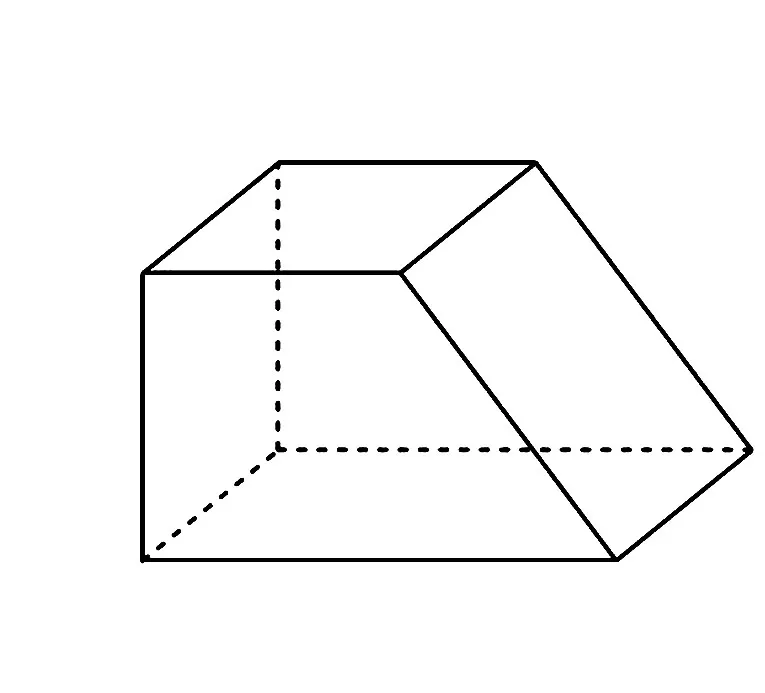
图2 三视图还原几何体图
点评本题考查由三视图求体积,关键是由三视图正确还原原几何体,是中档题.本题考查了转化与化归和基本分析求解能力.
公式法也叫直接法,一般适用于几何体形状整齐,有较明显的垂直关系且长度已知的题型.用公式法求几何体的体积要先确定高和底面积,对于高的确定一定要先证明该线垂直于底面,不可以凭感觉判定.另外,还要记住柱、锥、台、球等常用几何体体积公式.

分析设母线长为l,甲圆锥底面圆半径为r1,乙圆锥底面圆半径为r2,根据圆锥的侧面积公式可得r1=2r2,结合圆心角之和可将r1,r2分别用l表示,利用勾股定理分别求出两圆锥的高,再根据圆锥的体积公式即可得解.

所以r1=2r2.



故选C.


变式(2020年江苏卷·9)如图3,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm,高为2 cm,内孔半径为0.5 cm,则此六角螺帽毛坯的体积是____cm3.

图3 2020年江苏卷9题图

2 等体积变换法


图4 2022年新高考Ⅰ卷19题图
分析由等体积变换法运算即可得解.



点评点到平面的距离的求解问题要么直接求解,要么设出来用等体积法求解.等体积变换法(换顶点)大多用于与锥体体积有关的问题中,尤其是三棱锥,这是因为三棱锥的任何一个面都可以作为底面.转换原则是换底高易求或底面放在已知几何体的某一面上.
变式(2019年全国Ⅰ卷文·19)如图5,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.求点C到平面C1DE的距离.

图5 2019年全国Ⅰ卷文19题图

因为棱柱为直棱柱,所以DE⊥平面BCC1B1.
所以DE⊥EC1.



3 分割法
例4 (2018年江苏卷·10)如图6所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为____.

图6 2018年江苏卷10题图
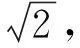
点评解决本类题目的关键是准确理解几何体的结构特征,可以判断所求几何体可以分割为两个全等四棱锥.割补法求几何体的体积是比较常规的方法,比如多面体切割成锥体特别是三棱锥,需要有整体与局部结构意识.
变式(2019年Ⅲ卷文理·16)学生到工厂劳动实践,利用3D打印技术制作模型.如图7,该模型为长方体ABCD-A1B1C1D1挖去四棱锥O-EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=6 cm,AA1=4 cm,3D打印所用原料密度为0.9 g/cm3,不考虑打印损耗,制作该模型所需原料的质量为____g.

图7 2019年Ⅲ卷16题
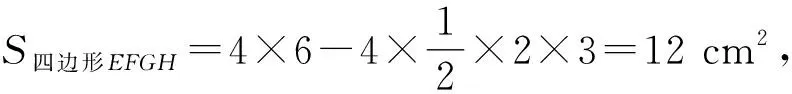
又长方体ABCD-A1B1C1D1的体积为V2=4×6×6=144 cm3,所以该模型体积为V=V2-V1=144-12=132 cm2,其质量为0.9×132=118.8 g.
4 补形法
例5(2019年Ⅰ卷理·12)三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为( ).
分析由题意画出图形(如图8),证明三棱锥P-ABC为正三棱锥,且三条侧棱两两互相垂直,再由补形法求外接球球O的体积.

图8 2019年Ⅰ卷理12题
解法因为PA=PB=PC,△ABC是边长为2的等边三角形,所以P-ABC为正三棱锥.
所以PB⊥AC.
又E,F分别为PA,AB中点,所以EF∥PB.
所以EF⊥AC.
又CE∩AC=C,
所以EF⊥平面PAC,PB⊥平面PAC.
所以∠APB=90°.


点评本题考查多面体外接球体积的求法,考查空间想象能力与思维能力,考查计算能力,是中档题.可通过线面垂直定理得到三棱两两互相垂直的关系,得到侧棱长,利用补全图形法解决问题[1].
一般地,若三棱锥的三条侧棱互相垂直且相等,则此三棱锥可以补形为一个正方体;若三棱锥的三条侧棱互相垂直但不相等,则此三棱锥可以补形为一个长方体,且长方体的体对角线长就是该三棱锥的外接球的直径.



图9 2017届贵州省遵义模拟题图

点评割补本来属于同一个思想,分割是向内视角,补全是向外视角,但是大多数时候学生都是分割处理,向外的视角不易想到,为了强化此种意识,将割补分为两类进行归纳分析.比如将三棱柱补成平行六面体,三棱锥补成四棱锥或三棱柱或平行六面体,将圆锥放在圆柱体中,等等.此题就是把三棱锥补全到正方体中,从而利用整体全局意识解决问题.
5 函数法

分析设正四棱锥的高为h,由球的截面性质列方程求出正四棱锥的底面边长与高的关系,由此确定正四棱锥体积的取值范围.
解析因为球的体积为36π,所以球的半径R=3,设正四棱锥的底面边长为2a,高为h,则
l2=2a2+h2,32=2a2+(3-h)2.
所以6h=l2,2a2=l2-h2.



点评立体几何中求体积的最值(或范围)问题,利用函数思想,特别是利用导函数或均值不等式求取最值,是一次精彩的综合交汇,首先要理清数量关系,然后将图形和文字转化至数学语言,用数学建立函数模型,最后通过函数求最值的方法解决问题.
变式(2017年全国Ⅰ卷理·16)如图10,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边△ABC的中心为O.D,E,F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D,E,F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为____.

图10 2017年全国Ⅰ卷理16题图
解析如图11,连接DO交BC于点G,设D,E,F重合于点S,正三角形的边长为x(x>0),则





6 向量法
例7(2021年新高考Ⅰ卷·20)如图12,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.若△OCD是边长为1的等边三角形,点E在棱AD上,DE=2EA,且二面角E-BC-D的大小为45°,求三棱锥A-BCD的体积.

图12 2021年新高考Ⅰ卷20题
分析建立合适的空间直角坐标系,设A(0,0,m),利用待定系数法求出平面的法向量,由向量的夹角公式求出m的值,然后利用锥体的体积公式求解即可.


图13 坐标法图




解得m=1.



解法2 (传统几何法)作出二面角的平面角,如图14所示,作EG⊥BD,垂足为点G.作GF⊥BC,垂足为点F,连接EF,则OA∥EG.

图14 传统几何法图
因为OA⊥平面BCD,所以EG⊥平面BCD,∠EFG为二面角E-BC-D的平面角.
因为∠EFG=45°,所以EG=FG.
由已知得OB=OD=1,故OB=OC=1.



点评解法1通过建立空间直角坐标系是理科生解决立体几何的常见方法,即几何问题代数化,体现向量的实用价值.解法2找到二面角的平面角,然后对几何体的几何特征进行研究,在本题中属于比较好的方法.
变式(2021年乙卷数学文科18题)已知四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,M为BC的中点,且PB⊥AM.
(1)证明:平面PAM⊥平面PBD(解析略);
(2)若PD=DC=1,求四棱锥P-ABCD的体积.



故四棱锥P-ABCD的体积
解法2 (平面直角坐标系法)由(1)知AM⊥DB,所以kAM·kBD=-1.
建立如图15所示的平面直角坐标系,设BC=2a(a>0),因为DC=1,所以A(0,0),B(1,0),D(0,2a),M(1,a).

图15 平面直角坐标系图


下同解法1.
解法3 (空间直角坐标系法)以D为坐标原点建立如图4所示的空间直角坐标系D-xyz,设|DA|=t,所以D(0,0,0),C(0,1,0),P(0,0,1),A(t,0,0),B(t,1,0).




又PD⊥底面ABCD,AM在平面ABCD内,
因此PD⊥AM.





点评本题破题关键是求出矩形ABCD的边长BC,解法1利用相似三角形求出矩形ABCD的边长BC,从而求得该四棱锥的体积;解法2建立平面直角坐标系,利用直线垂直的条件得到矩形ABCD的边长BC,从而求得该四棱锥的体积;解法3直接利用空间直角坐标系和空间向量的垂直的坐标运算求得矩形的边长;解法4利用空间向量转化求得矩形的边长.所有解法中解法3最为简捷,可见空间向量法在解决立体几何问题中的优越性.
总之,立体几何中有关体积问题,高考考查的形式已经由原来的简单套用公式渐变为与三视图及柱、锥、球的接、切问题相结合.而求锥体体积的常用方法是等价转化法,转化原则是其高易求,底面放在已知几何体的某一面上;求规则几何体体积的常用方法是公式法、整体法等;求不规则几何体的体积常用分割或补形的思想,将不规则几何体转化为规则几何体以便于求解,常见方法有等体积法、割补法、函数法、向量法等.

