一道求直线过定点问题的四种解决策略
2023-10-11 01:11王弟成
数理化解题研究 2023年25期
王弟成
(江苏省苏州实验中学,江苏 苏州 222006)
求直线过定点问题是解析几何中的常见题型之一,也是高考重点考查的内容,因此解决它需要综合运用解析几何知识,同时还要注意解题策略的运用.

(1)求椭圆C的标准方程;
(2)斜率不为0的直线l与C交于M,N两点,若直线BM的斜率是直线AN斜率的两倍,证明:直线l经过定点,并求出其定点坐标.

1 设且求,选择斜率k表示出相应直线方程
策略1 从已知条件出发,选择直线AN的斜率k表示点M,N的坐标,进而表示出直线l的方程,从直线方程中挖掘出定点.



(3+16k2)x2-64k2x+64k2-12=0.

所以直线l的方程为
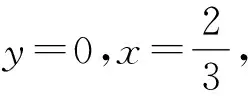

2 先猜后证,减少运算
策略2先利用特殊情况猜想出直线所过的定点,再利用斜率或向量证明三点共线,从而得到直线恒过定点.
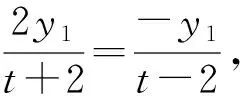



3 设而不求,整体处理
策略3 上面解法的主要困难在于得到的直线l方程复杂,不易观察定点.此时还可以考虑直接设出直线l方程,根据条件找到方程中相关参数的关系,此时再确定定点就很容易.










(t+2)y1=my1y2+2(t-2)y2.

即(3t-2)(t+2)y1=(t-2)(3t-2)y2.
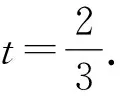
4 用性质换点,寻求对称性

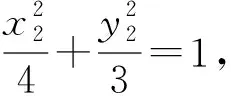




上面的每一种解决方法都有其优点,解决问题时需要根据具体情境,明确方向,识别模型,选择模型,确定方法.高三解题理应策略优先,只有对各种情况分析透彻,把握本质,才能在考试中选择合适的方法解决问题.
猜你喜欢
中学生数理化(高中版.高考数学)(2022年4期)2022-05-25
现代苏州(2022年6期)2022-04-13
今日农业(2021年21期)2021-11-26
新世纪智能(教师)(2021年2期)2021-11-05
教育周报·教育论坛(2021年21期)2021-04-14
物理之友(2020年12期)2020-07-16
地理空间信息(2017年2期)2017-03-02
福建中学数学(2016年7期)2016-12-03
光学精密工程(2016年1期)2016-11-07
电测与仪表(2016年6期)2016-04-11

