数形结合思想在初中数学解题中的应用

香钦源

【摘  要】  数形结合在数学解体中应用范围广，解决题型多，是解决高考题型的常用解体方法.

【关键词】  初中数学;数形结合;应用解题

1  数形结合在函数问题中的应用

例1  若定义在区间内的函数满足，则a的取值范围是（   ）

（A）.   （B）.    （C）.   （D）.

分析  由在定义区间内，

可知函数在内的图象位于轴上方，

且时，（如图1所示），

所以底数应满足，得，选（A）.

例2  已知函数的图象如图2所示，则（   ）

（A）.  （B）.    （C）.   （D）.

分析  依据图象，可得函数的图象经过了点，，，，

因此有

解得，

所以．

显然由或，

即可解得选（A）．

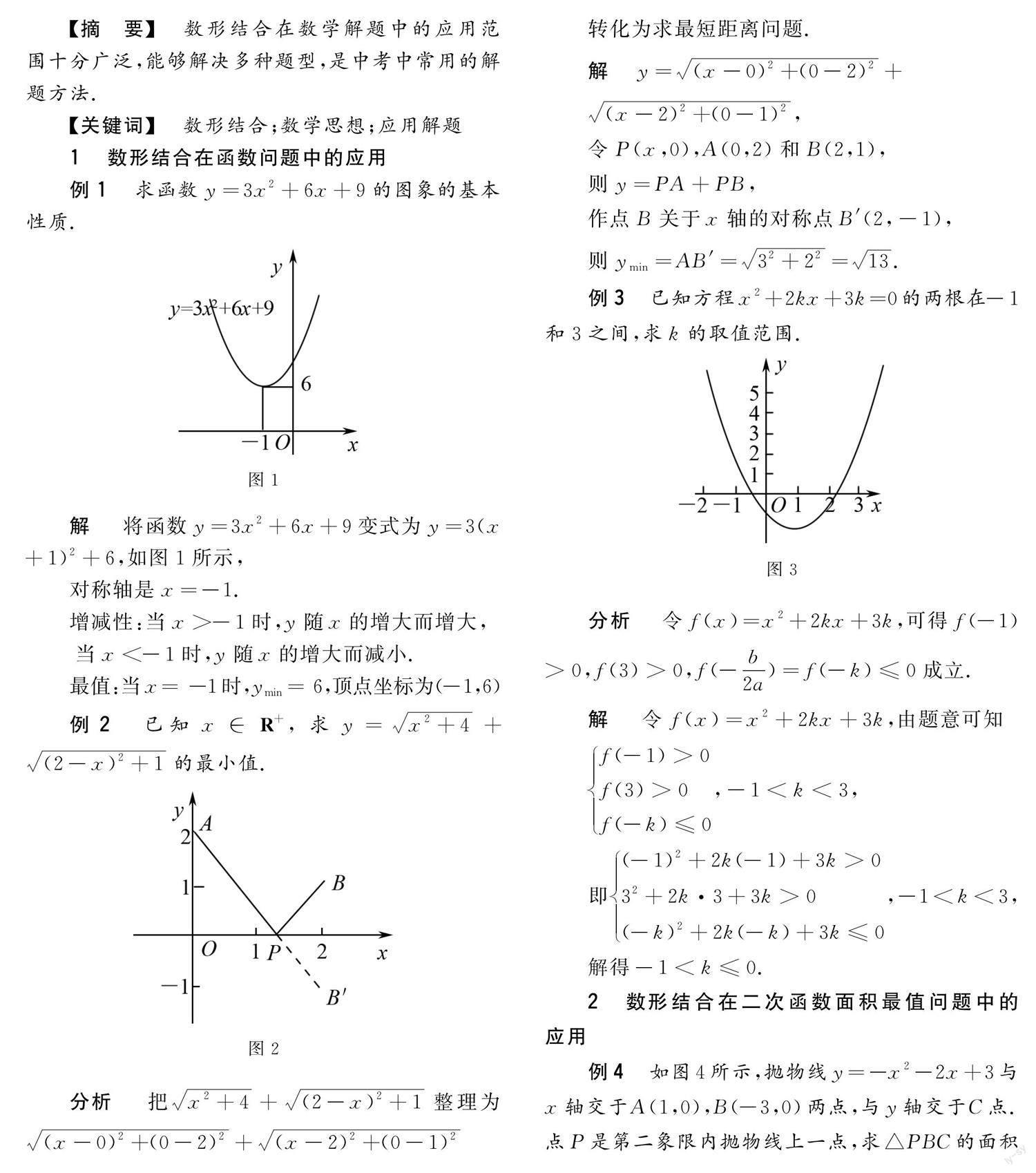
例3  求函数的图像的基本性质

解  将函数变式，如图3所示.

对称轴是，

增减性：，随的增大而增大，

，随的增大而减小，

最值：当时，，顶点坐标，

2  数形结合在方程和不等式中的应用

2.1  数形结合在方程中的应用

例4  求方程解的个数.

解  函数与的图象如图4，

即方程的解的个数，

即函数，的图象的交点个数只有1个解.

2.2  数形结合在不等式中的应用

例5  解不等式 ，其中.

方法一：∵，依據题意得．

∴，

∴，

结合可知．

据此，两边平方得，

∴，

按照三类，，讨论取解即可．

方法二：已给不等式和得，

即，

所以，当时，所给不等式的解集为；

当时，所给不等式的解集为．

方法三：作函数和的图象，如图5所示．

得出：当时，不等式的解集为；

当时，所给不等式的解集为．

2.3  数形结合在三角函数中的应用

例6  设函数．

（1）证明，其中为整数；

（2）设为的一个极值点，证明 ．

证明  （1）由函数的定义，对任意整数，

有，

∴．

（2）函数在定义域R上可导，.

令， 得 ．

若，则，

这与矛盾，所以．

当时，．

由于函数的图象和函数的图象知，

有解，的极值点一定满足.

当时，

.

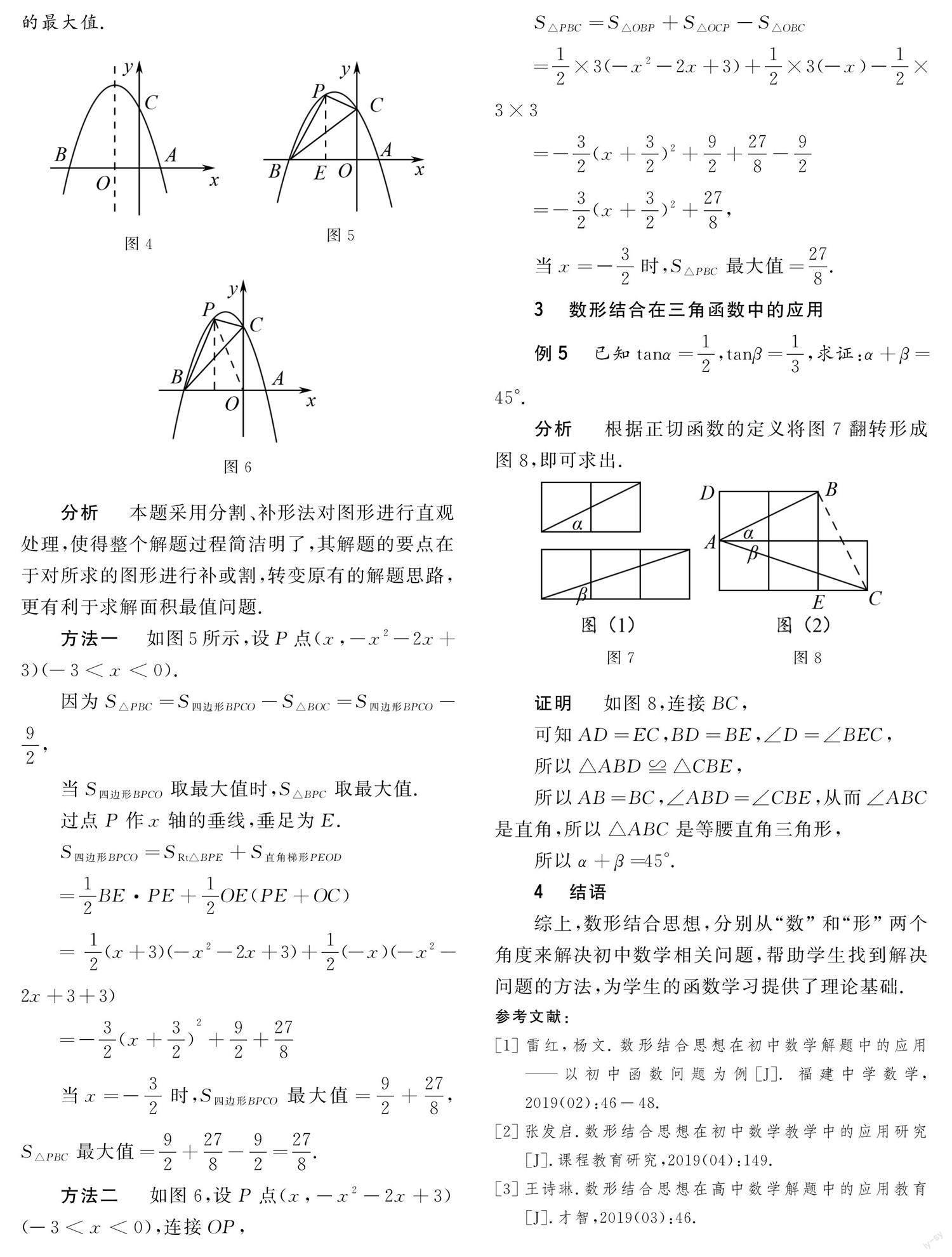
2.4  数形结合在最值问题中的应用

例7  已知，，且.求函数 的最值.

解   ∵ ∴.

∴.

又∵，

∴.

∴梯形顶点坐标为，，，

设，

则，是经过点且斜率为的直线在轴上的截距.

观察平行线簇，易知截距取最大值，截距为最小 .

∴   .

2.5  数形结合在几何中的应用

例8  四棱锥中，底面为矩形，

侧面底面，，，．

（1）证明：；

（2）设与平面所成的角为，求二面角的大小．

①证明  作，垂足为，连接，

由题设知，底面，且为中点，

由知，∽，

从而，于是，

由三垂线定理知，.

②由题意，，所以⊥侧面，

又侧面，所以侧面⊥侧面.

作，垂足为，连接，则平面，

故为与平面所成的角，，

由，得，

又，因而，所以为等边三角形，

作，垂足为，连接.

由（I）知，，又，

故平面，

，∴是二面角的平面角.

所以二面角为

参考文献：

[1]雷红，杨文.数形结合思想在初中数学解题中的应用——以初中函数问题为例[J].福建中学数学，2019（02）：46-48.

[2]张发启.数形结合思想在初中数学教学中的应用研究[J].课程教育研究，2019（04）：149.

[3]王诗琳.数形结合思想在高中数学解题中的应用教育[J].才智，2019（03）：46.

[4]罗惠庭.数形结合思想在初中数学解题教学中的渗透策略[J].中学数学研究（华南师范大学版），2018（20）：17-19.