新工科背景下的“高等数学”课程建设探究

陈翠玲 罗荔龄

［摘 要］ 从传统“高等数学”课程教学中存在的问题、新工科背景下“高等数学”课程与专业课程交叉与融合的重要性、建设以问题驱动和专业导向为着力点的“高等数学”新课程的意义、如何进行“高等数学”课程建设及“高等数学”课程建设中需要改变的方向五个方面进行阐述，对新工科背景下建设“高等数学”课程進行较深入的探究。其中，以函数的最大值最小值内容为例，从导入新课、讲授新知、巩固新知三个环节说明如何通过问题驱动和专业导向进行“高等数学”课程建设，以满足新工科背景下对多元化、创新型人才的培养需求。

［关键词］ 新工科；高等数学；课程建设；问题驱动；专业导向

［基金项目］ 2022年度广西壮族自治区高等教育本科教学改革工程项目“‘问题驱动+‘专业导向：新工科背景下高等数学课程建设的研究与实践”（2022JGA125）；2022年度广西壮族自治区高等教育本科教学改革工程项目“‘三位一体提效数学师范生实践教学能力的教学改革与实践”（2022JGA130）

［作者简介］ 陈翠玲（1978—），女，江西彭泽人，硕士，广西师范大学数学与统计学院副教授，主要从事优化理论与算法研究；罗荔龄（1979—），女，广西临桂人，博士，广西师范大学数学与统计学院讲师，主要从事数学教育研究。

［中图分类号］ G642.0［文献标识码］ A ［文章编号］ 1674-9324（2023）25-0071-04 ［收稿日期］ 2022-09-09

一、传统“高等数学”课程教学中存在的问题

长期以来，受传统教学模式和教师对课程传统认知的影响，“高等数学”课程教学大多面临着以下几个问题。

（一）教学模式单一

传统的“高等数学”课程主要采用教师全程教、学生被动学的教学模式，课堂内的时间以教师讲授为主。但通常教师只是照搬教材内容进行教学，完成教学任务时只注重知识的输出，而不关注学生对知识的感兴趣程度。学生只能被动地接受知识，无法发挥学习的主动性。

（二）教学观念陈旧

传统的“高等数学”课程教学中，教师通常仅以高等数学教材为参照，很少参阅专业课程的教材，导致对学生的专业了解程度不高，对高等数学知识的应用价值了解不够，只注重讲授高等数学知识，而不注重讲授知识的产生来源，忽视了知识的产生背景和应用价值，忽略了在教学中凸显高等数学知识与专业课程知识的联系。在这种观念下，学生被动地学习了高等数学知识，但不明白为何要学、如何应用。

（三）教学内容重理论轻应用

现有“高等数学”教学内容仅根据数学自身的学科特点进行设置，只能体现高等数学知识的理论性、严谨性和逻辑性，忽略了高等数学知识与专业课程知识、其他学科知识的联系，不能根据学生的专业有针对性地将高等数学知识与专业课程知识相联系，忽略了高等数学知识的应用，导致“高等数学”课程的教学内容与专业知识严重脱节。

（四）教材对于专业课程的针对性不强

高校现有“高等数学”课程大多采用普通本科通用的教材，所有工科专业学生使用的高等数学教材内容几乎相同，没有基于不同专业的发展需求进行内容设置，无法体现专业特色。这些教材不能直接体现高等数学知识与专业课程知识之间的联系，不能使学生感受到高等数学知识对于专业学习的重要性，从而导致学生对于学习“高等数学”课程产生懈怠情绪，主动性不高，学习兴趣不足，从而影响了教学效果。

二、新工科背景下“高等数学”课程与专业课程交叉融合的重要性

新工科是国家为应对科技革命和产业变革、支持“中国制造2025”等国家战略而提出的工程教育改革战略［1］，其内涵是以立德树人为引领，以应对变化、塑造未来为建设理念，以继承与创新、交叉与融合、协调与共享为主要途径，培养未来多元化、创新型卓越工程人才［2］。“高等数学”作为工科专业的基础理论课之一，是所有工科学生的必修课程，不仅是学生学习专业知识和专业技能的必备基础，更是其提高创新能力必须具备的基本素养。国家和社会的发展都需要科技，科技的发展需要知识。学生只有学好“高等数学”课程，才可能学好专业课程，更好地掌握科技知识。高等数学知识对于学生学习专业课程知识、掌握未来科技的重要性显而易见。因此，将高等数学知识与专业课程知识进行交叉融合，是满足新工科背景下人才发展需求的必然之举。

三、建设以问题驱动和专业导向的“高等数学”课程的意义

在新工科背景下，“高等数学”课程教学不仅要求教师传授知识，还需要教师结合专业课程知识体现高等数学知识的应用性，通过将高等数学知识与专业课程知识结合的方法，改进传统教学中过于片面地强调高等数学知识的不足，提高学生应用知识的能力，体现高等数学知识的应用价值［3］。只有注重学习和应用的双重价值，注重学生知识和能力的全面提升，才能培养出多元化、创新型的卓越工程人才。

问题驱动教学模式（Problem-based Learning，PBL），是以问题为引领、以解决问题为导向、以享受探究问题解决之道的过程为教学内容展开的教学方法［4］，由英国教育家博雷泊在20世纪80年代提出［5］。这种教学模式的核心是以学生为主体，以问题为起点，围绕寻求问题解决方案的核心规划展开学习内容。其目的是在问题求解的探究发现中，通过师生互动提升学生在教学过程中的参与程度，激发学生的学习兴趣和求知欲，活跃思维，提高学生学习的主动性；目标是提高学生利用知识解决实际问题的能力，培养学生的创新意识、创新思维和创新能力［4］。“高等数学”课程中的理论和方法都源于实际生活和生产实践，与专业课程的知识紧密相连。引导学生从实际生活和生产实践中发现问题，是可行且具有重要意义的事情。在“高等数学”课程教学中以问题驱动为切入点，可以培养学生在实际中发现问题的习惯和思维，进而激发学生的求知欲望。学生掌握了解决问题的知识和理论方法后又可以解决很多实际问题，增强学习的成就感和能力提升的自信心。

然而，如何选择问题驱动教学案例是很关键的问题。由于“高等数学”是工科专业学生的公共必修课，如果教师能够根据不同专业的特点从专业课程中寻找到合适的案例作为问题导入课程，既体现问题驱动又体现专业导向，在激发学生学习兴趣、引发学生好奇心的同时，又能让学生感受到学习高等数学知识对学习专业知识的重要性，提高学生对高等数学學习的重视程度，同时又能为学生更好地学习专业知识打下坚实的基础，达到“一箭双雕”的目的。这样的教学安排既能够激发学生学习高等数学的热情，又为学生顺利学习专业知识做好铺垫，能够增强学生学习专业课程的信心。总之，在“高等数学”课程教学中以问题驱动为切入点，以专业导向为着力点，可启发学生从实际生活和生产实践中发现问题、引发思考，进而分析问题和解决问题，最终为实际生产生活服务，体现出专业导向。通过问题驱动和专业导向的设置，学生解决问题的能力得到了提升，同时培养了创新能力。

四、建设以问题驱动和专业导向的“高等数学”课程的策略

（一）引例提问，突出专业导向

导入新课的方式有很多，如直接导入、温故导入、直观导入、情境导入、问题导入、实例导入、故事导入等。好的课堂导入可以抓住学生眼球，吸引学生注意力。课堂导入的目的是学习新知识，故而不能盲目地导入、为了导入而导入。在“高等数学”课程建设过程中要突出问题驱动和专业导向，结合实例导入、问题导入两种方法。

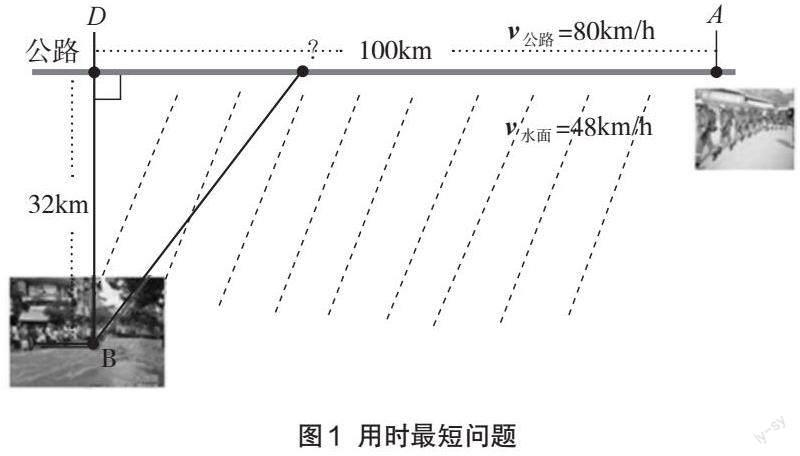
比如，在讲授函数的最大值最小值时，可引入两个引例。引例1（用时最短问题，如图1）：假设现有一支救援队伍要从A地出发，经过一片水域到达B地去营救被困人员。已知A、D间的公路距离为100 km，D、B之间的垂直距离为32 km，公路上行驶的速度为80 km/h，水路上行驶的速度为48 km/h。试问救援人员应从A、D之间的哪个点处换走水路用时最短？引例2（利润最大问题）：一房地产公司有50套公寓要出租：当月租金定为4 000元时，公寓可以全部租出去；当月租金每增加200元，就会多一套公寓租不出去。租出去的公寓每月需花费400元的维修费。试问房租定为多少可获得最大收入？通过这两个引例让学生意识到在实际生活中会经常遇到求用时最短、容积最大、利润最大、用料最省等问题，这些问题都可以归结为求某一函数的最值。从这些实际问题中，学生可以看出学习求函数最值方法的意义，自然会产生如何求函数的最值的疑问，由此激发学生的求知欲望和学习兴趣，吸引学生的注意力，为讲授新知做好铺垫。

（二）储备知识，打好基础

解决问题必须储备知识、打好基础，因此在“高等数学”课程的教学过程中，教师应突出重点、突破难点。以函数的最大值最小值内容为例，在教学的过程中，教师可根据内容的需要从两方面引导学生得到结论：（1）对于一般函数，可以很容易得出：函数的最大值最小值点总是在极值点或区间端点处。由此，结合函数极值的求法，可以得到求函数最值的步骤。（2）对于实际问题，从函数的驻点与极值点的关系可以得出：如果最大（小）值存在且驻点唯一，那么这个驻点就是最大（小）值。这个结论可以保证在计算时只需计算出驻点，不需判定其是否为极值点，就能判定是否为最大（小）值点，减少了计算量。掌握了这些知识之后，学生就能解决引例中的问题。

（三）求解引例，解决问题，突出专业导向

引用实例是为了提出问题，引发学生思考。为了解决导入部分的提问，学生需要对提出的问题进行解答。在解答问题的过程中，学生可以感受到知识的应用价值，也能认识得到专业课程学习中需要知识基础，在学好“高等数学”课程的同时，要更好地学习专业知识。

总之，这样的课程教学体现了问题导入、学以致用、首尾呼应的特点。教学过程紧紧围绕问题驱动和专业导向展开，目的是以问题驱动引发学生思考，从实际中发现问题，让学生意识到学习新知识的必要性，激发学生学习新知识的兴趣，提高学习热情；学习完新知识之后，利用新知识求解引例能够让学生体会新知识的应用价值，从而深刻地感受到学习新知识的意义。这种前后呼应的设计可以产生学习闭环，使学生明确学习目标和动机。这种模式的课程建设极大地体现了高等数学知识和专业课程知识的衔接，体现了专业导向的宗旨，有利于培养多元化的创新型人才，可以满足新工科背景下对人才的需求。

五、“高等数学”课程建设中需要改变的方向

（一）改变传统的教学模式

只有改变现有的、传统的教学模式，从“以教师为中心”的教学模式转变为“以学生为中心”的教学模式，学生才能从被动地学习高数知识转变为为解决问题而主动学习。教学模式的转变能够使学生体会到数学知识的应用价值，提高了解决问题的能力，也培养了学生的创新能力。

（二）改变教师的教学理念

在传统的教学理念中，“高等数学”课程的任课教师认为只要教会学生本门课程的知识就够了，不重视知识的应用及与其他学科的衔接。为了适应新工科的发展需求，教师应改变这种教学理念，在讲授高等数学知识的同时，努力展现高等数学知识与专业课程知识的联系，使学生明白学习高等数学知识的重要性和意义。这不仅可以提高学生高等数学知识的学习热情，还可以激发学生对专业知识的学习兴趣，起到事半功倍的效果。

（三）改变课堂教学的内容

现有的高等数学教材只包含高等数学知识，其中的实例大多比较陈旧、枯燥，没有与时俱进，无法体现与专业课程的关联。为了更好地体现出“高等数学”课程与专业课程的联系，教师应选择一些专业课程知识融入课堂教学，通过知识点的有机融合，适当调整课堂教学内容，体现高等数学知识的重要性及其与专业课程知识的联系，让学生在高等数学知识和专业课程知识方面都能取得更好的学习效果。

结语

新工科要求把培养时代和未来所需的创新型卓越人才摆在更加突出的战略位置，为实现中国梦和应对复杂多变的世界提供智力支撑和人才保障。未来几十年，科技进步和创新将成为推动人类社会发展的重要引擎［1］。科技进步和创新都需要依靠工科专业的人才，而要培养出多元化、创新型的卓越人才，学科之间的交叉与融合是必然趋势。以问题驱动和专业导向为重点建设“高等数学”课程，就是要促进学科之间的交叉与融合，促进学生具备更扎实的专业知识，同时引导学生从生活和生产实践中发现问题，并为了解决问题学习新知识、利用新知识。这样的课程必能为培养学生的专业素养和基本技能做好服务，从而为满足新工科背景下培养多元化、创新型卓越人才做好准备，促进工程科技的进步和创新。因此，建设以问题驱动和专业导向的“高等数学”课程具有非常重要的意义，是一项重要的工作。

參考文献

［1］黎锁平，焦桂梅，周永强，等.新工科理念下高等数学能力培养型教学改革研究［J］.高等理科教育，2021（1）：81-85.

［2］钟登华.新工科建设的内涵与行动［J］.高等工程教育研究，2017（3）：1-6.

［3］陈莉，栗青生.新工科背景下以专业为导向的高等数学教学改革［J］.科技资讯，2020，18（31）：158-159+162.

［4］张志海，庞培林，栗文国.问题驱动下高等数学教学之我见［J］.河北工程大学学报（社会科学版），2018，35（3）：100-101.

［5］刘生全.问题驱动教学模式应用于高等数学课程探究［J］.吉林化工学院学报，2021，38（10）：19-22.

Abstract： Based on the traditional problems existing in the teaching of higher mathematics， the importance of integrating higher mathematics course with professional course under the backgrourd of emerging engineering， the construction meaning of new curriculum based on problem-driven and porfession-oriented methods， how to carry out higher mathematics course construction and the directions that need to be changed， the construction higher mathematics curriculum is deeply explored. Taking the content of maximum and minimum value of function as an example， this paper explains how to construct higher mathematics course from the three links of introducing new course， teaching new knowledge and consolidating new knowledge， so as to meet the demand for diversified and innovative talents in the background of emerging engineering education.

Key words： emerging engineering education; “higher mathematics”; curriculum construction; problem-driven; profession-oriented