以计算思维为中心的数据结构教学方法探讨

沈华　张明武

摘要：如何帮助学生学习和掌握数据结构课程蕴含的计算思维，是从事数据结构教学工作的教育者需要考虑的重要问题。文章提出一种基于问题驱动和图示法的教学方法，即以计算思维为中心的教学方法，以稀疏矩阵的转置问题为例说明该教学方法的理念和特点。

关键词：数据结构；计算思维；教学方法；问题驱动；图示法

0引言

在计算机科学中，数据结构是一种在计算机中组织和存储数据，以便高效利用这些数据的有效方式。数据结构主要研究数据在抽象视图和实现视图中的表示和处理方法，其理论性和抽象性较强，要求能够运用计算思维分析并解决问题，被认为是比较难学的课程。基于问题驱动的教学方法是将求解原问题转换成一系列的子问题，通过求解子问题序列最终求解原问题，子问题序列实际上给出运用计算机求解问题的最终目的和思考问题的计算思维轨迹。图示法可以直观、形象地描述每个子问题的求解思路和过程。为了让学生更好更明确地理解什么是计算思维、数据结构中有哪些计算思维、怎样运用计算思维求解问题，通过在教学过程中不断尝试和探索，我们发现将问题驱动与图形演示两种教学手段结合起来是一种行之有效的教学方法，即以计算思维为中心的教学方法。

1问题描述

随机稀疏矩阵是非零元比零元少很多且非零元的分布不具规律性的一种矩阵，转置矩阵是矩阵行列交换后得到的一种矩阵。通常用二维数组表示矩阵，借助二维数组可以实现计算机求解矩阵的转置矩阵。以求解稀疏矩阵M的转置矩阵T为例，求解过程如图1所示。

实现求解稀疏矩阵M的转置矩阵T这个目标，需要依次解决的子问题有在存储器中如何存储二维数组、如何以低空间成本存储稀疏矩阵、如何从存储结构的角度解读需要求解的问题和如何求解新视图中的问题。

2教学过程

按照求解逻辑，将求解稀疏矩阵的转置矩阵问题细化为一个子问题序列，通过依次求解序列中的子问题最终使原问题得到解决。讲解每个子问题的求解方法时，可以运用图示生动形象地描述抽象复杂的求解过程。具体教学过程如下所述。

1）子问题1：如何在存储器中描述二维数组。

这个子问题隐藏的计算思维是如何在线性空间（存储器）中描述非线性结构。为了更形象地说明该子问题的两种求解方法——“以行为主”顺序存储和“以列为主”顺序存储，我们在讲解的过程中使用图2所示的示意图。

2）子问题2：如何以低空间成本存储稀疏矩阵。

随机稀疏矩阵中的非零元非常少，为了节约空间成本，通常只存储其中的非零元信息，但非零元在矩阵中的分布没有规律性，因此除了需要存储非零元的值外，还需要存储非零元在矩阵中的位置信息；三元组（行，列，值）结构可以满足这样的存储需求。一个稀疏矩阵可以表示为一个三元组集合，但三元组集合只给出了稀疏矩阵所有非零元的分布信息、值的信息和部分零元的分布信息，并不能唯一确定一个稀疏矩阵。为了获得所有零元的分布信息，我们需要知道稀疏矩阵的规模信息，即它是多少行多少列的矩阵。低空间成本存储稀疏矩阵M的存储结构图（以“行序为主”存储三元组）如图3所示。

3）子问题3：如何重新解读所求问题。

稀疏矩阵的转置矩阵还是稀疏矩阵，因此目标矩阵T也将按照上述低空间成本存储方案进行存储，那么用存储结构视图重新解读问题“已知稀疏矩阵M，求它的转置矩阵T”，实质上就是已知图3补全图的问题。

4）子问题4：如何根据图3的信息补全图4。

显然，根据M中m、n和t这3个成员的值可以很容易得到T.m、T.n和T.t的值，即T.m=M.n，T.=M.m，T.t=M.t。因此，我们需要解决的关键问题是如何根据M.data[]得到T.data[]。

解决方法1：以T.data[]为主导进行填充，即依次填充T.data[0]、T.data[1]……T.data[T.t-I]，并且保证存储是以T的“行序为主”顺序存储的。具体来说，需要对M.data[]进行M.n次扫描，第j（0≤j≤M.n-1）次扫描的任务是将M.datar 1中第j列的元素依次进行行列转换后插人T.data[]中。具体求解过程如图5所示。

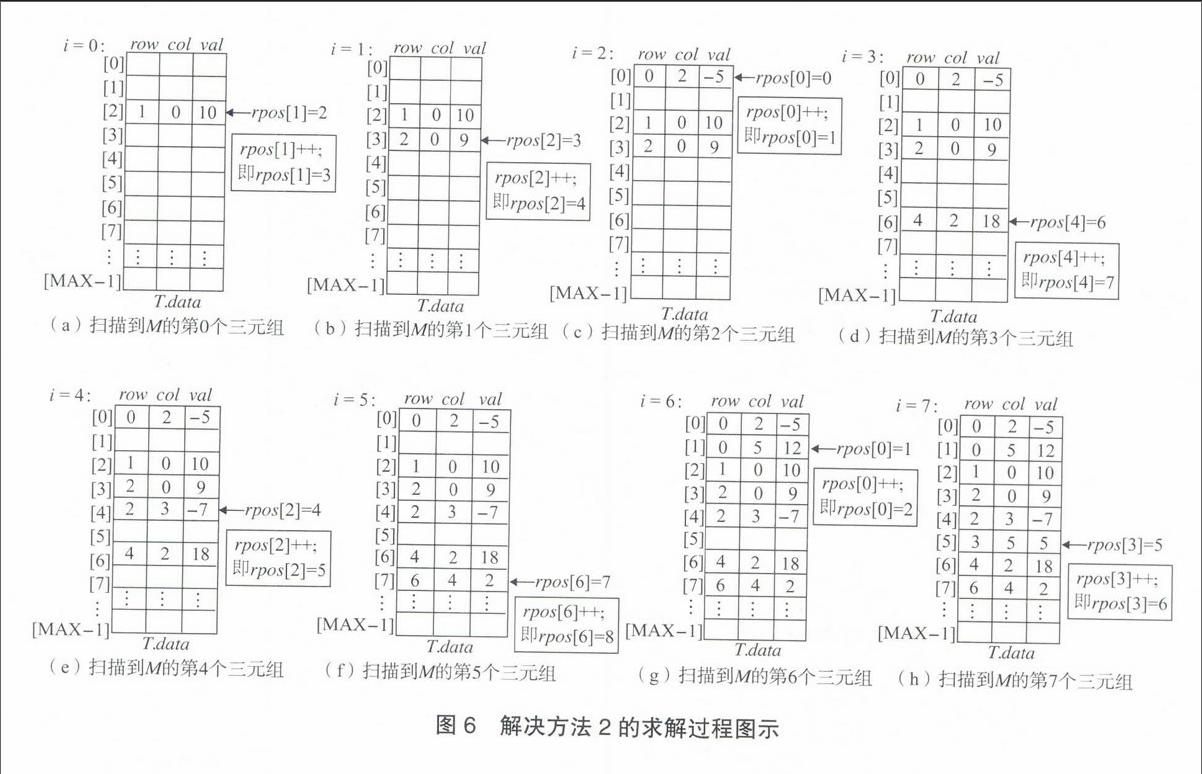
解决方法2：以M.data[]为主导进行填充，即依次根据M.data[0]、M.data[1]……M.data[M.t-11填充T.data[]，并且保证存储是以T的“行序为主”顺序存储的。具体来说，只需要对M.data[]进行一次扫描，扫描到第k（0≤k≤M.t-1）个三元组时，需要确定该三元组进行行列转换后的新三元组应该填到T.data[]中的什么位置。为了解决这个问题，在填充之前需要对M.data[]中的三元组进行统计分析，分析出M的每一列有多少个元组。假设得到M的第j（0≤j≤M.n-1）列有Nodesj个非零元，那么，实际上得到T的第f（0≤i≤T.m-1）行非零元在T.data[]中的位置范围为

为了便于操作，给每个位置范围设置—个“坐标指针”，用符号rposi（0≤i≤T.m-1）表示T的第i行坐标指针。坐标指针的作用是指示T的每一行当前需要填充的位置坐标，其移动轨迹为从相应位置范围的下界朝上界的方向移动，每次只能向后移动一个位置。具体求解过程如图6所示。

显然通过依次思考并求解上述4个子问题，最终可以利用计算思维成功求出稀疏矩阵M的转置矩阵T。 3结语

数据结构是一门理论性和抽象性都很强的课程，蕴含着很多的计算思维，如何帮助学生在学习数据结构时体会和掌握这些计算思维，是从事数据结构教学工作的教育者需要考虑的重要问题。我们在网络工程专业近5届共10个班的数据结构教学中采用该教学方法，学生普遍反映这样的教学方式不仅让他们了解如何运用某种数据结构解决一个应用问题，还让他们明白为什么会是这样的求解过程，更使他们明白如何将应用问题转换为计算机视角的等价问题，真真切切地感受到“计算思维”。此外，每年两个班中平均有近30%的学生入选学院ACM训练班，多名学生在各类软件设计大赛中获奖。可见，以计算思维为中心的教学方法在数据结构课程教学过程中是行之有效的。

（编辑：宋文婷）