“数的运算”教学思考

路叶娜

摘 要：小学阶段“数的运算”相关内容具有高度的一致性，彼此间联系紧密。在对其进行整体分析的基础上，提出教学策略：在情境与实例中感悟运算的意义，在算法融通中理解算理，在板块递进中感悟运算的本质。教学架构如下：分为“整数运算”“小数运算”“分数运算”这三个板块以及加减法、乘法、除法等子板块；对每个板块立足数学核心素养，整合目标、任务、情境与内容，划分出关键的教学单元，进一步形成教学活动链。

关键词：小学数学；数的运算；整体；结构化；单元教学

《义务教育数学课程标准（2022年版）》在“课程理念”中指出：课程内容组织的“重点是对内容进行结构化整合，探索发展学生核心素养的路径”［1］。又在“教学建议”中指出：“在教学中要重视对教学内容的整体分析，帮助学生建立能体现数学学科本质、对未来学习有支撑意义的结构化的数学知识体系……通过合适的主题整合教学内容，帮助学生学会用整体的、联系的、发展的眼光看问题，形成科学的思维习惯，发展核心素养。”［2］

小学阶段“数的运算”相关内容具有高度的一致性，彼此间联系紧密。本文尝试对其进行整体分析，进而提出教学策略，并进行教学架构。

一、“数的运算”的整体分析

首先，从现实意义来看，人们通常根据数量之间的关系，运用数的运算的算理与算法来解决现实生活中的问题。从在现实生活中产生数的概念，到建立数的运算体系，再到运用数的运算解决现实生活中的问题，体现了数学来源于生活又广泛

运用于生活的循环过程。

其次，从数学基础来看，数的运算是基于数的概念以及十进位值制记数法形成和发展的。根据数的实际意义、计数单位和数的组成，数与数之间可以定义运算，并形成算理和算法。例如，苏教版小学数学一年级下册第六单元《100以内的加法和减法（二）》的例3（如图1所示），便引导学生从现实情境出发，结合计数单位和数的组成（及其实物、图像、符号等多种表征），抽象建立相应的运算法则。此过程中，便蕴含着算理。

再次，从内部体系来看，数的运算分为整数运算、小数运算、分数运算三个板块；小数运算、分数运算以整数运算为基础，与整数运算既有联系又有区别；随着数的范围的不断扩大，运算法则在原有的整数运算法则的基础上不断扩容、贯通，最终形成数的运算的整体结构。

此外，学生在“数的运算”各个板块的学习过程中，都要经历一步运算、组合运算（混合运算）、运算规律探究和运用这三个层次的认识深化过程。

最后，整体来看，小学阶段“数的运算”的教学目标可梳理如下：（1）知道各种运算的意义，掌握各种运算的一般法则，形成基本计算技能；（2）感悟同种运算不同方法、不同运算之间的联系，发展数学思考；（3）根据不同的情境灵活选择合适的算法（估算、巧算等）解决问题，在规律探究中进一步完善能力建构，发展数学核心素养。

二、“数的运算”的教学策略

（一）在情境与实例中感悟运算的意义

加法是把两个或两个以上的数、量合起来，变成一个数、量的运算。减法是从一个数量中去掉另一个数量的运算，或者已知两个加数的和与其中一个加数，求另一个加数的运算。乘法是将相同的数、量加起来的快捷方式。除法是减去相同的数、量的快捷方式，或者已知两个因数的积与其中一个因数，求另一个因数的运算。

加减乘除的意义对于小学生来说，过于抽象。要让学生形成清晰的概念，需要联系学生的生活经验：一方面，通过具体情境得到算式例子，归纳提炼相同的本质属性，进而形成运算概念；另一方面，针对算式例子联想具体情境，从而丰富对运算意义的认识。

在建构运算意义的过程中，要结合与学生生活经验密切联系的实际问题，有机渗透数量关系；同时，在抽象与演绎的过程中，发展学生的抽象和推理等关键能力。

（二）在算法融通中理解算理

理解运算意义，是具体探究算法、深入理解算理的前提。苏教版小学数学教材中运算教学的设计，都是从实际问题引入，将问题的解决转化成相应算式的计算，在寻求计算结果的过程中，组织学生经历学具操作（摆小棒、拨计数器等）、符号记录以及口头言说计算思考的活动，生成不同形式的算法；各种算法之间异中有同，通过沟通关联，学生建立算法之间的内在联系，进而深入理解算理，由此让思维不断从直观向抽象发展。

此外，还有从一道算式（例题）的解决到同类一组算式的感悟，最终抽象形成一类计算的一般方法（口算方法、笔算方法）。同时，在数的运算的不同学习阶段，逐步渗透、落实估算、简算等灵活方法，发展和提升学生的运算能力。

（三）在板块递进中感悟运算的本质

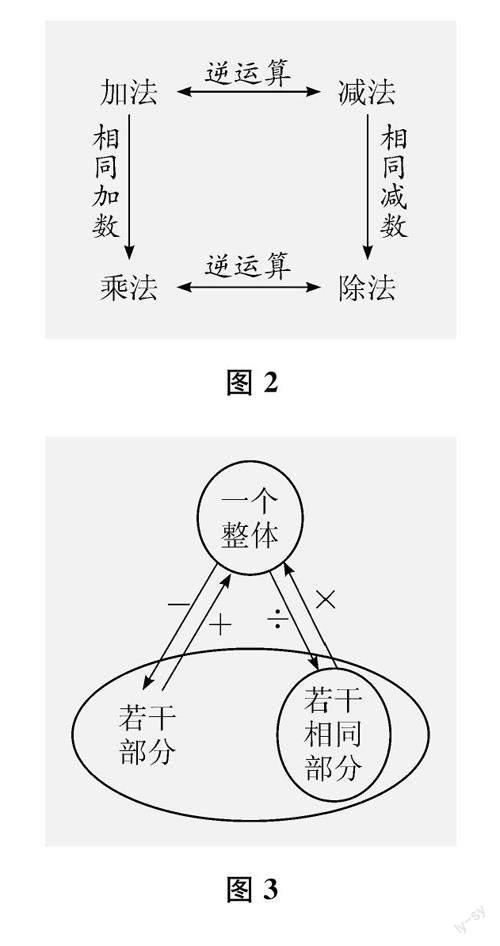
结合四则运算的意义，我们不难发现，乘法就是相同加数相加的简写，而除法也可以理解为不断减去同一个数（不完全除）；同时，加法与减法互为逆运算，乘法与除法亦然。其内在关联如图2和图3所示。

此外，我们还可以结合整数、小数、分数加减乘除的一般算法进一步剖析：加减法为什么要数位对齐？为什么要通分？多位数的乘法为什么乘完还要相加？除法除到某一位不够商1时怎么办？……最终发现，其实又回到了数的运算发展的起点——计数单位。计数单位与相应的计数本质上是相乘的关系（乘法的意义是相同的东西合起来），所以，加减法本质上是相同的计数单位不变，相应的计数相加减（分配律的运用，或者说合并同类项）；乘除法本质上是计数单位相乘除得到新的计数单位，相应的计数相乘除得到新的計数（幂的运算法则的运用）；加减乘除中蕴含着计数单位的合成和分解。可见，运算的本质在计数单位中（或者说，算术的本质在代数中）。

因此，教学要引导学生在“整数、小数、分数”的板块递进（以及“加、减、乘、除”的子板块递进）中，经历从最初的“看山是山”（经验之谈）到中期的“看山不是山”（分解学习），到最后的“看山还是山”（认知的整合）的过程，实现从“双基”到“素养”的进阶，同时，实现从算术到代数的进阶。

三、“数的运算”的教学架构

我们尝试把“数的运算”分为“整数运算”“小数运算”“分数运算”这三个板块来进行教学架构。三个板块都是先学习加法和减法，再学习乘法和除法。

以整数运算为例，我们尝试将其分为加减法、乘法、除法这三个子板块：对每个子板块，由表及里地提炼出关键的教学单元（如下页图4所示）和教学活动链。

图4中的教学单元与教材中的单元有所不同：不只是依据内容划分的，而是立足数学学科核心素养，整合目标、任务、情境与内容划分的。或者说，一个单元就是一个指向素养的、相对独立的、体现完整教学过程的课程细胞。

以加减法子板块的第一单元为例。为了帮助小学起始年段的学生加深对数的理解，更好地理解加法和减法，在10以内的加减法中培养数感，发展数学思考，我们将教材中《分与合》《10以内的加法和减法》两个单元进行整合，穿插教学，进一步形成教学活动链（如图5所示）。

在小学阶段“数的运算”知识体系中，10以内数的分与合是十分重要的基础知识，直接关系到10以内数的概念的形成，以及10以内加减法的计算。教材将2—10各数的分与合集中编排，希望学生能较好地感悟“分”与“合”的思想，为以后理解四则运算的意义打下基础。但集中学习10以内数的分与合，不利于学生体会分与合的价值，较难激发学生学习的主动性；同时，使得学生接受学习的容量较大，增加了学生的记忆难度。

10以内数的分与合的意义正是加法和减法的支撑，因此，将教材内容重组，把10以内数的分与合与其对应的加减法的学习有机结合，以帮助学生体会学以致用的重要意义，并在掌握知识与技能的基础上了解学习方法结构，逐步培养序列化探究、自主迁移学习等能力，促进教学过程中教学目标与教学评价指向核心素养，实现进阶。相应地，学习内容也在缓冲下逐步增加，便于一年级学生逐步适应学习过程。其活动链中各个活动的目标设计如下页表1所示。

从表1中不难发现各个活动之间教学侧重的转变和要求的递进。在这一单元的活动链中，概念整体进入和对方法的循环递进使用，体现结构的灵活；从分合到加减法再到简单“部总”问题，由浅入深，体现结构的递进。这一设计重在学习成果的内化和思维品质的培养，实现素养本位单元整体设计的价值追求。

总之，整个“数的运算”的教学过程，都要注意横向的丰富与打开，纵向的递进与灵活，用结构化的教学使学生的思维走向灵动与清晰，从“带着学生学”走向“学生独立学”，从点状的探索认知走向链状的有序研究和深入感悟。

參考文献：

［1］［2］ 中华人民共和国教育部.义务教育数学课程标准（2022年版）［S］.北京：北京师范大学出版社，2022：3，85.