斜三角形的一个性质及应用——从一道2022年联考压轴题谈起

张志刚

(山东省宁阳县复圣中学,山东 泰安 271400)

题目(2022年雅礼十六校第一次联考第16题)在锐角三角形ABC中,sinA=2sinBsinC,则tanAtanBtanC的最小值是____.

本题考查解三角形、三角恒等变换以及多元函数最值等问题,突出考查逻辑推理、数学运算、数学建模等核心素养.试题设计清新简洁,构思别具匠心,解法灵动多变,饱含数学思想,呈现出较强的综合性与选拔性,具有较高的挖掘价值[1].

1 试题解答

思路1 运用消元思想转化为一元函数最值问题.

对于多元函数的最值问题,消元是最常见的思维方向和解题原则.

解法1 (借助三角形内角和定理消元)由sinA=2sinBsinC,即sin(B+C)=2sinBsinC.

即sinBcosC+cosBsinC=2sinBsinC.

等式两边同时除以cosBcosC,得

tanB+tanC=2tanBtanC.

令t=tanBtanC-1,又△ABC是锐角三角形,tanAtanBtanC>0,从而tanBtanC-1>0.

即t>0.

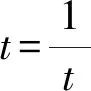
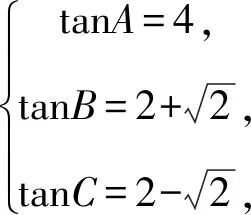
所以tanAtanBtanC的最小值是8.

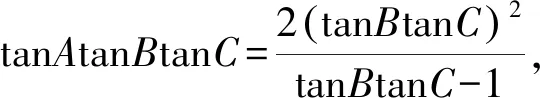
解法2 (构造等差数列消元)由sinA=2sinBsinC,即得sin(B+C)=2sinBsinC.

即sinBcosC+cosBsinC=2sinBsinC.

等式两边同时除以cosBcosC,得

tanB+tanC=2tanBtanC.

等式两边再同时除以tanBtanC,有

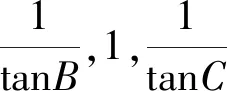
设此等差数列的公差为d,即

所以tanAtanBtanC的最小值是8.

思路2 运用斜三角形正切恒等式求最值.

本题探求三角形内角正切值之积的最值问题,联想到斜三角形的一个性质:tanAtanBtanC=tanA+tanB+tanC(以下简称“正切恒等式”),利用此等式可实现内角正切值“积”与“和”的互相转化.

解法3 (化积为和构造不等式)由sinA=2sinBsinC,即得sin(B+C)=2sinBsinC.

即sinBcosC+cosBsinC=2sinBsinC.

两边同时除以cosBcosC,得

tanB+tanC=2tanBtanC.

又△ABC是锐角三角形,tanB>0,tanC>0,由正切恒等式及基本不等式得

tanAtanBtanC=tanA+tanB+tanC=tanA+2tanBtanC

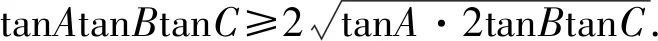
所以tanAtanBtanC的最小值是8.

点评解法3巧妙运用性质tanAtanBtanC=tanA+tanB+tanC,“化积为和”,结合已知条件“tanB+tanC=2tanBtanC”与基本不等式构造了关于乘积式tanAtanBtanC的不等式,使问题获解.在运用基本不等式求解最值时,要注意“一正、二定、三相等”条件的检验.

解法4 (化和为积构造不等式)由sinA=2sinBsinC,得sin(B+C)=2sinBsinC.

即sinBcosC+cosBsinC=2sinBsinC.

两边同时除以cosBcosC,得

由基本不等式,得

2tanAtanBtanC=tanA(tanB+tanC)

由正切恒等式,得

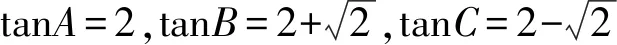
所以tanAtanBtanC的最小值是8.

点评本题探求三个内角正切乘积的最值,为此应用正切恒等式实现了“化和为积”,构造了关于乘积式tanAtanBtanC的不等式,解题效益大幅提高.

比较上述几种解法,解法1借助三角形内角和定理实现首次消元,再令t=tanBtanC-1进行二次消元,再结合基本不等式求得一元函数的最值,思维跨度较大,运算过程较为繁琐;解法2经历多次变形,敏锐发现了等差数列模型,进而设出等差数列的公差d,并最终将问题转化为关于d的一元函数最值,方法不可谓不妙,但需要考生丰富的想象能力和较强的运算求解能力;而思路2中的两种解法充分应用性质tanAtanBtanC=tanA+tanB+tanC,“化积为和”或“化和为积”,回避了思路1多次消元及换元的繁琐,思维简练,进退自如,简捷明快[2].

2 深化研究

思路2的正切恒等式源于普通高中标准实验教科书《数学·必修4·B版》(人民教育出版社2007年第2版)第154页第7题:

在斜△ABC中,求证:tanA+tanB+tanC=tanAtanBtanC.

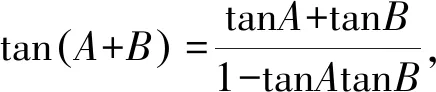
即tanA+tanB=tan(π-C)-tanAtanB·tan(π-C).

即有tanA+tanB+tanC=tanAtanBtanC.

正切恒等式揭示了斜三角形的一个独特、奇妙的结论:三内角正切值的乘积等于正切值的和.适时应用正切恒等式,对于解决三角求值、三角极值等问题发挥着重要作用.具体应用概括如下.

2.1 挖掘内涵,横向联系

正切恒等式沟通了斜三角形三个内角正切值的和与积的关系,利用它可实现二者的相互转化,便于解决一些问题.

例1 (2021年北京大学优秀中学生寒假学堂测试卷第17题)在锐角△ABC中,求tanAtanB+2tanBtanC+3tanAtanC的最小值.

解析由题意知,tanA,tanB,tanC>0,又tanA+tanB+tanC=tanAtanBtanC,可得

由柯西不等式,得

解析由(b-sinC)cosA=sinAcosC,得

bcosA=sinAcosC+cosAsinC.

即bcosA=sin(A+C)=sinB.

由正切恒等式,得

tanA+tanB+tanC=tanAtanBtanC.

即2tanBtanC=2+tanB+tanC.

在锐角△ABC中,tanB>0,tanC>0,由基本不等式,得

2tanBtanC=2+tanB+tanC

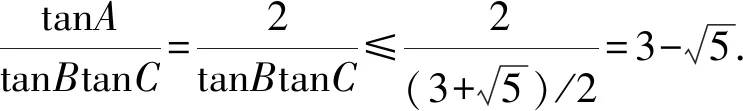
2.2 特殊赋值,演绎精彩

通过对正切恒等式中的角赋值,可得系列特殊三角形,衍生出诸多有趣结论.

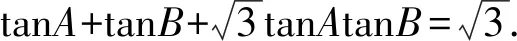
①

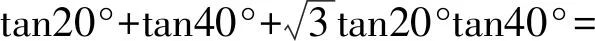
解析①式中令A=20°,B=40°,可得

例4 (2006年第17届“希望杯”全国数学邀请赛高一年级第1试第17题)

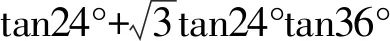
解析①式中令A=24°,B=36°,可得

解析①式中令A=10°,B=50°,可得

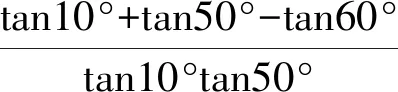
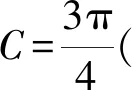
tanA+tanB-1=tanAtanB·(-1).

即tanA+tanB+tanAtanB=1.

即(1+tanA)(1+tanB)=2.

②

例6 (2008年南京大学自主招生第2题)(1+tan1°)(1+tan2°)…(1+tan44°)(1+tan45°)=____.

解析②式中令A=1°,B=44°,可得

(1+tan1°)(1+tan44°)=2.

令A=2°,B=43°,可得

(1+tan2°)(1+tan43°)=2,

…

令A=22°,B=23°,可得

(1+tan22°)(1+tan23°)=2,

于是(1+tan1°)(1+tan2°)…(1+tan44°)(1+tan45°)=223.

2.3 归纳推广,发现事实

通过对正切恒等式推广,可得如下结论:

等式两边同时取正切,得

tan(α+β)=tan(kπ-γ).

进而tanα+tanβ+tanγ=tanαtanβtanγ.

证明在△ABC中,A+B+C=π,可得

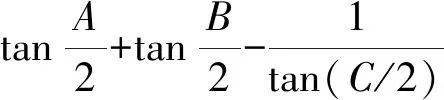
易知结论1的逆命题亦成立,即得结论2[3].

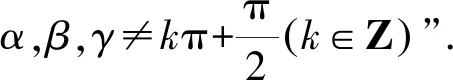
例8 (2015年全国高中数学联赛新疆赛区预赛高一第4题)已知α,β均为锐角,且(1+tanα)(1+tanβ)=2,则α+β=____.

解析由(1+tanα)(1+tanβ)=2,得

1+tanα+tanβ+tanαtanβ=2.

即tanα+tanβ-1=-tanαtanβ.

又α,β均为锐角,0<α+β<π,

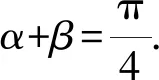
例9 (河南省中原名校2017-2018学年第一次质量考评高三理科第17(1)题)△ABC的内角A,B,C的对边分别为a,b,c,已知(1-tanA)(1-tanB)=2,求角C.

解析由(1-tanA)(1-tanB)=2,得

tanA+tanB+1=tanAtanB.

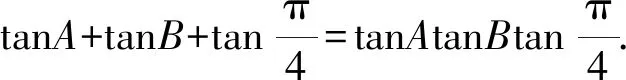
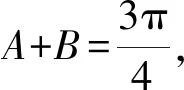
通过以上分析可以看出,应用正切恒等式无疑会有效突破思维瓶颈,降低思维难度、大幅减少运算量,加快解题进程,促使问题顺利解决.