借双慧眼识“隐圆”

孟方明

(浙江省春晖中学,浙江 绍兴 312300)

数学解题的关键是善于挖掘已知条件的“内涵”,即所谓的隐含条件.在某些数学问题中,虽然从表面看已知条件与圆“毫无关系”,但如果对问题进行深入的观察、分析和转化,就能发现圆的踪迹.识“隐圆”,用“隐圆”能帮助我们打开解题思路,提升处理数学问题的能力.

1 圆的解码

1.1 圆的两个定义

(1)第一定义:平面内到定点的距离等于定长的点的轨迹.

(2)第二定义:平面内到两定点的距离之比是一个不等于1的常数的点的轨迹(阿波罗尼斯圆).

1.2圆的两种方程

(1)标准方程:(x-a)2+(y-b)2=r2,其中(a,b)是圆心,r为半径.

(2)一般方程:x2+y2+Dx+Ey+F=0,其中D2+E2-4F>0.

1.3 圆的基本性质

(1)直径所对的圆周角是直角.这表明若动点C对两定点A,B成直角,则点C在以AB为直径的圆上.

(2)同弧所对的圆周角大于圆外角.这表明若动点C在过两定点A,B的某个圆外或圆上,则∠ACB的最大值是圆周角.

2 化隐为显,“圆”来相会

2.1 通过定义发现圆

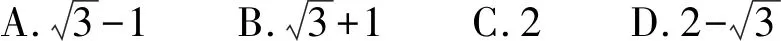
图1 例1解析图

由b2-4e·b+3=0,

配方得(b-2e)2=1.

即|b-2e|=1.

所以点B的轨迹是以点C为圆心,半径为1的圆.

点评本题关键是要将向量等式b2-4e·b+3=0转化为定长问题,从而可由圆的第一定义发现动点轨迹是一个圆,再利用圆上点到直线距离的最小值等于圆心到直线距离减去半径[1].

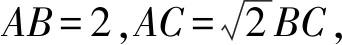
图2 例2解析图

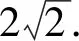
2.2 借助方程显示圆

例3 已知实数a,b,c满足a+b+c=0,a2+b2+c2=1,则a的最大值是____

解析因为a2+b2+c2=1,则a2≤1.

但是若a2=1,则导致b=c=0,与已知矛盾,所以a2<1.

注意到a2+b2+c2=1的结构与圆方程x2+y2=r2类似,由a2+b2+c2=1,得b2+c2=1-a2.

点评本题是多元约束条件下的最值问题,欲求a的最值,将b,c视为主元,通过b2+c2=1-a2这个形式的方程确定圆心在原点的“隐圆”,从而顺利地通过直线与圆的位置关系,突破此题.

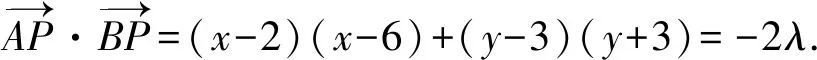
解得(x-4)2+y2=13-2λ.

由已知直线l与圆M相交.

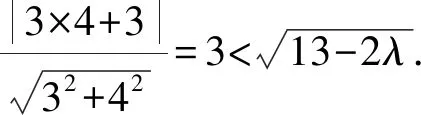
解得λ<2.

点评当平面内的一个动点与两个定点构成的数量积是定值时,一般就可以由动点满足的轨迹方程确定“隐圆”,求解数量积下的“隐圆”问题,关键是构建解析几何与平面向量等不同知识间的联系,实现问题的无缝链接.

2.3 基于性质构造圆

例5 在平面直角坐标系xOy中,直线ax+by+c=0被圆O:x2+y2=16截得的弦的中点为M,且满足a+2b-c=0,则|OM|的最大值是____.

解析由a+2b-c=0,直线方程可改为

a(x+1)+b(y+2)=0.

由此可知直线l恒过定点P(-1,-2).

点评因为直径所对的圆周角为直角,所以当题目出现动点对两定点张角为直角的情况时,就能得出动点轨迹是以这两点为直径端点的圆.从本题来看,只要能发掘出直线过定点P以及注意到MO⊥MP,“隐圆”就无处遁形.

(1)求椭圆的方程;

(2)设P为直线l:x=m(|m|>1)上的动点,使∠F1PF2最大的点记为Q,求点Q的坐标(用m表示).

图3 例6解析图

点评同圆弧所对圆周角大于圆外角是圆的一个基本性质,对某些张角最大值问题,若巧用这一性质,则可迅速锁定最值位置.本题关键在于由∠F1QF2恒大于∠F1PF2,构造过点F1,F2且切于点Q的“隐圆”,与传统函数不等式解法相比,此法事半功倍[2].

综上,对于“隐圆”问题,我们从定义、方程、性质三个角度进行了剖析和处理,确定“隐圆”的途径和方法,关键还是要抓住圆的重要特征,结合圆的有关知识方法,从而让隐形圆无法隐形,“圆”形毕露,正所谓:有“圆”千里来相会,无“圆”对面不相逢.