一道模考题的逆问题及推广

重庆市铜梁二中 (402560) 田 飞 李 波

某校的高三模拟试卷中,解析几何题目如下:

已知点P(4,4)在抛物线C:y2=2px(p>0)上,直线l:y=kx+2与抛物线C有两个不同的交点.(1)求k的取值范围;(2)设直线l与抛物线C的交点分别为A,B,过点A作与C的准线平行的直线,分别与直线OP,OB交于点M,N(O为坐标原点),求证:|AM|=|MN|.

1.一般化及逆问题

笔者发现:(1)直线l过定点K(0,2);(2)直线KP恰好是抛物线C在点P处的切线.抓住这两个特点,考虑将第(2)问一般化.

性质1 如图1,过K(0,a)(a≠0)作抛物线C:y2=2px(p>0)的异于y轴的切线交C于点P,过K的另一直线l与C交于A,B两点,过点A作与y轴平行的直线分别交直线OP,OB于M,N,则|AM|=|MN|.

图1

在性质1中,“KP为切线”是关键的条件,自然的问题:性质1的逆是否成立?

性质2 过K(0,a)(a≠0)作直线l交抛物线C:y2=2px(p>0)于A,B两点,过点A作y轴的平行线交OB于N.设M是线段AN的中点,直线OM交C于点P,则KP是C的切线.

另一方面,抛物线C在P处的切线方程为yyP=p(x+xP),即px-2ay+2pa2=0.显然,点K在此切线上,即KP是抛物线C的切线.

2.推广

为了从更高的数学观点考察性质1,需要预先准备以下知识.

定义1(极点极线的几何定义)如图2,点P不是圆锥曲线Γ上的点,过P引两条割线依次交Γ于E,F,G,H,连接EH,FG交于N,连接EG,FH交于M,则直线MN为点P对应的极线.

图2

引理1 如图2,当点P在圆锥曲线Γ外时,过P引Γ的两条切线PA,PB,则切点弦AB所在的直线为P对应的极线.

引理2 如图2,MN为点P对应的极线,若过P的直线交MN于K,交Γ于G,H,则P,G,K,H四点构成调和点列.

在性质1中,KO,KP都是抛物线C的切线,由引理1知,OP是点K关于C的极线. 圆锥曲线的许多性质都能统一起来,那么,性质1能否推广到一般情形,椭圆和双曲线上是否有相似的结论?针对这个问题,下面将在椭圆上给出肯定的回答.

性质3 如图3,设点K是椭圆L外任意一点,K关于L的极线交L于P,Q两点,过K作直线l1交L于A,B,过A作直线l2//KQ交PQ,QB于M,N,则|AM|=|MN|.

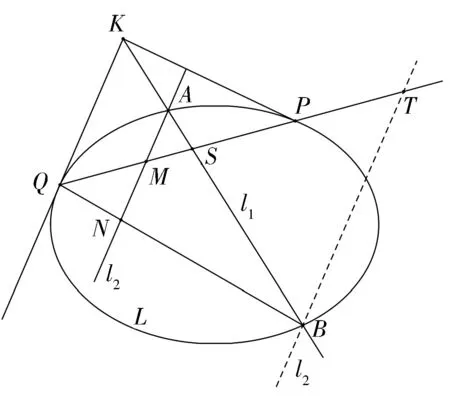
图3

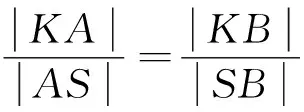
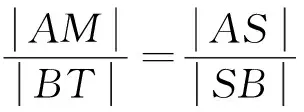
当点K在椭圆L内时,有

性质4 如图4,设椭圆L内任意一点K关于椭圆L的极线为l,过K的直线交l于点T,交L于A,B两点,过T作L的切线且切点为P,过A作平行PT的直线且分别交BP,KP于N,M,则|AM|=|MN|.

图4

由于K的极线l上任意一点关于椭圆L的极线必过点K,且切点P是T关于L的极线上的点,故KP是T关于L的极线. 因此T,A,K,B构成调和点列. 从而,性质4仿照性质3的证明得到.

如果我们认为,双曲线两支的中间部分是双曲线内,两边是双曲线外,那么双曲线上也有与性质3和性质4平行的结论.

性质5 设双曲线L外任意一点K关于椭圆L的极线为l,过K的直线交l于点T,交L于A,B两点,过T作L的切线且切点为P,过A作平行PT的直线且分别交BP,KP于N,M,则|AM|=|MN|.

性质6 设点K是双曲线L的内任意一点,K关于L的极线交L于P,Q两点,过K作直线l1交L于A,B,过A作直线l2//KQ交PQ,QB于M,N,则|AM|=|MN|.