定积分视角例析几道不等式问题的证明
2023-07-19 02:43广东省深圳市盐田高级中学518081陈一君
中学数学研究(江西) 2023年8期
广东省深圳市盐田高级中学 (518081) 陈一君
众所周知,定积分有其直观明了的几何意义以及简明性质.在教学中发现,以定积分的视角,借助定积分的几何意义与相关性质来审视某些不等式的证明,可以得到这些不等式简洁明快的证明过程,且具别开生面之感.本文对一些不等式通过定积分视角予以证明,以供教学参考.
例1 若a,b>1,证明ea-1+blnb≥ab.
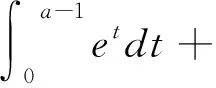

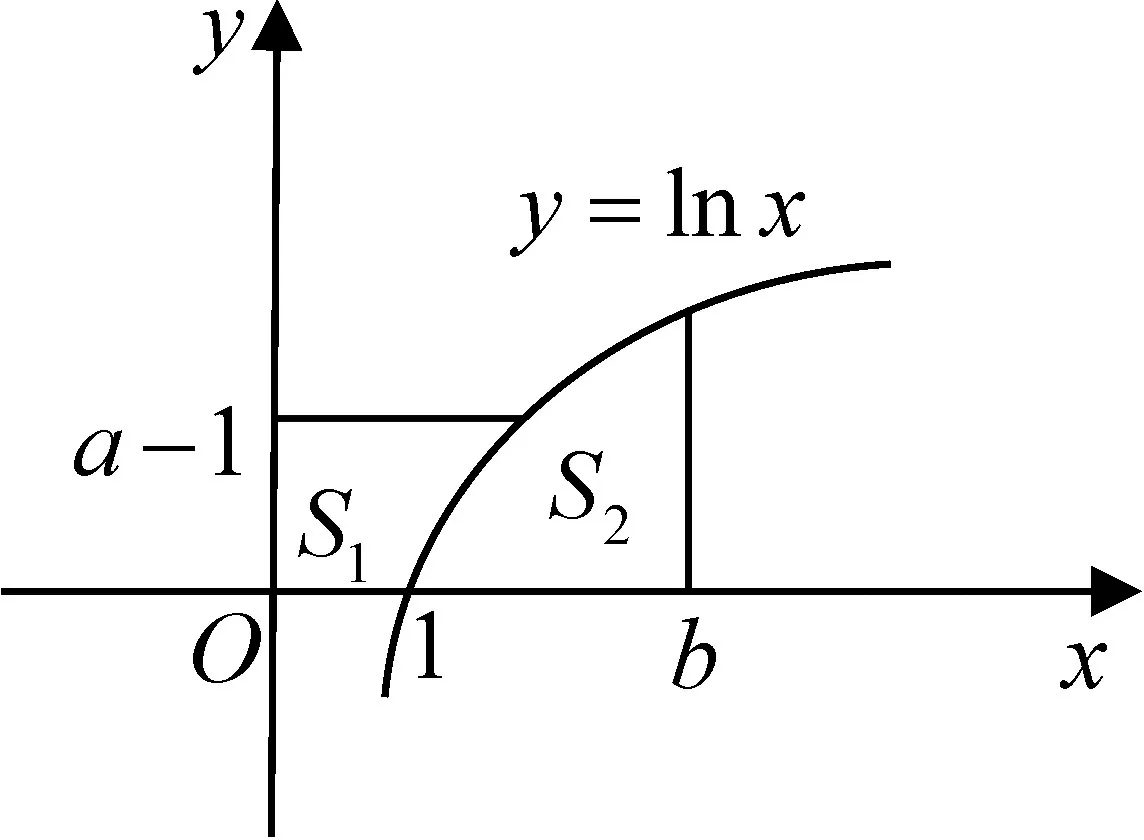
图1
评析:上述证法的关键在于,以定积分视角审视不等式,揭示不等式结构中隐含的定积分元素,从而借助直观的面积不等关系证得不等式.

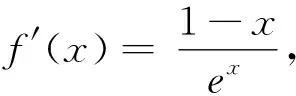
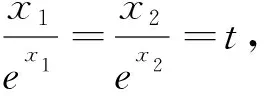

图2
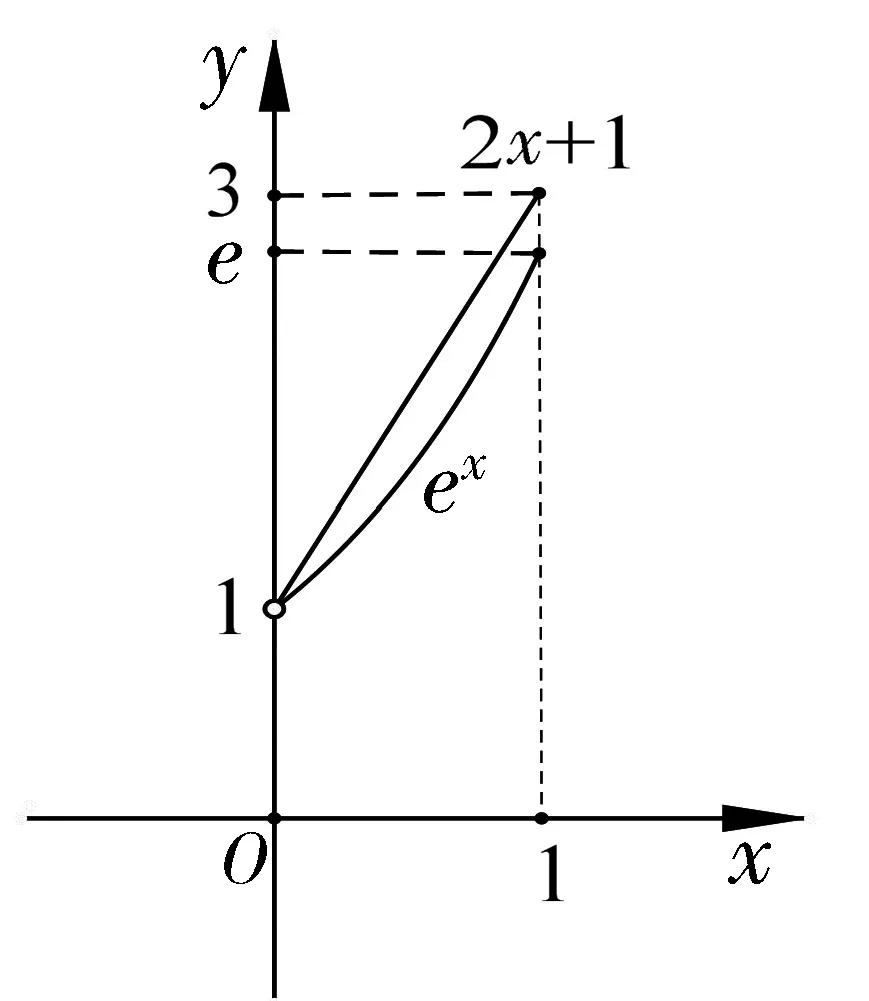
评析:上述证法,首先需要借助导数,明确f(x)单调性,从而得到隐含条件0 图3 评析:上述证明的关键在于从定积分视角,仔细审视不等式结构,由图形中析取蕴含其中的不等关系. 评析:上述证明的关键是通过两种不同情形,得到不等式后,利用定积分性质,得到其证法. 评析:本例是熟知的对数均值不等式,其证明依托定积分性质,给人耳目一新之感. 简析:(1)因为f(0)=1-a<0,f(2)=e2-2-a≥e2-4>0,所以y=f(x)在(0,+∞)上存在零点.因为f′(x)=ex-1,所以当x>0时,f′(x)>0,故函数f(x)在[0,+∞)上单调递增,所以函数以y=f(x)在(0,+∞)上有唯一零点. 图4 评析:本题为浙江省2020年的高考压轴题,上述证明是基于定积分性质给出的,显见其证明更简便快捷.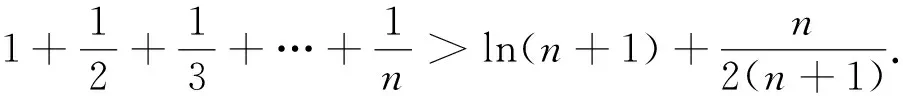

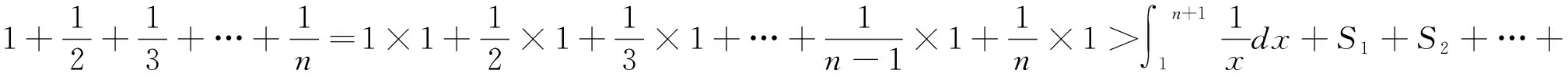



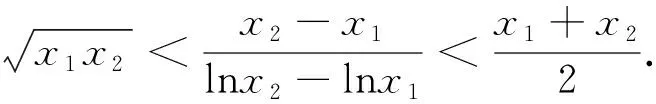

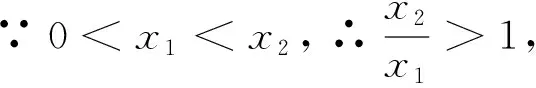

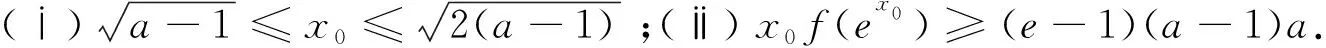
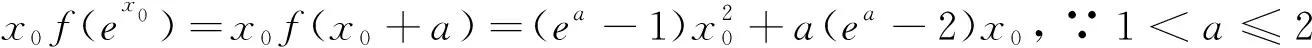
猜你喜欢
天府数学(2020年3期)2020-09-10
河北理科教学研究(2020年1期)2020-07-24
数理化解题研究(2020年13期)2020-05-07
数学物理学报(2019年5期)2019-11-29
中国医疗保险(2018年3期)2018-07-14
中共南昌市委党校学报(2016年1期)2016-11-24
数学学习与研究(2016年1期)2016-07-04
读写算(中)(2016年9期)2016-02-27
中国工程咨询(2011年5期)2011-02-16
物理与工程(2010年5期)2010-03-25

