两道几何命题的新证、类比与推广

广东省深圳中学 (518001) 邱际春

1 提出问题

第19届美国数学奥林匹克第5题是一道优美的几何赛题,摘录如下:

题目平面上给定一个锐角ΔABC,以AB为直径的圆与AB边上的高线CC′及其延长线交于M、N,以AC为直径的圆与AC边上的高线BB′及其延长线交于P、Q．证明:M、P、N、Q四点共圆．

笔者在文[1]和文[2]中利用多种方法分别证明了原赛题,并在文[3]中针对此题的基本图形进行改造,衍变得到一些有意义的几何命题．

下面摘录文[3]的两个几何命题:

命题1 如图1,在锐角三角形ΔABC中,以AB为直径的圆Γ1与AC相交于点E,以AC为直径的圆Γ2与AB相交于点F,BE与CF交于点H,且AH交EF于G,O为ΔAEF的外心．证明:CO⊥BG．

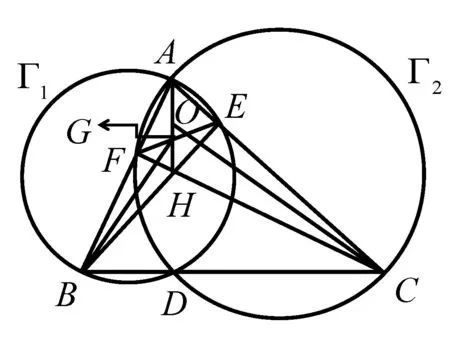
图1

命题2 如图2,在锐角三角形ΔABC中,以AB为直径的圆Γ1与AC相交于点E,以AC为直径的圆Γ2与AB相交于点F,BE与CF交于点H,且AH交EF于点G,若O为ΔAEF的外心,延长BO交AC于点L,延长CG分别交BO、BE于点M、N．证明:LN//OH．

图2

本文基于三角函数的视角重新证明上述两个几何结论,并对此作进一步类比探究,得到新的推广结论．

2 命题新证

事实上,我们根据图形结构特征容易看出命题2是由命题1引申得到的结果．下面利用三角法给出上述命题1和命题2的新证明．

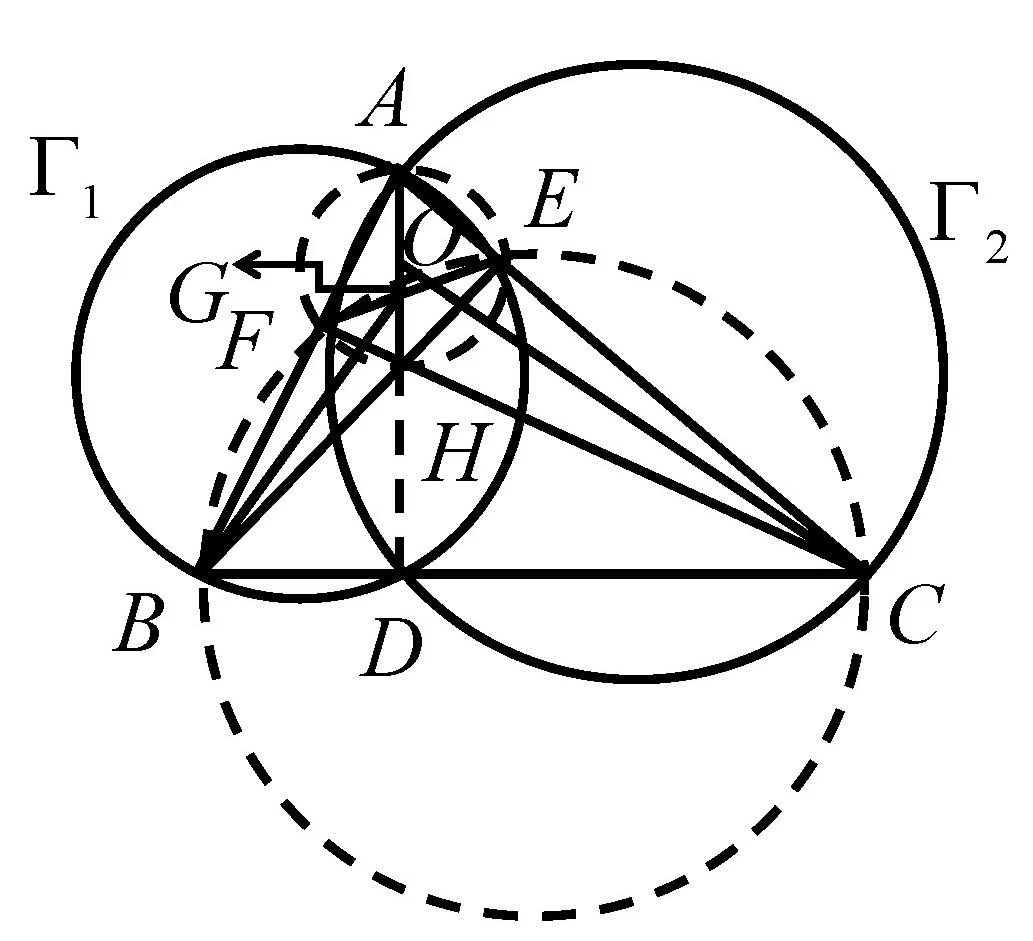
图3

由B、C、E、F四点共圆,知∠FBE=∠FCE,从而∠ABG=∠FCO．又CF⊥AB,所以∠GBC+∠OCB=∠GBC+∠FCO+∠FCB=∠GBC+∠ABG+∠FCB=∠FBC+∠FCB=90°,故CO⊥BG．

图4

注：上述证明过程整理自学生姜志城(2022年CMO金牌,进入IMO国家队)的解答．其关键在于利用面积方法和三角函数关系来巧妙处理线段关系,以及考查算两次原理的灵活运用．

3 类比推广

考虑到上述命题1和命题2中的ΔABC为锐角三角形,采用横向类比推理,不禁提出如下问题:

问题1 若将ΔABC为锐角三角形类比到直角三角形,则命题1和命题2中的结论是否成立?

分析：考虑ΔABC为直角三角形,根据图3和图4发现:

当锐角∠BAC逐步变大至直角时,点A、E、H、F所在的圆Γ4逐步退化成点A,于是CO与AC重合,BG与AB重合,而AB⊥AC,故有CO⊥BG;此时,线段LN与OH也随之退化成点A,如图5．

图5

问题2 若将ΔABC为锐角三角形类比到钝角三角形,则命题1和命题2中的结论是否依然成立?答案是肯定的,类比后的结论表述为下面命题3和命题4．

命题3 如图6,在钝角三角形ΔABC中,以AB为直径的圆Γ1与CA的延长线相交于另一点E,以AC为直径的圆Γ2与BA的延长线相交于另一点F,分别延长BE与CF交于点H,且AH交EF于G,O为ΔAEF的外心．证明:CO⊥BG．

图6

分析:考虑ΔABC为钝角三角形,AB、AC分别为圆Γ1、圆Γ2的直径,则有∠AFH=∠AEH=90°,故A、E、H、F四点共圆．于是在锐角三角形ΔBHC中,以HB为直径的外接圆Γ3与HC交于点F,以HC为直径的外接圆Γ4与HB交于点E,BF与CE交于点A,且AH交EF于G,O为ΔHEF的外心．这实质上等价于命题1,故CO⊥BG．

命题4 如图7,在钝角三角形ΔABC中,以AB为直径的圆Γ1与CA的延长线相交于点E,以AC为直径的圆Γ2与BA的延长线相交于点F,分别延长BE与CF交于点H,且AH交EF于点G．若O为ΔAEF的外心,BO与CE交于点L,延长CG分别交BO、BH于点M、N．证明:LN//OH．

图7

证明：考虑到AB、AC分别为Γ1、Γ2的直径,则AE⊥BH,AF⊥CH,故H为ΔABC的垂心,A、E、H、F四点共圆．设圆Γ1与圆Γ2交于另一点D,连接AD．因为AB、AC分别为圆Γ1、圆Γ2的直径,所以∠ADB=∠ADC=90°,所以AD⊥BC．注意到AF⊥FH,可知AH为ΔAEF外接圆Γ5的直径,故A、O、H三点共线．由于O为ΔAEF的外心,故由圆幂定理及余弦定理可得

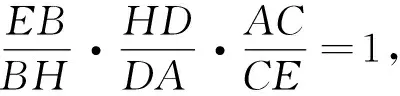
推广1 在非直角ΔABC中,以AB为直径的圆Γ1与直线AC相交于点E,以AC为直径的圆Γ2与直线AB相交于点F,直线BE与直线CF交于点H,且AH交EF于G,O为ΔAEF的外心,则CO⊥BG．

推广2 在非直角ΔABC中,以AB为直径的圆Γ1与直线AC相交于点E,以AC为直径的圆Γ2与直线AB相交于点F,直线BE与直线CF交于点H,且AH交EF于G．若O为ΔAEF的外心,直线BO交直线AC于点L,延长CG分别交直线BO、BE于点M、N,则(1)LN//OH;(2)AN、HL、EO三线共点．