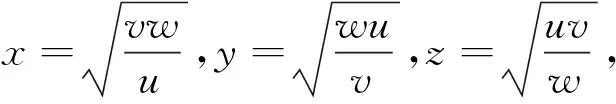一道数学竞赛不等式题的推广

山东省邹平双语学校 (256200) 姜坤崇

题目设x,y,z∈R+,且xy+yz+zx+xyz=4,证明:x+y+z≥xy+yz+zx.①

这是1996年越南数学奥林匹克竞赛的一道不等式试题是(参见文献[1]例3)本题对称优美、值得玩味,本文将这道竞赛题加以推广,得到如下一个新的不等式命题及若干推论.

命题设x,y,z∈R+,α∈R,且xy+yz+zx+xyz=4,则x2α+1+y2α+1+z2α+1≥xα+1yα+1+yα+1zα+1+zα+1xα+1.②

为证明不等式②,我们先证如下一个母不等式:已知a,b,c是正实数,则对任意实数x,y,z有

证明：将不等式③的左边减去右边可得

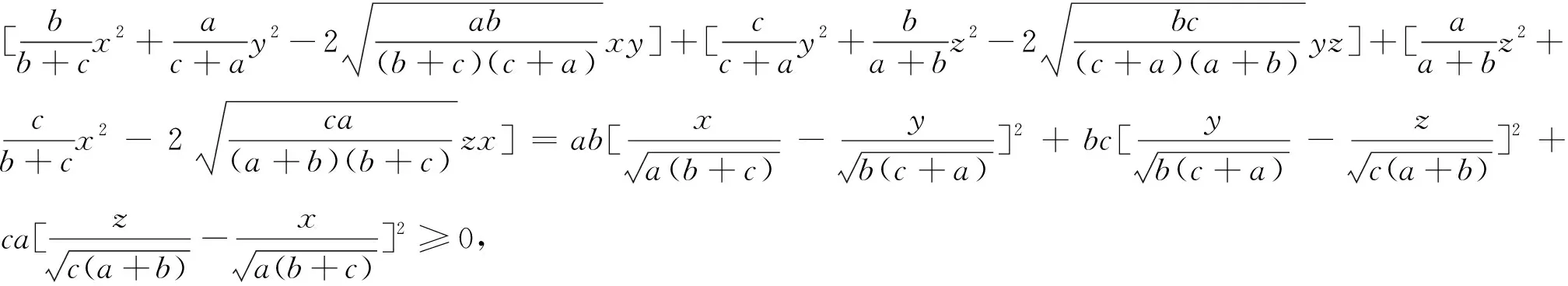
下面利用不等式③给出不等式②的证明.

显然,在不等式②中令α=0即得不等式①,因此不等式②是不等式①的一种推广.

推论1 设a,b,c>0,α∈R,且ab+bc+ca+2abc=1,则a2α+1+b2α+1+c2α+1≥2(aα+1bα+1+bα+1cα+1+cα+1aα+1).⑤

证明：令x=2a,y=2b,z=2c(a,b,c>0),代入xy+yz+zx+xyz=4即得ab+bc+ca+2abc=1,代入不等式②即得不等式⑤.

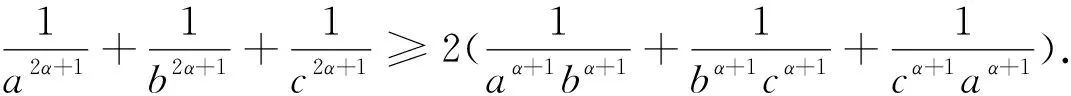
证明:在锐角ΔABC中有恒等式cos2A+cos2B+cos2C+2cosAcosBcosC=1,令a=cosA,b=cosB,c=cosC即为推论3中的条件式.将a=cosA,b=cosB,c=cosC代入⑦式即得⑧式.

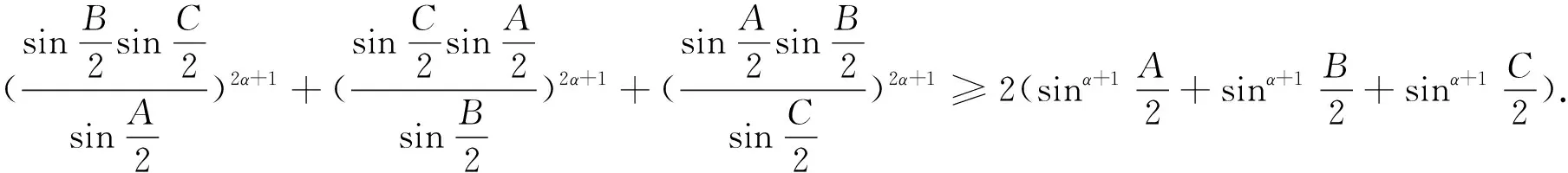
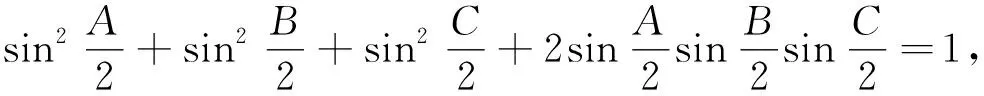
由于不等式②、④中的α是任意实数,所以可取α为一些具体的数值,可得许许多多的有等式条件限制与无条件限制的不等式.

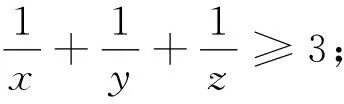
将此分式不等式化为整式不等式即为著名的舒尔不等式:

设a,b,c>0,则a3+b3+c3+3abc≥ab(a2+b2)+bc(b2+c2)+ca(c2+a2).

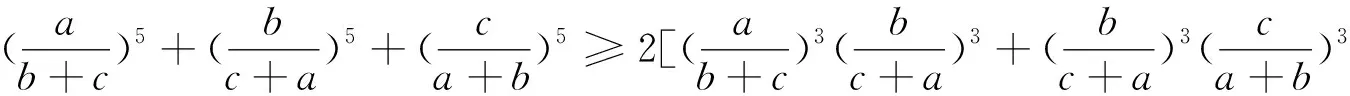
类似的,由不等式⑤,⑥,⑦,⑧也都可以得到许许多多的不等式,限于篇幅,这里不再给出.

文末,我们再给出文首竞赛题的两个变式问题:

题1 设x,y,z>0,且xy+yz+zx+xyz=4,证明:x+y+z+xyz≥4.

证明：由竞赛题的条件式可得xy+yz+zx=4-xyz,代入结论式x+y+z≥xy+yz+zx,即得x+y+z+xyz≥4,题1得证.