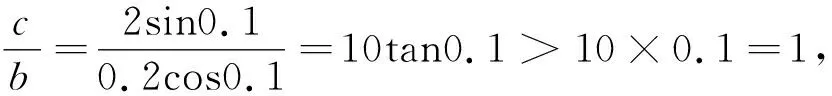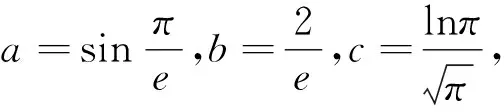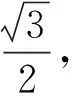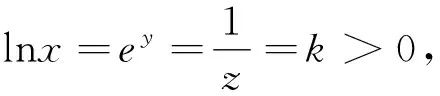观察结构特征 思悟内在本质——以破解比较大小问题为例

江苏省西亭高级中学 (226300) 瞿春波

江苏省南通市通州区教师发展中心 (226300) 瞿国华

从2023年2月的四省联考到各地模考,甚至近几年的高考中,时常在小题中看到比较大小的“影子”,它往往将幂(指数及对数)函数和三角函数、导数等联系在一起,这类问题交汇性强,难度较大.本文通过实例总结破解该问题的几种优化方法,供参考.

例1 (2023届四省2月联考)已知a,b,c满足a=log5(2b+3b),c=log3(5b-2b),则( ).

A．|a-c|≥|b-c|,|a-b|≥|b-c|

B. |a-c|≥|b-c|,|a-b|≤|b-c|

C. |a-c|≤|b-c|,|a-b|≥|b-c|

D. |a-c|≤|b-c|,|a-b|≤|b-c|

点评：由b的范围,从特殊情况入手,得a,b,c大小关系,再用二分法精确a,c的大致范围,从而去掉绝对值比大小.另外,用数形结合、极限、构造函数等方法也能破解此题.

例2 (2023届齐鲁名校高三二联)设a=sin0.2,b=0.2cos0.1,c=2sin0.1,则( ).

A.a

C．b

点评：作商后,三角化简,再利用三角函数线放缩为幂函数的值,从而比较大小.

A.a

C.b

A.a>b>cB.b>c>a

C.c>a>bD.b>a>c

例5 (2020届济南高三二模)已知实数x,y,z满足z·lnx=z·ey=1.则下列关系式中不成立的是( ).

A.x>y>zB.x>z>y

C.z>x>yD.z>y>x

点评：通过构造关于k(k>0)的三个函数,结合图象,比较函数值x,y,z的大小.

例6 (2022届T8高三一联)设a,b都为正数,aea+1+b

A．ab>eB.b>ea+1C．ab

点评：对条件变形,观察结构特征,构造函数f(x)=xlnx并确定单调性,从而得到自变量值的大小关系.

A．b>a>cB．b>c>a

C．a>b>cD．c>a>b

点评：通过两次构造函数,先比较g(x)函数值大小,再比较f(x)自变量值大小.

A.a

C.c

例10 (2023届绵阳高三二诊理科卷)设x=e0.03,y=1.032,z=ln(e0.6+e0.4),则( ).

A.z>y>xB.y>x>z

C.x>z>yD.z>x>y

总之,比较大小问题,形式多样,方法灵活,但离不开基本知识和方法,掌握此类问题的通性通法,熟练变形技巧与破解策略,从而让数学核心素养落地生根.