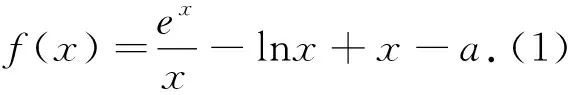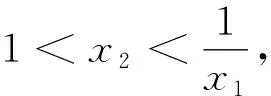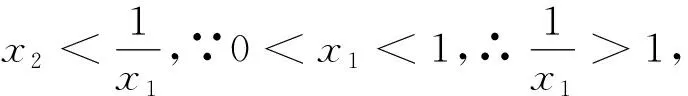比较大小型高考试题的解法探究
山东省德州市陵城区第一中学 (253500) 侯怀有
比较大小型试题是高考试题的常客,也是同学们解题的难点,本文从三方面对这类问题进行精析,帮助同学们掌握这类问题的解法.
一、同构构造
同构构造针对的是条件给出一个等式或不等式的问题,将等式或不等式的两边整理为结构一致的代数式,从中归纳总结抽象出母函数,再利用函数的单调性比较大小.在整理时,先将两个变量分别置于式子的两边,若结构相同,即可构造函数;若结构不相同,再将其中一个式子通过放缩法转化为结构完全相同的式子.
例1 (2020新课标Ⅰ)若2a+log2a=4b+2log4b,则( ).
A.a>2bB.a<2bC.a>b2D.a 构造精析:观察所给的等式,两个变量位于等号的两边,两边结构类似,都是幂和对数的和;但又不完全相同,等号前面的底数都是2,而后面都是4.能不能把底数4化为底数2呢?可以,根据指数和对数的性质可得4b+2log4b=22b+log2b,但是结构还是不完全相同,再将22b+log2b放缩一下22b+log2b<22b+log22b,就得到了结构完全相同的式子2a+log2a<22b+log22b,再构造函数就水到渠成了. 例2 (2020新课标Ⅱ)若2x﹣2y<3-x-3-y,则( ). A.ln(y-x+1)>0 B.ln(y-x+1)<0 C.ln|x-y|>0 D.ln|x-y|<0 构造精析:由于变量x、y没有位于式子两边,先移项将其变形为2x-3-x<2y-3-y,此时两边结构完全相同,可构造函数f(x)=2x-3-x进行求解即可. 解:由2x-2y<3-x-3-y,可得2x-3-x<2y-3-y,令f(x)=2x-3-x,则f(x)在R上单调递增,且f(x) 比较三个数大小的问题难易不一,对于比较简单的问题,通过直接运用函数的单调性和中间值即可确定大小,而较难的问题需要先作差,然后再根据式子中数与数之间的联系,选择合适的变量,构造恰当的函数. A.a C.c A.a C.b 此类问题与函数的零点有关,根据两个零点的取值范围以及两零点之间关系将双变量式子转化为单变量式子,然后构造函数进行解题 “授之以鱼,不如授之以渔”.通过以上三个方面的精析,引导同学们从已知代数式或已知数的结构特征出发,细心观察,大胆猜想,通过构造函数函数并利用其单调性解决问题.另外,构造函数体现了分类讨论思想,转化化归思想,函数思想等数学思想方法的具体运用,有效地锻炼同学们的观察能力,直观想象能力,抽象概括能力,推理论证能力,使同学们在解题过程中,不断经历感知、想象、认同、抽象、重构等思维过程,而这正是数学新课程核心素养不可或缺的重要内容.
二、作差构造
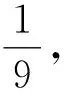
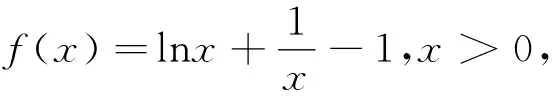
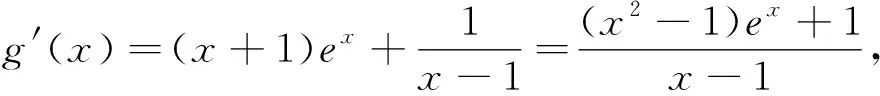


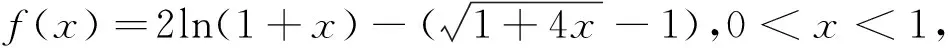
三、根据零点的关系构造