例谈利用齐次化求一类分式递归数列的通项

山西省太原市第三实验中学校 (030031) 董立伟

人教A版《普通高中教科书数学选择性必修第二册》(2020年5月第1版)(以下简称“选修二”)第四章《数列》部分出现了许多由一次分式形式的递推关系猜想通项公式的数列问题. 这类问题本身并不难解,但学生们更想知道的是如何通过严格的推理得到这类数列的通项公式. 对分式递归数列,我们熟知的求通项的解法是不动点法. 这种方法确实巧妙,但是学生们也只能套用,很难理解其深刻的数学内涵. 事实上,利用齐次化的方法可以得到求解此类数列通项公式的一种初等解法.

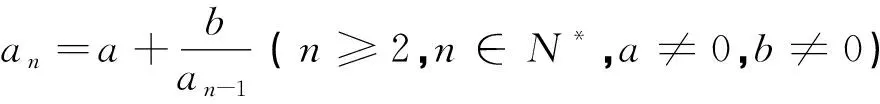
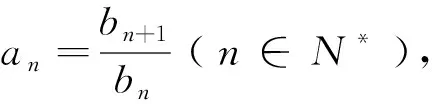
第三步(构造).利用待定系数法构造新的等差或等比数列求数列{bn}的通项公式;

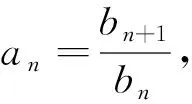
以下用两个例子来阐述该类型问题的解法.

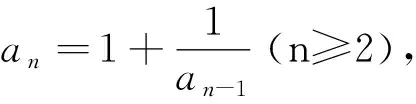
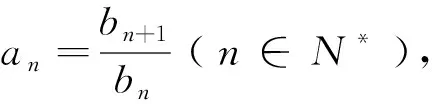
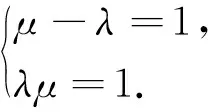
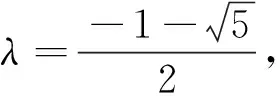
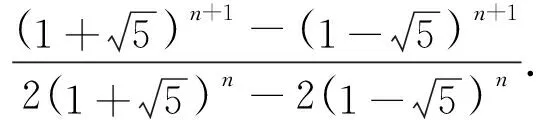
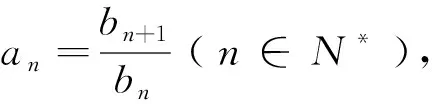
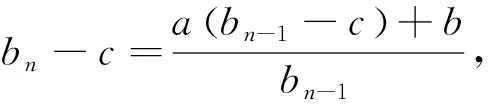
以下用两个例子描述该类型问题求解过程.

例3 (选修二第48页例3改编)已知数列{an}满足a1=0,2an+1-anan+1=1(n∈N*),求数列{an}的通项公式.

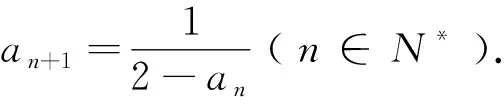
例4 (选修二第51页习题4.4第3题改编)已知数列{an}满足a1=1,4an+1-anan+1+2an=9(n∈N*),求数列{an}的通项公式.

结语：利用齐次化,我们将一次分式形式的递推关系转化为二阶线性递推关系,进而可以利用待定系数法构造新的等差或等比数列,求得其通项公式,从而得到此类问题的一种更易为高中生接受的初等解法.