基于APOS理论的函数单调性概念教学设计

江西省南昌县莲塘第一中学 (330200) 魏 红

一、APOS的概念教学阶段

杜宾斯基认为,学习者在学习数学概念时要进行心理建构,这个建构过程需经历活动、过程、对象和图式4个阶段.“活动阶段”是指将具有内隐性的数学概念通过一系列外显的探究活动来获得.在函数单调性概念中,可借助几何画板观察图像上动点的变化规律,并由此得到概念的雏形.“过程阶段” 是对外显数学活动的进一步思考过程.当学生经过多次重复活动并对其熟悉后,便会在头脑中抽象出概念的本质特征.“对象阶段”是给抽象出的本质特征赋予形式化的定义和符号,使其成为一个具体的对象.“图式阶段”是与其它概念建立联系,形成知识的综合图式,并把这个图式纳入自身的认知结构中,与已有的知识建立新的实质性联系.

二、“函数单调性概念”教学四阶段的设计

1.活动阶段

阶段目标:直观感知函数图像在某区间上的变化趋势.

教师:引导学生说出函数f(x)=x+1,f(x)=x2,f(x)=x-1的变化趋势.

学生:不难得出f(x)=x+1在R上呈上升趋势,如图1;f(x)=x2在(-∞,0)上呈下降趋势,在(0,+∞)上呈上升趋势,如图2;f(x)=x-1在(-∞,0)上呈下降趋势,在(0,+∞)上呈下降趋势,如图3.

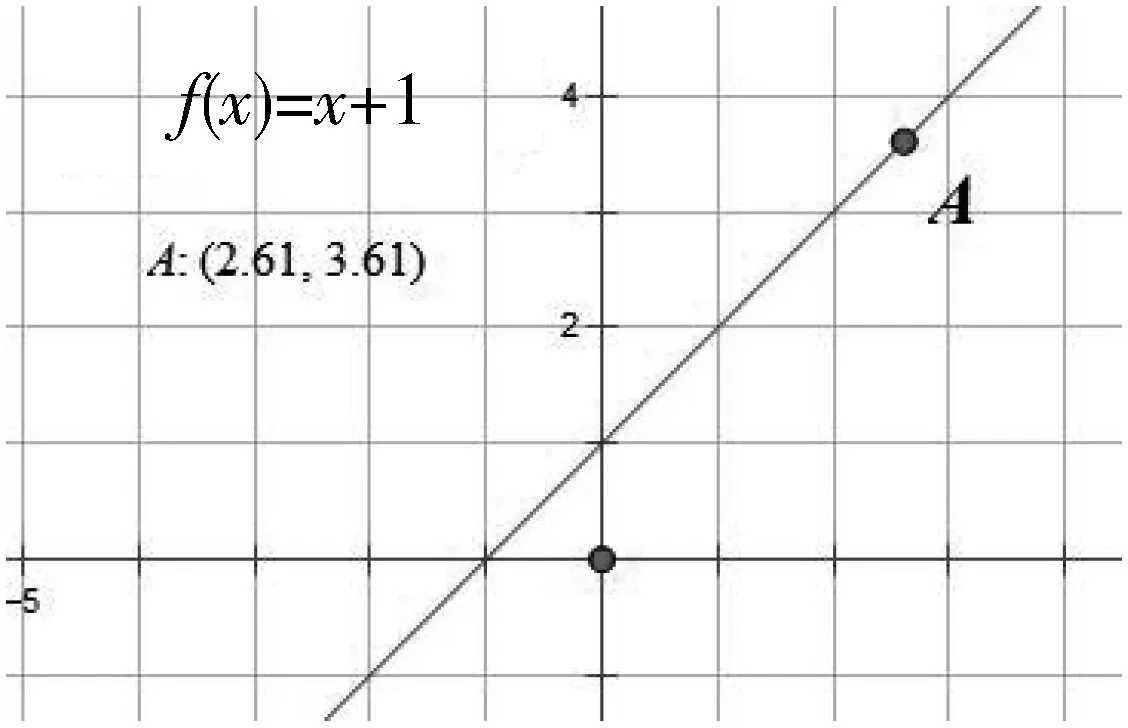
图1

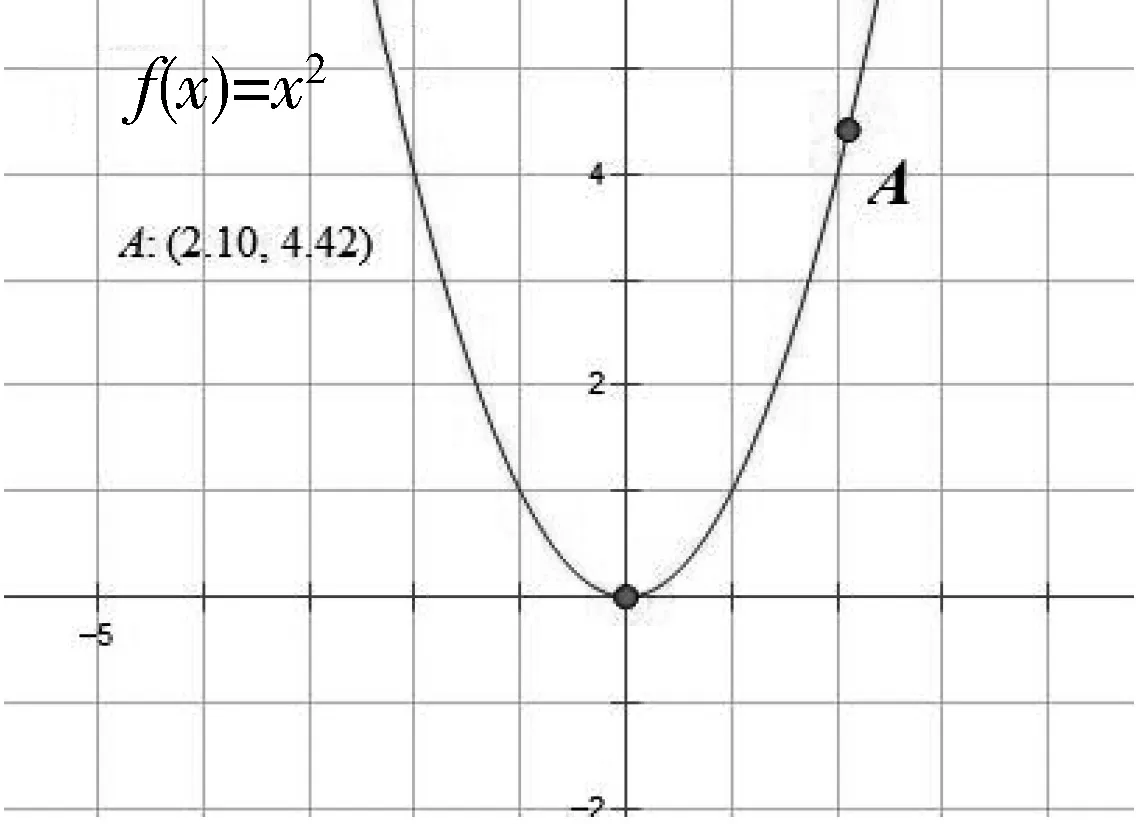
图2

图3

教师:函数图像是满足某种规律的点集,所以,我们可以将函数图像变化趋势这个问题转化到图像上点的变化规律.引导学生思考用点的横纵坐标变化关系来描述函数f(x)图像变化趋势,并借助几何画板软件动态验证函数图像上动点A从左到右拖动过程中的坐标变化关系.

学生:通过观察点A沿着图像拖动过程中点A坐标的变化.认识到如果函数图像在区间D上呈上升(下降)趋势,则在区间D内,从左往右看,y随x增大而增大(减小),从右往左看y随x减小而减小(增大).

教师:提出增减函数的初步认识.如果在区间D上y随x增大而增大,或y随x减小而减小,则称函数f(x)在区间D为增函数,反之,为减函数.函数的这种性质称之为“单调性”,D为函数f(x)的单调增(减)区间.

2.过程阶段

阶段目标:从图形上,我们已感知到到增(减)函数y随x的增大而增大(y随x增大而减小),那么怎么理解y随x的增大而增大(减小)呢?学生的思维还不够抽象,在某区间上有限对变量的变化关系都不能反映增函数的本质,通过问题引发学生的思考并意识到x1,x2的任意性,从而进一步引出函数单调性的定义,这是本节课的重难点.

教师:以函数f(x)=x2为例,取x=1,2,3,4,5…相应地,y=1,4,9,16,25…这样能不能说函数在(0,+∞)上y随x的增大而增大?

学生:不能,因为只取了自变量在(0,+∞)一些特殊值时,函数值y随x的增大而增大,这不代表所有,不能说明自变量取在(0,+∞)上其他值时也符合这个规律.

教师:x和y都属于无限集合,我们不能将有限列举得到的函数变化规律推广到自变量在无限区间上,实际上函数图像上定点不能无限列举,那我们可以考虑从函数图像上取动,那么取几个动点呢?

学生:前面取一个动点,要规定拖动动点的顺序,也就是控制动点横坐标变化前提下,观察动点的纵坐标变化情况.实际上,可以在函数图像取两个动点,因为两个动点可以比较x和y的增大或减小,从而刻画它们之间的变化关系.

教师:函数f(x)=x+1,f(x)=x2,f(x)=x-1的任取点A和B,保证点B在点A右边(或左边)的前提下,拖动A、B两点,并用几何画板度量点A的坐标变化.

学生:对于函数f(x)=x+1,如果点B在点A右边,即点B横坐标大于点A横坐标前提下,点B纵坐标会一直大于点A纵坐标,如图4.

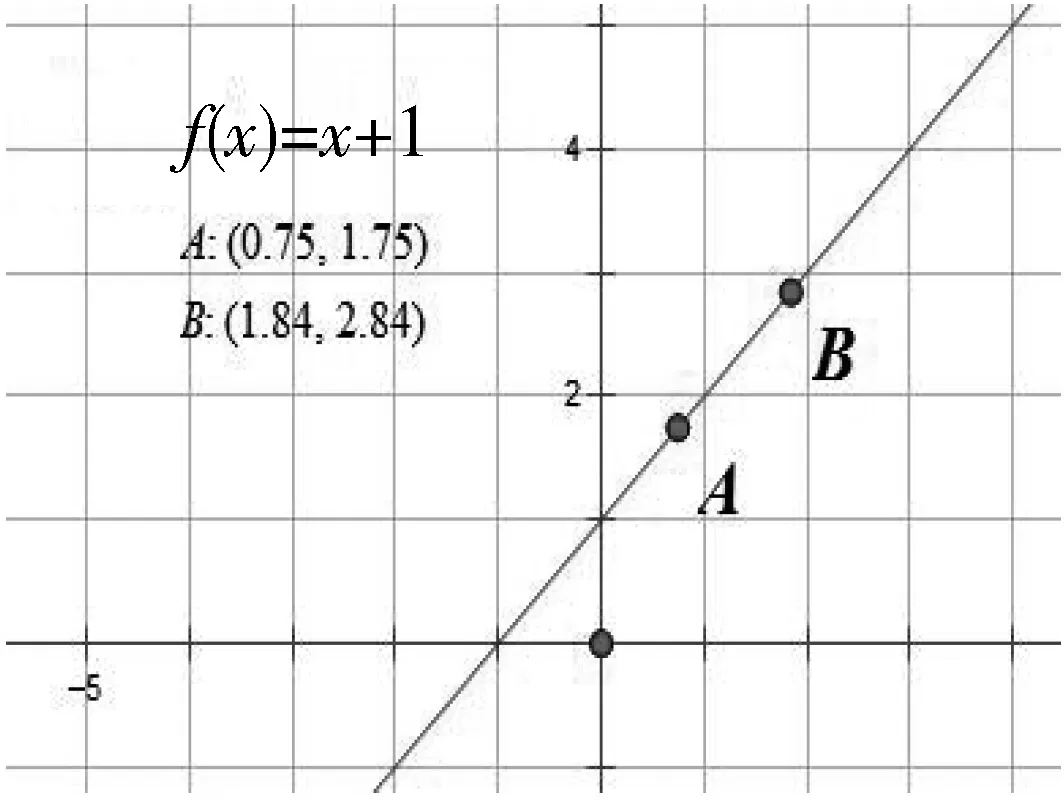
图4

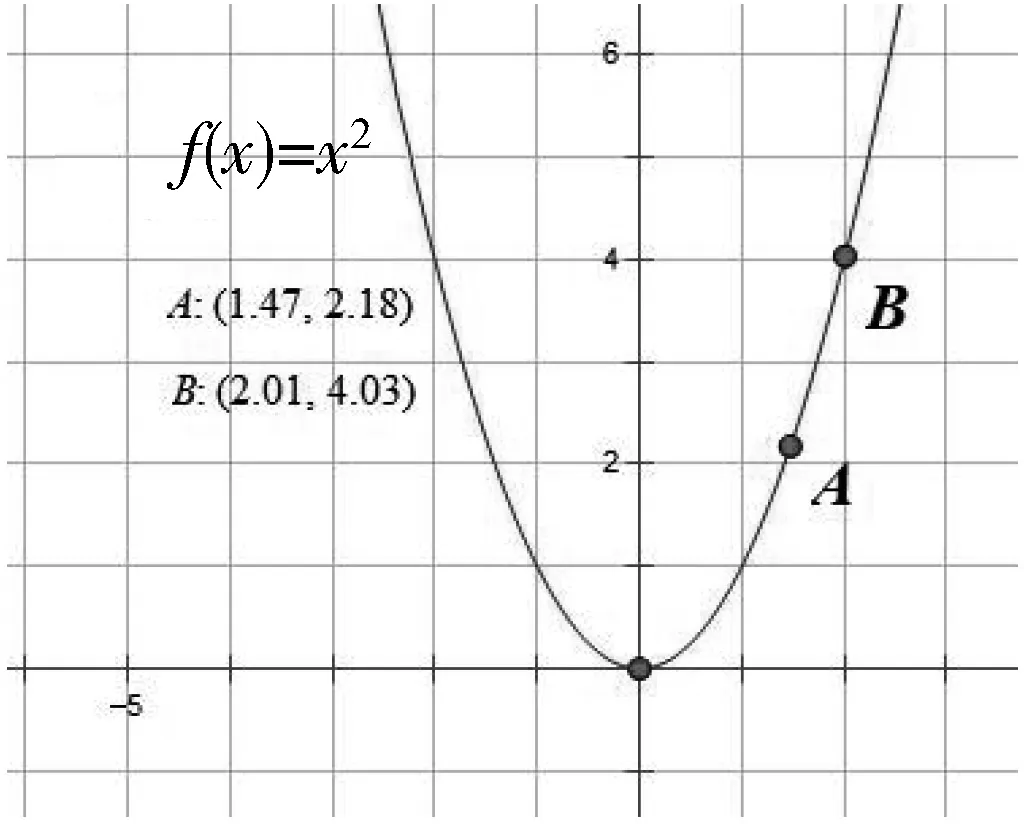
图5

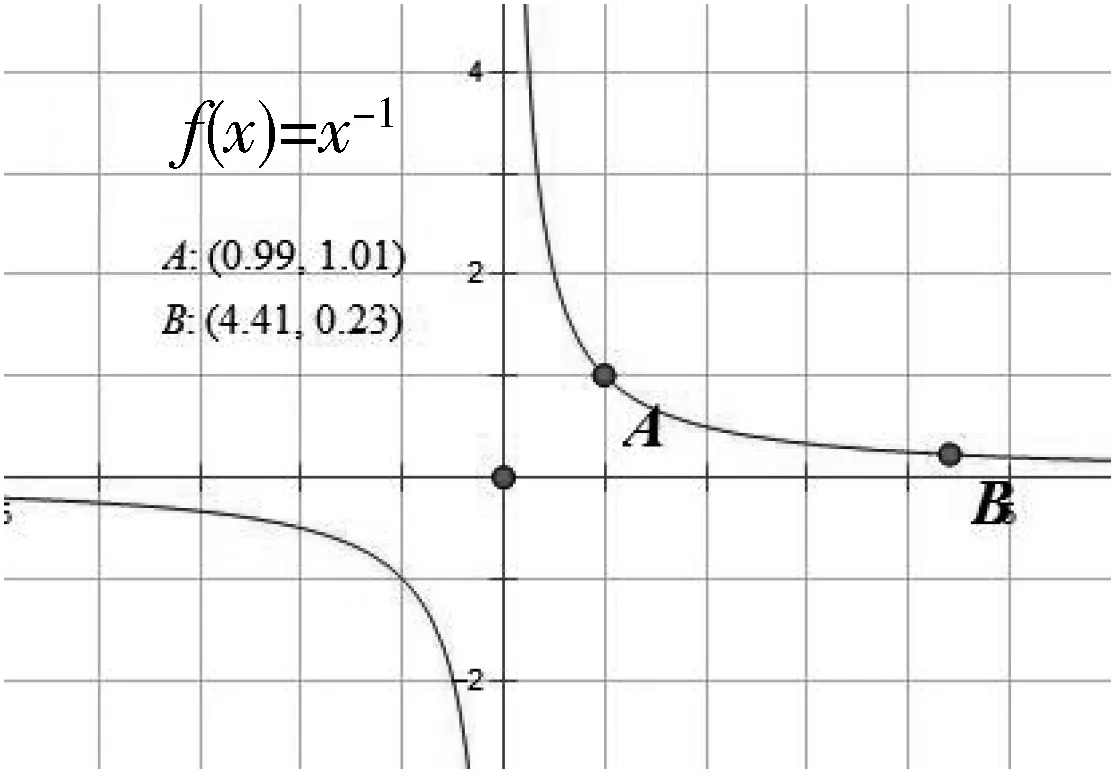
图6

教师:对于函数f(x)=x2,f(x)=x-1,有同样的结论吗?

学生:要注意单调区间,要控制点A和B在y轴同侧,即同在右边或左边.

教师:用几何画板动态展示点A和B在y轴异侧情况下,如图7,8.

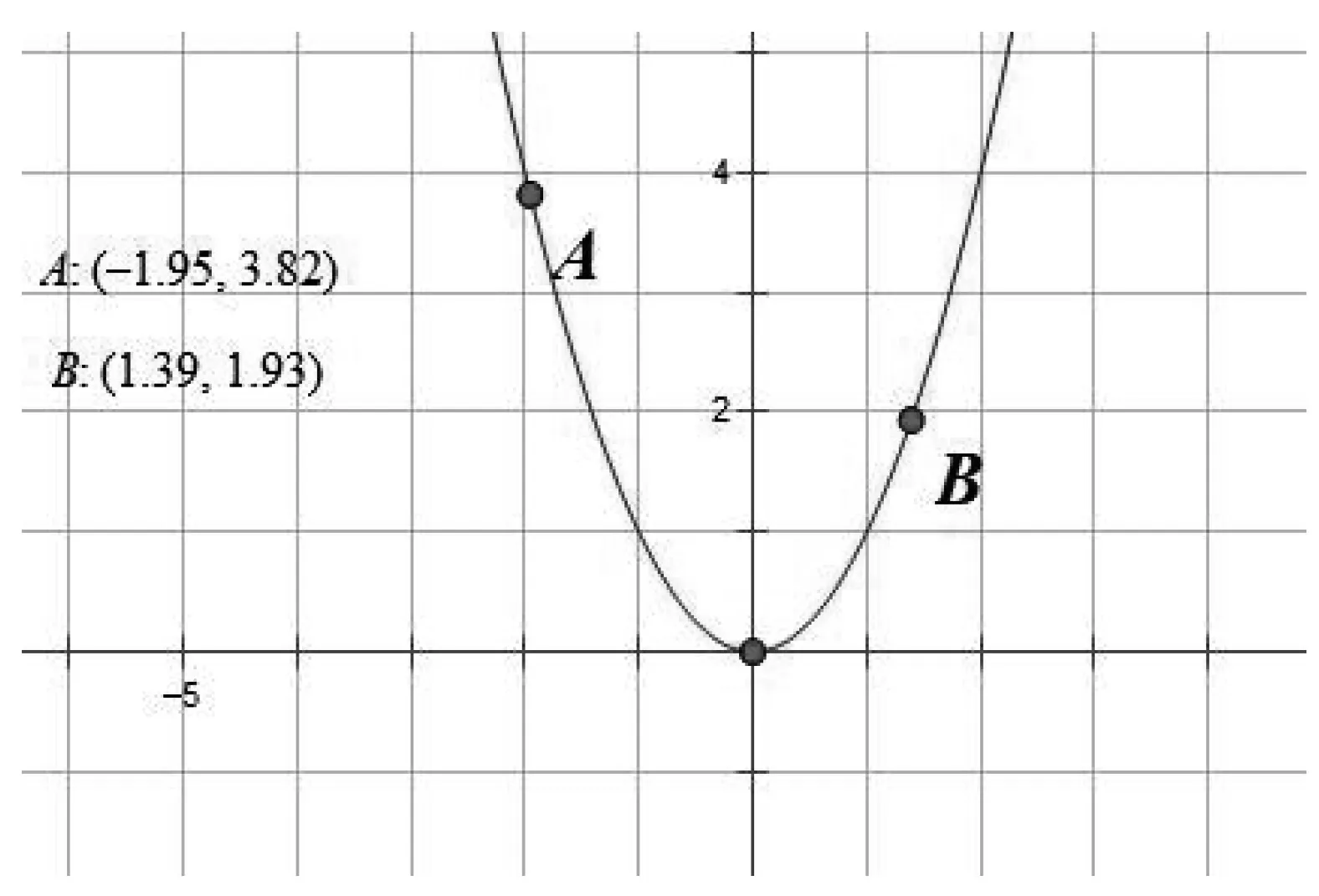
图7

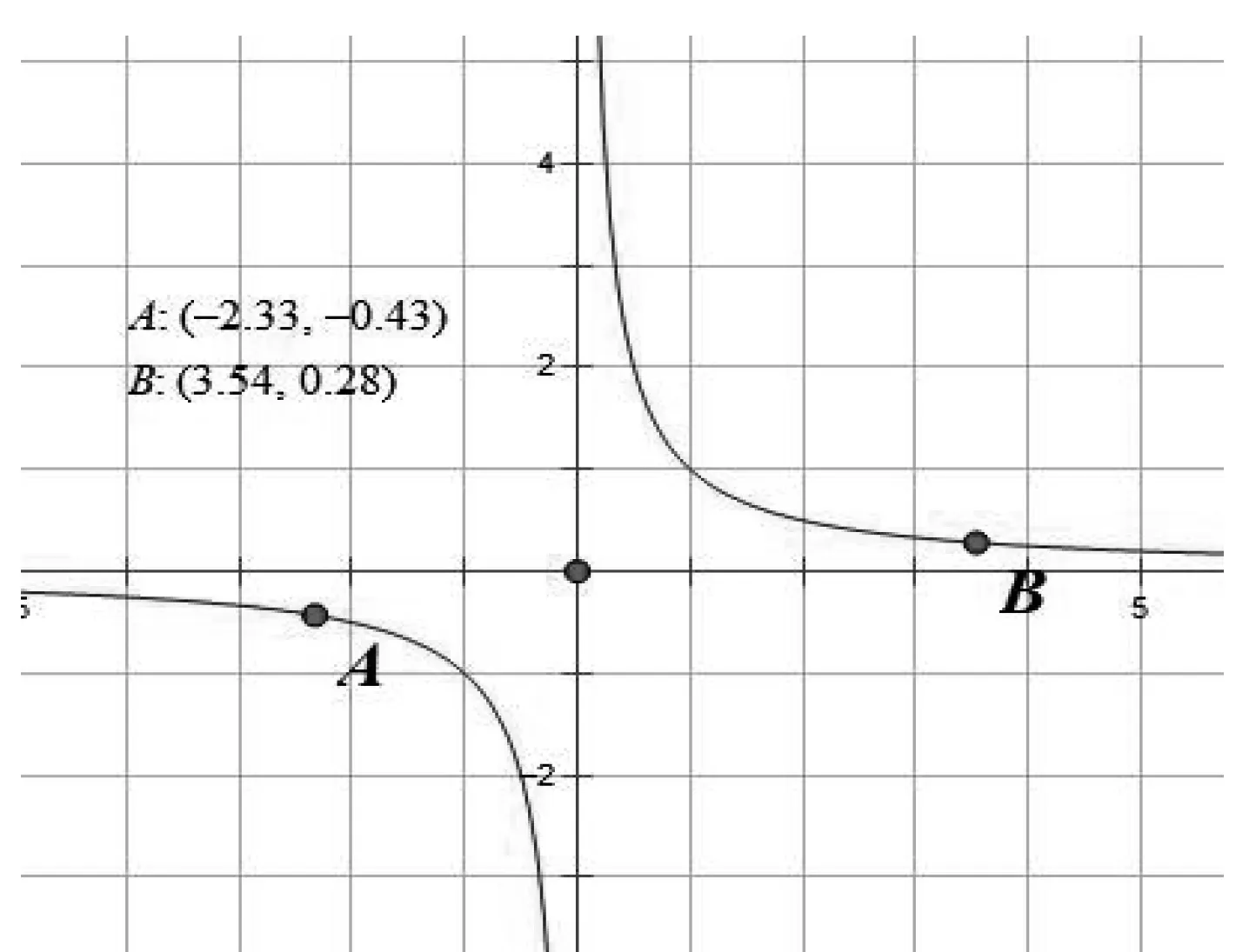
图8

学生:得不到同样结论,意识到函数单调区间是定义域的子集,函数在区间具有单调性,不能说明在整个函数定义域也具有单调性.函数单调性只是函数的局部性质.如不能说f(x)=x-1在(-∞,0)∪(0,+∞)上是减函数.

3.对象阶段

阶段目标:用数学语言描述“增函数”与“减函数”.

教师:前面我们说,在区间D上y随x增大而增大,或y随x减小而减小,则称函数f(x)在区间D为增函数,反之,为减函数.而y随x增大而增大,我们可以用数学式子的不等关系替换.

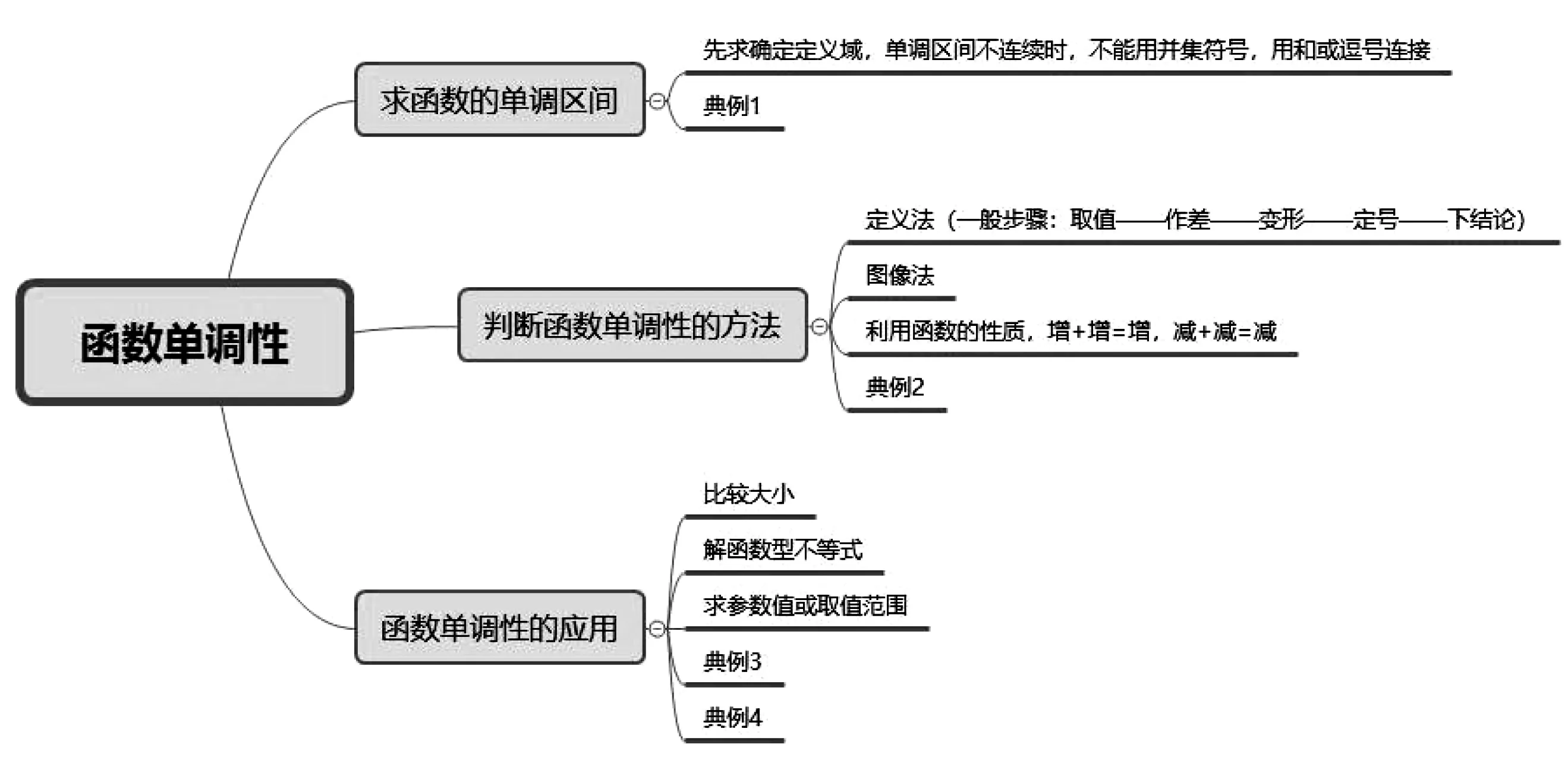
4.图式阶段

阶段目标:函数单调性的知识网络结构图:

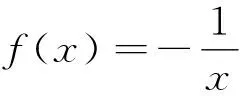
变式1 将例1中的函数改成

变式2 将例1中的函数改成f(x)=-x2+2|x|+3.

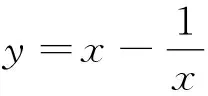
小结:在公共区间内,若f(x),g(x)都有单调性,则有:

f(x)是增函数g(x)是增函数f(x)+g(x)是增函数f(x)是增函数g(x)是减函数f(x)-g(x)是增函数f(x)是减函数g(x)是增函数f(x)-g(x)是减函数f(x)是减函数g(x)是减函数f(x)+g(x)是减函数

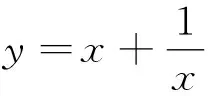
典例3 若函数f(x)=-x2-2(a+1)+3在区间(-∞,3]上是增函数,求实数a的取值范围.

变式将上例函数单调性改成在区间(1,2)上是单调函数,求实数a的取值范围.

典例4 已知函数y=f(x)在(-∞,+∞)上是增函数,且f(2x-3)>f(5x-6),求实数x的取值范围.

变式将上面函数定义在(0,+∞)上是增函数,求实数x的取值范围.

三、进一步的思考

本教学设计以“活动——过程——对象——图式”4个阶段展开,环环相扣,循序渐进.在“活动”阶段,教师创设问题情境的目的主要在于让学生理解函数单调性概念的直观背景和概念间的关系,感知函数变量之间的相互依赖关系.在该阶段中获得了初步感觉印象的基础上,“过程”阶段需对其不断进行完善,引导学生学生在操作中反思反思,又在思考中操作,这样得到“函数单调性”概念的认识,并且进入“对象”阶段.第三阶段是对以上2个阶段抽象出的概念所特有的性质赋予形式话的定义及符号,使其达到精致化,成为一个具体的对象.图式阶段是将概念作为一个已知对象应用到它生存的土壤或背景中,促进概念的内化.

简而言之,APOS理论作为一种数学概念学习论,为我们提供的循环上升的连续的阶段,牵引并支持着学生在自己的经验和数学本质之间不断对话,在连续性地回顾与反思过程中提升、扩充学生的经验认识,丰富、深化对数学本质的理解.