一题一课:高三复习课的教学设计与思考

吴玉珠 刘建国

摘 要：通过一道模考试题的图形绘制以及图形分析，在一课一题的教学活动中探究解题，以绘制图形为基础，思维导图分析为主线，建构学生解决问题的基本路径，在复习过程中将知识点进行串并，达到以点带面，以试题解答串联知识点的复习，培养学生的数学学科关键能力.

关键词：一题一课；新高考；教学设计；图形绘制；思维导图

“一题一课”是指教师通过对一道例题或一段材料的深入研究，充分挖掘其内在的学习线索，并科学、合理、有序地组织学生进行相关的教学探索活动.采用一题一课的教学模式并非以问题求解为目的，而是教师应站在更高的层次引领学生探索，帮助学生由一道典型问题的解决打开学生的思维，能够以点带面的复习，串联起相应的知识点，了解考点呈现的形式，真正意义上培养学生的学科关键能力.

当前新高考背景下，从试题特点上看，试题并没有给出相应的图形，这无疑对学生的作图能力有了更高的要求，同时给试题增加了一定的难度.教师在试卷讲评时，应注重学生的作图能力以及对图形的分析能力.能够准确地做出图形，并在图形上分析问题是解决问题的关键，笔者在近期的试卷讲评课上甄选一道例题进行一题一课教学，从深度与广度上分别对问题进行剖析，将复习目标真正落实到实处.

1 例题呈现

例1 （南京市2023届高三年级学情调研）在平面四边形ABCD中，∠ABD=45°，AB=6，AD=32.对角线AC与BD交于点E，且AE=EC，DE=2BE.

（1） 求BD的长；

（2） 求cos∠ADC的值.

注：本题以四边形为载体，主要考查学生余弦定理，其中问题（1）是问题（2）的一个铺垫，在（1）中对问题进行求解是为了帮助学生更好地确定图形，因此在解决问题时，帮助学生建构图形，进而培养学生分析问题和解决问题的能力.

2 易错分析

例题中学生存在的错误主要有三个方面：首先是学生对图形的绘制出现错误，不会画图或画图不准确导致后续的解答无法进行；其次是问题分析不准确，思维能力欠缺，主要体现在思维品质不具备灵活性，聯系性，创造性，同时思维方法上没有条理性，无根无据的思考不具有连贯性，导致对于问题的把握不够准确；最后是数学运算方面出现错误，不会算，运算出错等问题层出不穷.

由于例题中并没有给出相应的图形，首先要将抽象的题设条件以图形的方式展示出来，因此解决此类问题必须先画出相应的图形，很多学生在作图时出现了不同程度的错误，究其根本原因在于对题中的度量关系，线段之间的比例关系没有统筹把握，导致所作的图形出现各种问题，笔者认为，在解决此类问题过程中，在实际作图解决问题时应注重数形结合的思想的引领，以图形的直观性把握问题的核心，通过数与量之间的数学运算，逻辑推理得出相应的结果.此外在作图与分析问题时应兼顾对应思想，这种对应是指条件与图形的一一对应，数学知识与方法的思维逻辑对应，已知条件与未知量之间的对应转化.

3 图形绘制

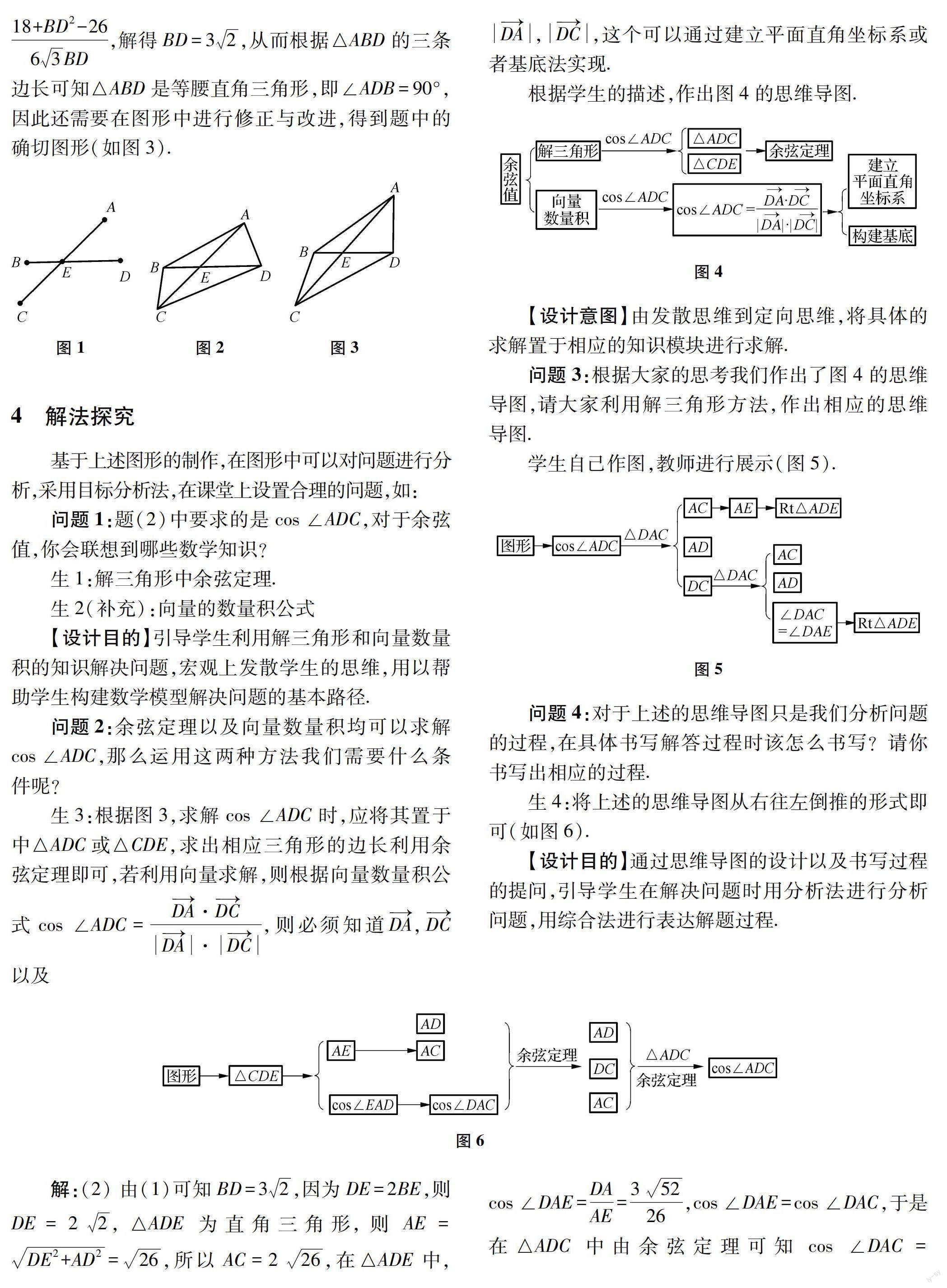
根据题中的条件，首先作出对角线AC与BD，根据条件且AE=EC，DE=2BE，确定点E的位置（如图1），再通过作∠ABD=45°，以通过线段AC绕着点E旋转，使得∠ABD=45°即可，随后连接AD，BC，CD，AB，即可得到题设条件中的图形（如图2）.

6 题后反思

教师应注重引导学生对所研究问题图形的绘制.新高考背景下，试题仅仅以文字语言形式呈现（解三角形、圆锥曲线、导数等），其抽象性使得问题的难度加大，隐性的考查了学生的作图能力.图形是思维活动的关键，只有将图形准确地作出，才能更好地将问题的本质直观化，反映问题的本质所在^［1］.教师在复习过程中应引导学生对试题中图形的绘制，充分的把握条件与图形的对应，未知量在图形中的呈现，在条件与图形对应时不断地对图形进行调整与修正，最终呈现完整的图形，为分析问题与解决问题做好铺垫.

一题一课注重对例题的深度挖掘.一题一课不是仅仅就题论题，而是注重“借题发挥”，教师应站在更高的层次上对问题进行深度挖掘，帮助学生从例题中复习相应的数学知识，引导学生对问题进行分析，注重考点以何种形式呈现（长度、面积，正余弦等），如何能够迅速地抓住问题的核心，以及对数学知识的应用.此外注重引导学生将数学知识进行串并，使得各个模块的数学知识进行整合，帮助学生能够整体性的把握知识的应用与理解，做到由一题会一类题，由一题复习多个知识模块以及其内在联系，真正意义上达到以点带面的复习效果.

问题探究注重思维导图的应用.思维导图的构建能够帮助学生对所思考的问题进行全方位的分析，在一定程度上呈现学生所研究问题的思维障碍，同时也可以帮助学生在思考问题时富有创造性的思考.通过思维导图的层次性能够更好地加深学生对问题的理解与认识，理清解决问题的障碍所在，将其可视化展示^［3］.如在文中例题^［1］，通过思维导图的方式，可以很便捷地呈现所有解决的问题在于CD，也就是问题的障碍所在，进而层层分解的形式帮助学学生克服问题的思维障碍；此外通过对cos∠ADC进行创造性的思考，得出了向量数量积的基底法与建立平面直角坐标系.由于选择的基底方式与建系方式不同，得到的解题过程就会不同，自然而然地呈现了一题多解的形式.

参考文献：

［1］ 刘建国，马一新.图象视角下导数问题的解题思路与命题策略［J］.数学通讯，2022（13）：42-45.

［2］ 王健.思维导图在高中数学教学中的应用［J］.中学数学月刊，2022（3）：25-27+54.