基于尝试教学理论的高中数学教学模式探究
王跃

摘 要:随着教学体制的不断改革与完善,新课改的理念应运而生,高中阶段的数学教学逐渐演化成更加丰富、更加多元的教学模式.在制定教学方案、实施课堂教学的過程中,教师需要掌握学生的实际情况,以激发学生学习欲望、培养学生学习思维方式、提高学生学习技能为首要目标,获得更为优质的课堂教学模式.尝试教学模式以引导学生的尝试活动为重点,可以通过有效问题的设计引导学生进行尝试性的思考,通过课堂合作小组的建立促进学生进行尝试性的课堂交流,并结合课堂猜想活动推动学生的尝试性思考,从课堂教学设计上推动课堂的高效运转.
关键词:高中数学;尝试教学理论;课堂实践;教学策略
尝试教学理论来源于我国著名学者邱学华教授,其创作的目的和概念在于对“尝试”二字的理解和贯彻.“尝”可以定义为辨别、探究的意思,在于获得对问题难易程度的基本认知;而“试”则是将针对所辨认的问题的解决方式预想付诸实践,通过实践来获得真知[1].因此,“尝试”更多的是一种审视问题、预设方案、实践方案的探究性过程,基于尝试教学理论的课堂教学能够强化学生的探究性思维、促进学生的探究型活动,让学生成为知识的探索者与挖掘者,从而提高学生在教学过程中的主体地位,使得学生获得更加丰富、更加直观的教学体验[2].
1 设计有效问题,引导学生尝试思考
所谓尝试教学,即要推动学生在课堂中的尝试性思维以及常识性活动,让学生成为课堂教学的潜在主导者[3].以往数学教学中,学生都是跟随教师的主导,被动接收已经成型的知识,缺乏对知识的进阶思考和挖掘.在尝试教学理论的教学活动之下,教师要善于设计科学、有效的数学问题,给予学生思考的机会和空间,让学生在问题的引导下尝试性地去思考、去解决,从而完整地经历知识形成的过程,对知识也能有一个更加深刻的认识,有效提高对知识的理解,同时获得一定的数学学习能力.
2 发挥小组合作模式,促进学生尝试交流
在高中课堂,学生人数比较多,掌握的知识量以及对问题的理解能力也各不相同,同时学生之间的合作交流也很缺乏,难以通过开放的课堂掌握更多有效的学习方法[4].因此,尝试教学理论可以以推动学生常识性交流、尝试性合作为目的建立课堂合作小组,让学生在教师的指导下与组内的成员进行交流,促进思维的碰撞,通过合作的形式获得更加全面、更加完整的知识结构.
3 激发学生课堂猜想,推动学生尝试思考
尝试教学理论需要提供给学生尝试的机会以及尝试的平台,因此教师要善于在课堂中巧设疑问,引导学生进行合理的猜想并跟进针对猜想的验证过程,通过猜想去尝试思考问题、解决问题,以此获得更加完整的学习体验.值得注意的是,教师要考虑到课堂教学内容的难易程度以及课堂教学的时间限制,针对猜想的问题设置要贴合教学主题,同时能够让学生在有限的时间内获得合理的猜想并验证,寻求课堂教学的效率最大化[5].
4 基于尝试教学理论的高中数学教学案例
接下来笔者以人教版高中数学必修第二册“平面向量的基本定理”为例简述如何在尝试教学理论下开展高中数学有效教学,从教学模式上寻求学生学习质量与学习思维的双赢.
4.1 教学分析
平面向量的基本定理是基于向量的线性运算展开的,它是从向量分解的角度考查平面向量之间关系的衍生产物,在本质上是对平面向量的分解运算,在一定程度上构建了平面向量体系的理论基础,在整个向量学习乃至整个高中学习过程中十分重要.平面向量的基本定理中“基本”一词彰显了它在向量学习中的奠基性作用,同时它体现了向量的线性构造,揭示了两个向量在平面中的位置关系以及线性相关性,帮助学生建立了低维度向量认知,为以后学生分析高维度向量关系提供了线索,因此教师要考虑到该定理学习的重要性,结合尝试教学理论帮助学生开展尝试学习,体会学习过程中的数学概念以及数学思想.
4.2 教学目标
(1) 让学生掌握平面向量的基本定理,并能够合理利用这些定理去解决实际问题,训练自身知识应用的能力;
(2) 类比平面向量的数乘运算,帮助学生理解平面向量基本定理中关于两个向量之间未知关系与数量关系的本质,实现对平面向量基本定理的直观化认识;
(3) 让学生经历假设猜想、证明猜想以及总结结论的数学学习过程,掌握概念、定理等基础数学知识的学习方法.
4.3 教学重难点
教学重点是平面向量的基本定理及其本质,并将其运用到实际解题过程中去;教学难点是对平面向量基本定理本质的分析和抽象化理解.
4.4 教学环节
环节一:创设情境,引入主体
教师:通过之前对平面向量基本知识的学习,大家已经掌握了相关的向量知识并具备在向量空间的概念下思考问题的能力,那么接下来请大家以小组为单位,思考并交流以下几个问题:
问题1:如果向量a可以用向量b表示,那么它们之间存在什么关系?
学生交流:如果向量a可以用向量b表示,那么它们一定处于同一个平面内且共线.
问题2:如果向量a和向量b位于同一平面但不共线,那将其利用三角形法则进行相加得到的向量c=λa+μb是否位于该平面内呢?
学生交流:如果向量a和向量b位于同一平面且不共线,形如c=λa+μb的向量也位于向量a和向量b的平面内.
教师:很好,那请大家逆向思考以下问题:如果向量a和向量b位于同一平面但不共线,平面内任一向量c是否可以用向量a和向量b来表示呢?而这个问题也就是我们今天所要学习的内容“平面向量的基本定理”的本质.
【设计意图】通过小组合作与问题设计的形式推动学生针对教学内容进行尝试性的思考和交流,让教学课堂更加丰富、开放,为学生的知识获取过程增添乐趣,有利于促进学生的高效学习.
环节二:数形结合,假设猜想
教师:既然大家对平面向量的位置关系有一定的了解,那么请大家针对上个环节的问题提出有效的猜想,并以小组为单位进行猜想的合理验证.
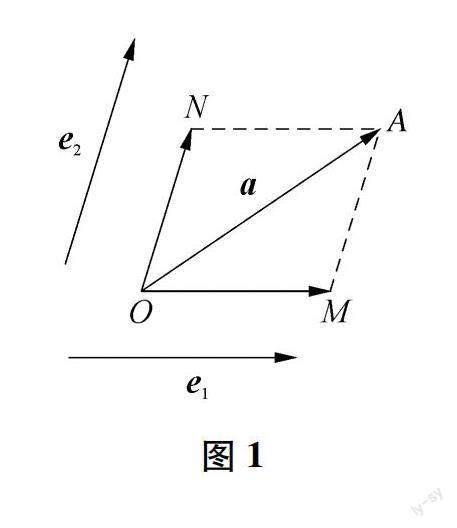
【猜想1】如果e1和e2位于同一平面但不共线,平面内任一向量a是可以用向量e1和e2来表示的.
教师:那对于平面内任一向量a,若用λ1e1+μ1e2來表示,那λ1、μ1是唯一确定的吗?
【猜想2】对于平面内任一向量a,若用λ1e1+μ1e2来表示,那λ1、μ1是唯一确定的.
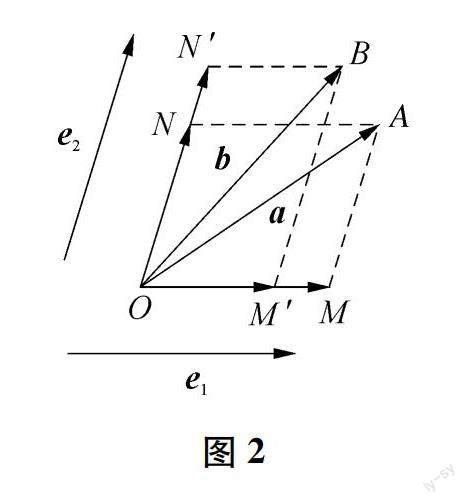
如图2所示,做平面内另一向量b,按照上一个猜想的作图方法得出λ2e1+μ2e2,根据几何直观给出的信息,可知λ2≠λ1,μ2≠μ1,则对于平面内任一向量a,若用λ1e1+μ1e2来表示,那λ1、μ1是唯一确定的.
教师:通过上述的猜想和证明过程,大家一定获得了平面向量的基本定理的大致内容,即在同一平面内的任一向量都是可以表示为其它两个不共线的向量的线性组合.
【设计意图】通过猜想、验证的形式让学生尝试以自己的思维方式去解惑,获得更加深刻、更加直观的知识理解,让学生在猜想中经历知识形成,明确学习方法.
环节三:加以应用,掌握定理
【设计意图】通过例题的设计训练学生的课堂学习成果,让学生尝试将新知识应用到实际问题当中去,获得自身数学能力的提升.
5 总 结
综上所述,尝试教学理论在实际数学教学课堂中的执行,能够有效促进学生尝试精神以及探究精神的发展,让学生不仅掌握相关的数学知识,还能获得智力、素质的双重提升,从根本上解决传统课堂中学生不思考、不交流的弊端,以学生的自主学习为动力,推动高中数学课堂教学的高效发展,同时也能有效促进教师自身的思想、道德和素质的提升.
参考文献:
[1] 孟改珍.基于尝试教学理论的高中数学教学设计[J].环球人文地理,2015(20):193.
[2] 陈文明.尝试教学理论在高中数学教学的应用[J].数学大世界,2017(1):39.
[3] 崔阳阳.浅谈“尝试教学理论”在高中数学教学中的应用[J].中学课程辅导(教学研究),2019(15):27.
[4] 陈平.“尝试教学法”在高中数学教学中的应用[J].中国校外教育:中旬,2016(2):139.
[5] 陈娜娜.尝试教学法在高中数学教学中的应用[J].中学生数理化(教与学),2018(12):17.

