一类具有时滞的SIR传染病模型的稳定性与Hopf分支

李伟南,廖茂新,李冰冰

(南华大学 数理学院,湖南 衡阳 421001)

0 引 言

近年来,国际上传染病动力学的研究极为迅速,大量的数学模型被用于分析各种各样的传染病问题。Kermack-McKendrick模型是传染病模型中最经典、最基本的模型,后来学者对该模型进行了不同角度的研究,在研究过程中,研究者们发现人体受到感染后,感染初期并不会表现出任何的症状,在一段时间之后,某些症状才会逐步表现出来[1-3]。研究初期人们并未考虑到时滞延迟因素,后来研究者们发现引入时滞(单或双时滞)因素,如疾病的潜伏周期,免疫周期以及恢复周期等得到的结果更加逼近实际[4-7]。对此方面的研究已经取得了很多成果,为更加有效的预防和治疗传染病提供了依据[8-9]。

基于前人既有的研究成果,本文在文献[10]一类具有非线性发生率和恢复率的修正SIR模型中,引入时滞得到以下模型:

(1)

式中:S(t)、I(t)、R(t)分别表示在t时刻易感染人群、已感染人群和恢复人群的数量;N(t)为t时刻的人口总数;K表示干预水平;α0和α1分别表示由于卫生保健资源的不足和亚人口感染造成的最小和最大人均恢复率;b为医院床位数量对传染病传播的影响;A为人口的出生率;β为接触率;μ为人口自然死亡率;γ为人群因病死亡率;τ为疾病的潜伏期。

考虑到生物学意义,假设该系统中所有参数均为非负数。

因系统(1)的前两个方程中没有出现R(t),所以只需考虑前两个方程即可,其中R(t)=N(t)-S(t)-I(t)。

(2)

1 模型的动力学分析

1.1 平衡点的稳定性

定理1当R0<1,无病平衡点E0是局部渐进稳定的;R0>1,无病平衡点E0是不稳定的。

(3)

系统(3)对应的特征方程为

(4)

特征值λ1=-μ,λ2满足

(5)

当R0<1时,假设λ=α+βi,则代入式(5)可得

由于R0<1,则Re(λ)<0,特征方程(4)所有根具有负实部,所以当R0<1时,无病平衡点E0是局部渐进稳定的。

则f(λ)=0必存在一个正实根,因此当R0>1,无病平衡点E0是不稳定的。

引理1当R0>1,τ=0时,系统(2)满足文献[10]中定理3的条件,则正平衡点(S*,I*)是局部渐进稳定的。

证明:系统(2)在正平衡点(S*,I*)附近对应线性近似系统为

(6)

则系统(6)可以改写为:

(7)

系统(7)的特征方程为:

λ2-(m0+m3)λ+m0m3+e-λτ((m2-m1)λ+

m1m3-m0m2)=0。

(8)

当τ=0时,方程(8)为

λ2+(m2-m1-m0-m3)λ+m0m3+m1m3-

m0m2=0。

根据文献[10]定理3有

(H1)m2-m1-m0-m3>0,

m0m3+m1m3-m0m2>0。

根据Routh-Hurwitz准则,当R0>1,τ=0时,正平衡点(S*,I*)是局部渐进稳定的。

引理2当τ>0时,方程(8)有一对纯虚根。

证明:当τ>0时,设λ=ωi(ω>0)是方程(8)的纯虚根。代入方程(8)进行分离实部和虚部可得

(9)

将式(9)两边平方之后相加可得

(10)

令Z2=ω,则式(10)变为

(11)

假设满足

则方程(11)存在唯一正实根

其中

显然,方程(10)仅有一个正实根

把ω0代入(9)式可得

(12)

将方程(8)对τ求导可得

计算再有

则有

根据上述引理2、引理3、引理4,结合Hopf分支定理,可以得到如下结论:

定理2当τ>0且R0>1时,若条件(H2)、(H3)满足,则当τ∈[0,τ0),τ0=min(τk)时,系统(2)的平衡点是局部渐进稳定的;当τ>τ0时,系统(2)的平衡点是不稳定的;在τ=τ0时,系统(2)在平衡点处出现Hopf分支。

2 数值模拟

当系数取A=1,β=0.5,k=1,μ=0.1,r=0.2,α0=0.2,α1=0.3,b=0.05时,系统(2)为

此时,R0=8.3>1,τ0=8.0,系统(2)存在唯一的正平衡点,且正平衡点是局部渐进稳定的,选择τ=7<τ0(见图1);在同样的参数条件下,选择τ=9>τ0,此时正平衡点不再稳定(见图2)。

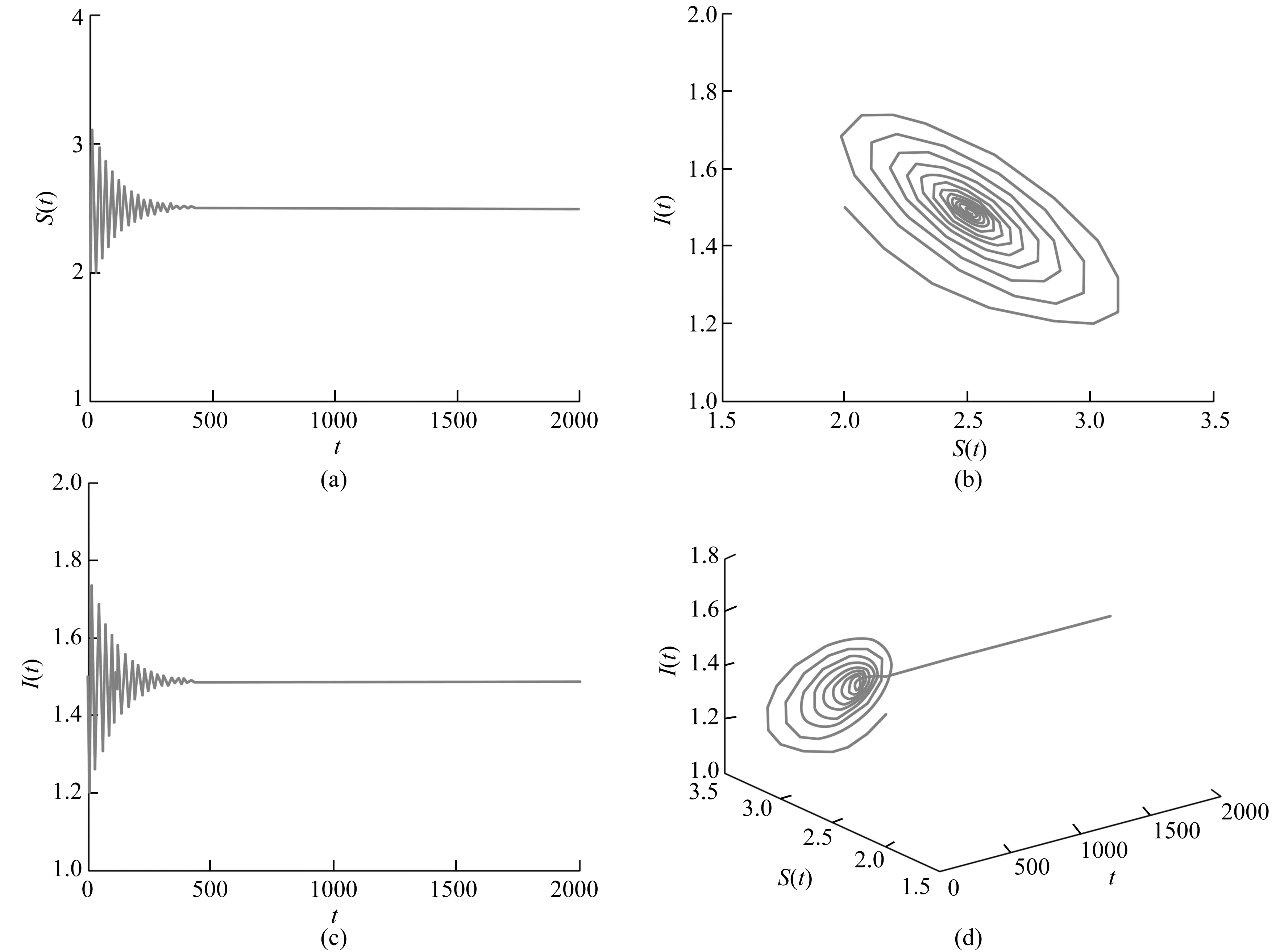
图1 系统(2)的平衡点渐进稳定(τ=7<τ0)

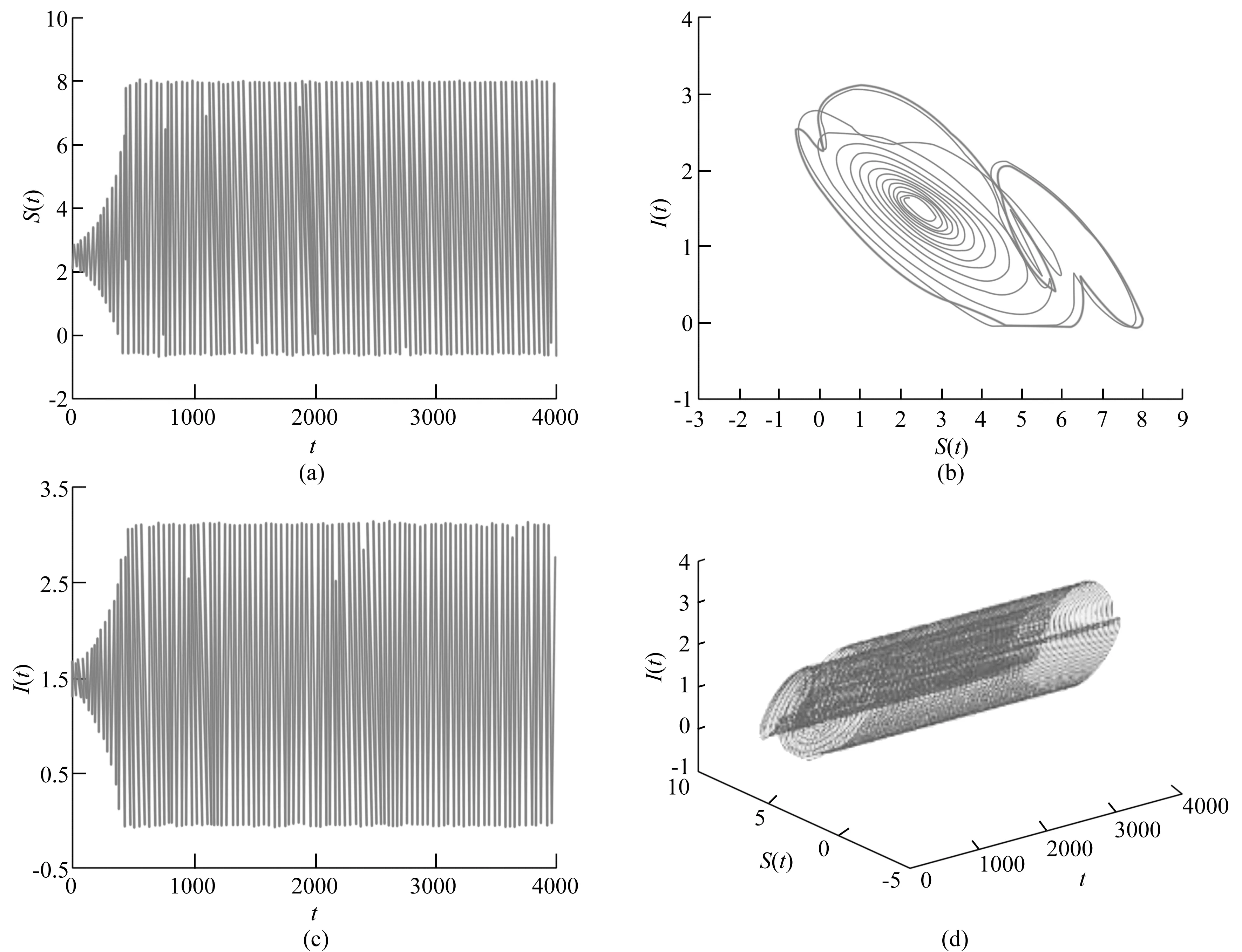
图2 系统(2)的平衡点失去稳定性,并产生Hopf分支(τ=9>τ0)

3 结 论

本文讨论了一类具有非线性发生率和恢复率的修正的SIR模型,在引入潜伏期作为时滞参数后,对地方病平衡点和正平衡点进行稳定性分析,得到了系统(2)局部渐进稳定和Hopf分支产生的充分条件,并利用数值模拟验证了理论分析的正确性。