一类具有非线性发病率的随机传染病模型的持久性
李 艳,储家蕊,廖新元
(南华大学 数理学院,湖南 衡阳421001)
0 引 言
众所周知,人类与传染病进行了漫长的斗争,在此期间也有不少数学家通过建立数学模型来对抽象的传染病进行研究和解读,其中按照传染病的模型类型可以划分为SIS,SI,SIR,SEIR,其中“S”,“E”,“I”,“R”的实际意义为:“S”,易感者 (Susceptible),指免疫力低下的健康人群,与感染者接触后容易患病;“E”,暴露者(Exposed),指接触过感染者但暂时无传染性的人群;“I”,感染者(Infectious),指已经感染传染病且具有一定传染性的人群,可以将传染病传播给S,将其变为I或E;“R”,康复者(Recovered),指病愈后具有一定免疫力的人群。而疾病的传播是由发病率来衡量的,常见的有标准发病率βSI/N或双线性发病率βSI[1-4]。但是,为了更好地模拟1973年巴里霍乱的传播,V.Capasso和G.Serio[5]提出了饱和非线性关联发病率Sf(I),从那时起,其他的非线性发病率如βIpSq,βSIp/(1+αIq)和βIPS/(1+αS)[6-7]相继被提出。研究发现,非线性发病率的传染病模型比双线性或标准发病率的传染病模型具有更为复杂的动力学,同时非线性发病率描述的传染病模型可能更适合现实,也能展现出更丰富的动态。本文基于以上研究的启发,通过分析流行病传播机理改进文献[8]的模型,得到以下具有非线性发病率的确定性SIS流行病模型:
(1)
在模型(1)中,S(t)和I(t)分别表示t时刻的易感个体和感染个体的数量。Λ表示出生和迁移在内的人口招募率,μ是自然死亡率,α是疾病死亡率,γ是疾病的恢复率,p是正整数,感染的传播受一个非线性发病率βSp(t)g(I(t))控制,其中β表示S和I间的传播系数,g(I)是I的一个连续可微函数,所有参数值均假设为非负的。
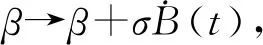
(2)
本文其余部分的主要目的是试图建立类似于确定性系统的随机系统的阈值动力学。
1 预备知识
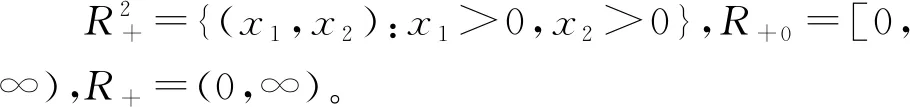
对于函数g(I),进一步引入以下假设
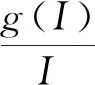
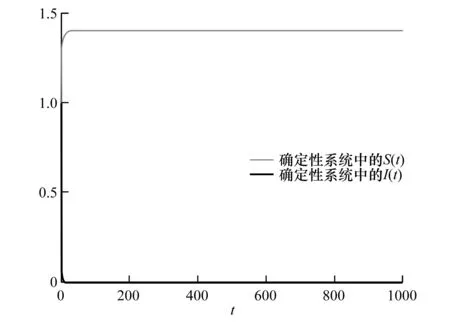
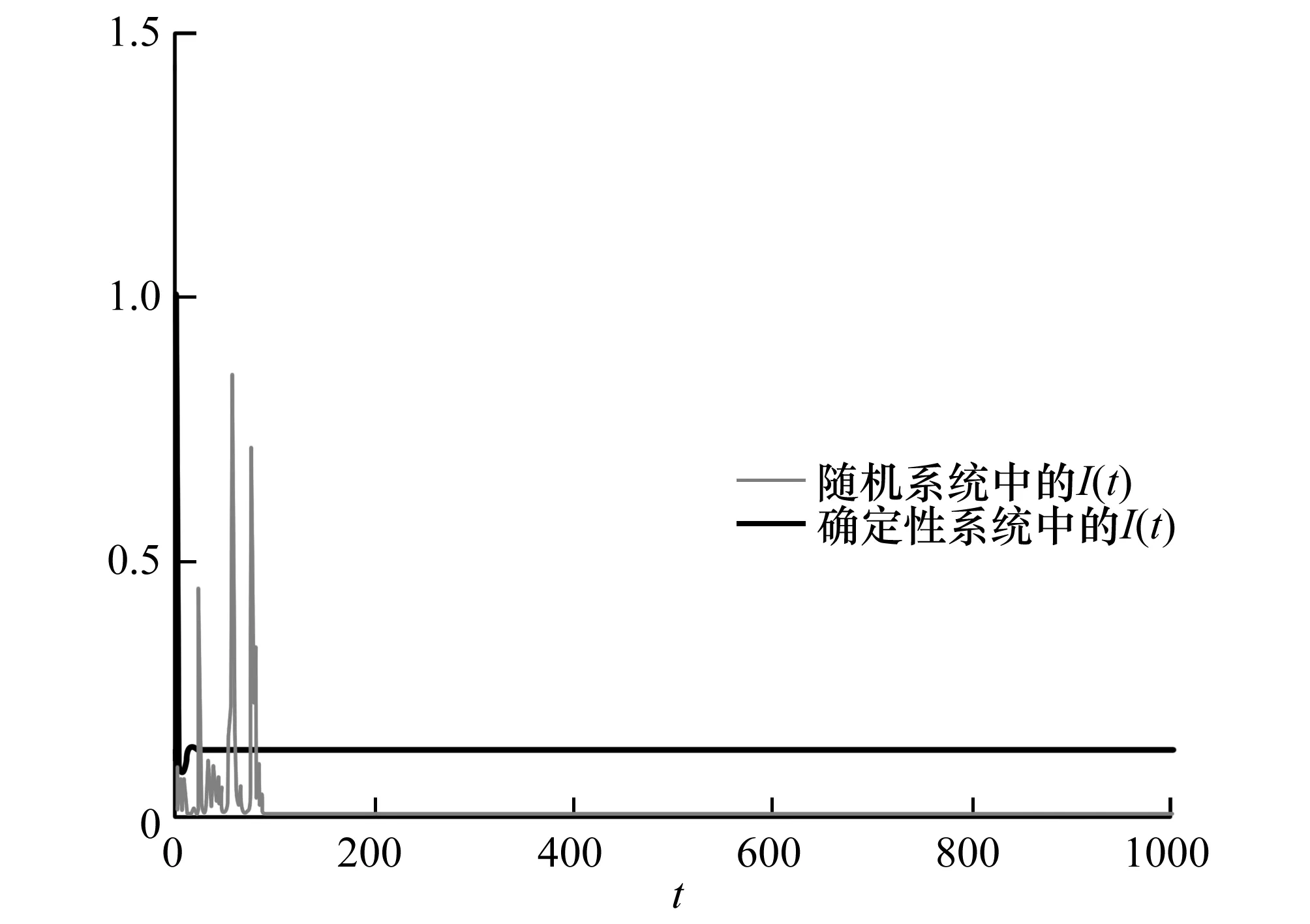
在假设(H)下,显然对于所有I>0,g(I)在R+0上是Lipschitz连续的,且0 dx=f(x,t)dt+g(x,t)dω(t)。 (3) 引理1[9-10]设x(t)满足式(3)和函数V(x,t)∈C2,1(Rn×R;R)。It公式可以写为 其中L是与式(3)相关的微分算子,且 设f是在[0,+∞)上的可积函数,记 为方便起见有以下定义。 定义1 对于系统(2) 2)如果存在一个正数λ,且满足 则疾病I(t)持久存在是几乎可以确定的。 利用文献[11]中的方法可以类似地证明以下两个引理。 注1 对于系统(2)满足以下不等式 d(S(t)+I(t))≤(Λ-μ(S(t)+I(t)))dt。 通过积分有 是一个不变集,那么从现在起,总是假设初值(S(0),I(0))∈Γ。 几乎成立。 容易看出系统(1)的平衡态满足 系统(1)有唯一的正平衡点E*,关于这些均衡的稳定性,参考文献[11-12],可以利用平衡稳定性原理类似地证明以下定理。 定理1 对于系统(1),有以下结论: 1)如果R<1,它有一个独特的稳定平衡点E0,这意味着疾病的灭绝; 2)如果R>1,它有一个稳定的正平衡点E*,这意味着疾病持久存在; 首先引入新的阈值 为了得到模型(2)中疾病在概率1上的灭绝性,首先建立以下定理。 定理2 对于系统(2) 对以上式子两边从0到t积分,并除以t,进一步得到 (4) 其次建立这样一个函数 具体证明如下: (5) 根据引理3可以得出 几乎成立。对(5)的两边取上极限 几乎成立。这意味着: (6) 对式(6)的两边取上极限有 几乎成立。当R*<1时,有 几乎成立。即 3)该证明与文献[13]类似,因此这里省略。 定理2证明完毕。 注2 定理2表明,当R*<1时,系统(2)的传染病几乎一定会灭绝,也就是说,大的随机白噪声扰动可以导致传染病灭绝。 定理3 如果R*>1,则疾病I是持久存在的,且I满足 证明 对系统(2)从0到t积分然后再除以t得到 然后可以得到 (7) 对式(7)从0到t积分再除以t (8) 通过使用Hölder不等式,有 (9) 情形一:当p是偶数,令p=2n,n∈N。 情形二:当p是奇数,令p=2n-1,n∈N。 有 (10) 其中 通过整理,式(10)可以写成 (11) 令Δ=max{Δi,i=1,2}。有 (12) 因此当R*>1时,疾病I是持久存在的,且满足式(12)。定理3证明完毕。 1)在模型(1)中,选择Λ=0.35,μ=0.25,p=2,β=0.55,γ=0.8,α=0.45,κ=2,q=3。通过计算得到:R=0.718 7<1,根据定理1,疾病在确定性系统中灭绝,数值模拟结果如图1所示;当Λ=0.48,其余参数不变,通过计算得到:R=1.351 7>1,此时疾病在确定性系统中持久存在,数值模拟结果如图2所示。 图1 S(t),I(t)在确定性系统中的变化趋势(R=0.718 7<1) 图2 S(t),I(t)在确定性系统中的变化趋势(R=1.351 7>1) 2)在模型(2)中,选择Λ=0.5,μ=0.25,p=2,β=0.55,γ=0.8,α=0.45,κ=2,q=3,σ=0.3。通过计算有:R=1.466 7>1,R*=0.986 7<1,根据定理2,疾病在随机系统(2)中几乎可以确定是灭绝的,数值模拟结果对比如图3、图4所示。 图3 S(t)在随机系统与确定性系统中的变化趋势(σ=0.3,R=1.466 7>1,R*=0.986 7<1) 图4 I(t)在随机系统与确定性系统中的变化趋势(σ=0.3,R=1.466 7>1,R*=0.986 7<1) 其次,在模型(2)中,当σ=0.1时,其余参数不变,通过计算有:R*=1.413 3>1,根据定理3,疾病在随机系统(2)中几乎可以确定是持久存在的,数值模拟结果对比如图5、图6所示。 图5 S(t)在随机系统与确定性系统中的变化趋势(σ=0.1,R=1.466 7>1,R*=1.413 3>1) 图6 I(t)在随机系统与确定性系统中的变化趋势(σ=0.1,R=1.466 7>1,R*=1.413 3>1) 以上数值模拟结果表明:在随机系统中,疾病走向灭绝或持久存在的条件依赖于白噪声干扰的强度,大的白噪声干扰有利于疾病的灭绝,相反,小的白噪声干扰将导致疾病的长期流行。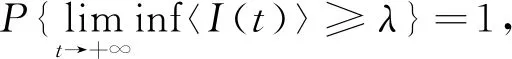


2 确定性系统的平衡稳定性分析

3 随机系统的灭绝性与持久性
3.1 灭绝性
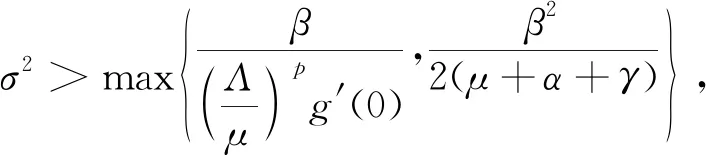
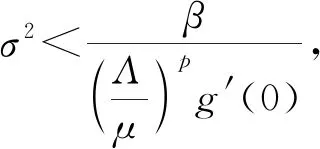


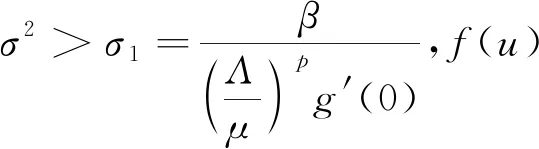
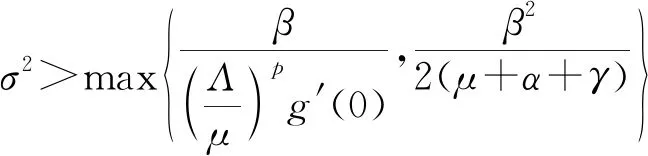
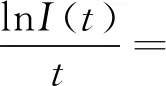

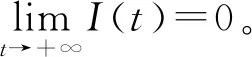
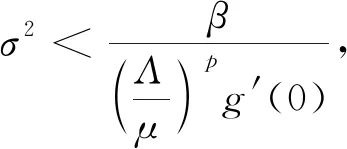
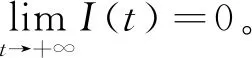
3.2 持久性
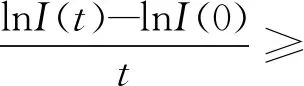
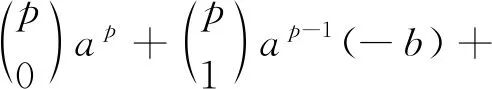

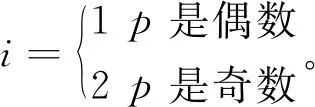
4 数值模拟





5 结 论

