数形结合思想在数列中的应用

王法金

【摘要】數与形是数学中两个基本的研究对象，它们有着内在的联系，而且可以互相转化，这一转化可被称为数形结合.数形结合的应用大致可分为两种情形：“以形助数”和“以数解形”.文章从“以形助数”和“以数解形”两个角度谈数形结合思想在数列中的应用，旨在让一线教师认识到数形结合思想的重要性并熟悉其应用.

【关键词】数形结合；数学思想；数列；图像；应用

引 言

数形结合是通过数与形的相互转化解决数学问题的一种重要思想.数形结合的实质是把抽象的数学语言与直观的图形语言结合起来，即将代数问题几何化、几何问题代数化.数形结合可解决的问题比较多，下面以数列为例，谈谈数形结合思想在数列中的应用.

一、以形助数

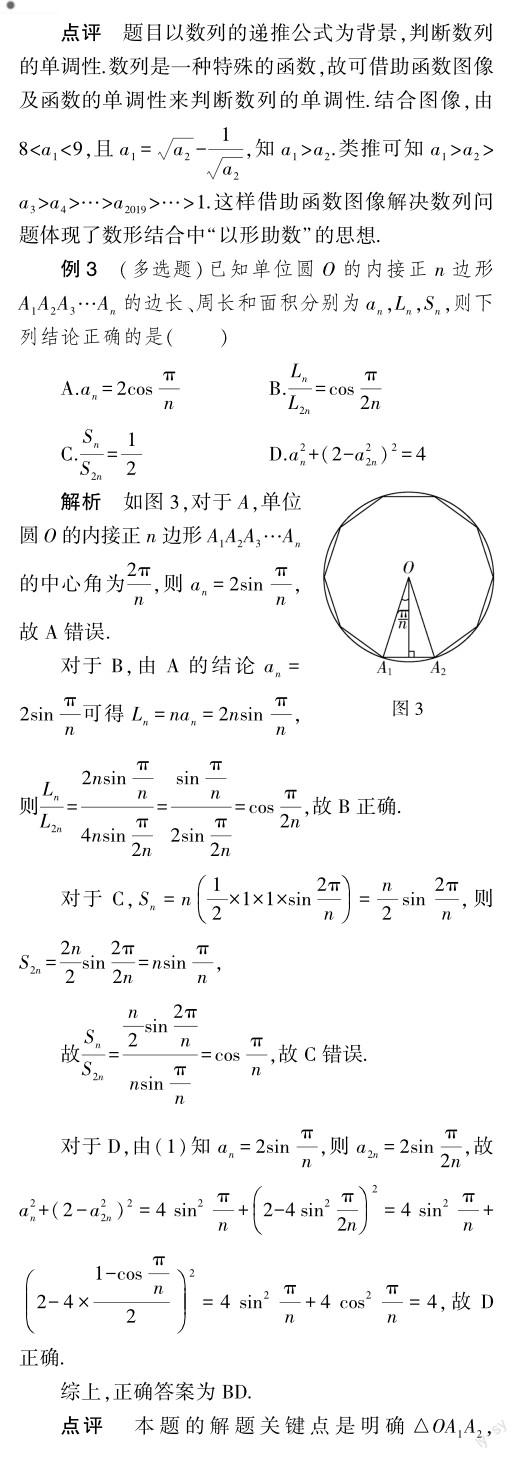
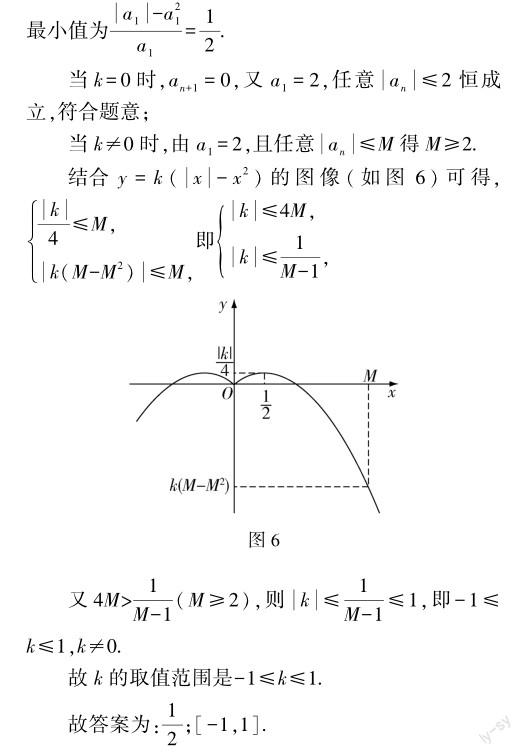
点评 解本题的过程中，解题者根据题意作出相关函数的图像，再结合图像的特点进行代数运算，使问题得解，这一过程体现了数形结合中“以数解形”的思想.

结 语

作为教师，不仅要教会学生解题方法，还要教会学生解题的思想.数形结合是一种重要的数学思想，其将“数”与“形”紧密联系在一起，应用数形结合思想解题时，既可以“以形助数”，又可以“以数解形”.教师应该在解题教学中渗透数学结合思想，帮助学生梳理题目的框架与解题的思路，从而提升学生的解题能力.

【参考文献】

[1]陈元斌.数形结合思想在高中数学教学中的应用与分析[J].数理天地（高中版），2023（23）：66-68.

[2]张东林.数形结合思想在中学数学的应用[J].中学数学，2012（8）：84-85.

[3]曹莹，李鸿昌.一道数列最值问题的解法探究[J].高中数学教与学，2019（19）：15-16.