逆向思维在小学数学解题中的应用技巧

张海军

【摘要】逆向思维是从问题的结果出发或从其他角度对问题进行转化的一种思维方式，如逆用数学公式、反证法、转化法，等等.逆向思维对于降低学生解题难度有着重要意义，研究其应用技巧可提高数学习题教学质量，提升学生解题能力.文章结合小学数学解题案例论述了逆向思维在解填空题、选择题、运算题、应用题时的应用技巧，旨在提高学生的逆向思维能力，推动小学数学解题教学发展.

【关键词】逆向思维；小学数学；解题教学；应用技巧

现阶段的小学数学命题方式越来越新颖.对于一些问题，学生利用正向思维很难快速解决.对此，提升学生的思维灵活性，使其掌握应用逆向思维解决问题的方法，可帮助其攻克解题难点.逆向思维的应用类型有很多，只有“对症下药”，才能保证解题的快速性与准确性.为此，小学数学教师有必要研究逆向思维在解决小学数学不同类型问题中的应用技巧，并将其巧妙融入数学解题教学，为不断丰富课程内涵，推进学生综合发展做好准备.

一、逆向思维在填空题中的应用技巧

填空题是小学数学试卷上的必有题型，通常将要求的结果以横线代替，要求学生根据题目给出的已知条件进行分析运算，并将正解写在横线上方.小学数学填空题的特征是题目信息少、跨度大、覆盖面广，往往以简练的题目考查学生对数学概念、定理、公式等基础知识及数学思想方法的掌握情况.学生在数学学习过程中，难免会遇到难以用常规思维解决的填空题.此情况下，教师应引导学生根据题目特征酌情选取反证法、逆用数学公式等逆向思维解题法，以此实现快速求解.比如，在人教版二年级上册“表内乘法（一）”一课的习题教学中，有填空题如下：

解析 按照正向思维，学生应基于小勇妈妈给出的金额进行除法列式、减法列式，得到还剩下2元的结果.但是这样的思维方式无法确定给出的金额到底是多少.这时，教师可引导学生应用逆向思维进行分析：小勇最后剩下2元钱，在买零食之前应剩下的钱应是2+4=6（元）.根据“小勇先用这些钱的一半买了玩具”，可以明确“6元”与小勇买玩具的金额相等，之后进行除法的逆运算：6×2=12（元），即可得到妈妈给的总钱数为12元.结合图1所示内容进行逆推，可进一步提高解题效率：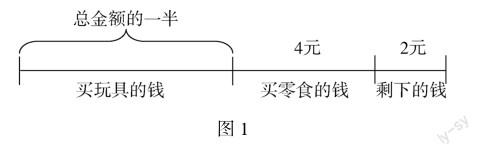

解决难以利用正向思维推理数值的填空题时，教师可引导学生运用逆向思维，同时借助图示、实物等多种工具将题目给出的抽象信息具象化，之后结合问题中的等量关系采取倒推法进行逆向运算，达到轻松求解的目的.

二、逆向思维在选择题中的应用技巧

小学数学选择题由题干与备选项两部分构成.题干常以陈述句或疑问句的形式出现，通过呈现问题情境激发学生的解题兴趣；备选项以数字、短语等形式出现，通常为与题干有着直接关系的备选答案.小学数学选择题大多为单选题，备选项中只有一个正确答案，其他为干扰项.遇到难以通过正向思考解决的选择题时，学生可运用逆向思维进行推理，或直接将题目给出的选项代入原题选定正确答案.比如，在人教版二年级下册“表内除法（一）”一课的习题教学中，有选择题如下：

例2 甲、乙两名学生在玩猜数游戏.甲说：我心里想着一个数，给这个数加上9，再取和的一半应是5.乙猜想这个数是（ ）.

A.1 B.2 C.3 D.4

解析 这一问题直接给出结果，要求学生逆推条件.按照常规思路分析问题显然具有一定的难度，为此，教师可引導学生运用逆向思维，以结果为起点，逆向推理：甲心想的数加上9后和的一半是5，说明和为5×2=10，向前逆推，可明确这个数为10-9=1.也可换一个角度思考：这一问题给出了四个选项.先根据题目给出的数量关系列出算式，将甲心想的数用“□”代替，得到（□+9）÷2=5.将1，2，3，4四个数值分别代入原式，代入后等式仍然成立的数即为正确答案.

解决问题结果（或最后结论）是已知数据（或起始条件）这种类型的问题时，教师需要引导学生综合考虑题目中的已知、未知数量关系，确定正向、逆向运算顺序，再将所要求的数量用数学符号代替，列出正向算式，之后根据逆推的思路进行正向算式、逆向算式的互化，从而得到所求数的具体数值，之后将所得数值与题目给出的具体选项进行对照，即可轻松选出正确选项.除此之外，教师还可以引导学生将选择题给出的备选答案反向代入原题当中，若代入后原题给出的数量关系仍然成立，说明代入数值正确，若不成立则说明代入数值并不是正确答案.

三、逆向思维在计算题中的应用技巧

计算题是以算理、算法为核心考点的问题，包括加、减、乘、除及混合运算等类型.常规的计算题可直接套用计算公式进行求解，但一些简便运算问题、数字填空问题需要运用逆向思维将其转化.

（一）解简便运算题

简便运算题以加（乘）法交换律、结合律，乘法分配律，除法的性质为主要考点，要求学生将复杂算式化简求值，且该过程应尽量避免使用笔算的方法.一些运算题并不以a+b=b+a，a×（b+c）=a×b+a×c等常规形式出现，学生需要运用逆向思维对算式中的量进行转化.比如，在人教版四年级下册“运算定律”一课的习题教学中，下列简便运算问题便需要学生应用逆向思维求解.

例3 化简求值.

（1）36×111+888×8；（2）999×78.

解析 针对第（1）题，按照正向思维应对原式采取竖式计算方法，不符合简便运算要求.通过逆向思考，发现其中的888可被拆解为8×111，那么原式就可被转化为36×111+8×111×8，根据乘法结合律、交换律、分配律，可得原式=36×111+111×64=（36+64）×111=11100.针对第（2）题，学生可换一个方向出发，思考999可用哪些算式表示，之后基于转化的思想逆构简便运算模型：999×78=（1000-1）×78，之后按照乘法分配律进行简便运算即可得到问题答案为77922.

解简便运算问题时，教师可引导学生先应用正向思维分析算式，若算式较为典型，可直接代入运算律进行求解；若算式形式新颖，可应用逆向思维对算式中的“数”进行转化，通过逆向推理将原式转化为符合运算定律计算模型的算式，之后求解.

（二）解竖式谜题

竖式谜题是基于纵向排列数字计算的谜题，用于训练学生的运算思维，通常包括一个乘法计算和一些额外的限制条件.这类问题一般要用逆向思维来解决.以人教版四年级上册“三位数乘两位数”一课的习题教学为例，学生可用逆向思维解决如下竖式谜题.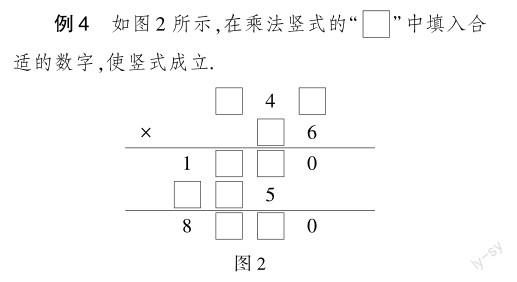

解析 可分三步解答此谜题.第一步，根据两个乘数的末位数字相乘得0，可以逆向推得第一个乘数的末位可能是0或5，再根据第一个乘数的末位数字与第二个乘数十位数相乘的末位数字是5，可以确定第一个乘数的末位数字就是5.第二步，根据第一个乘数与第二个乘数个位上的6相乘得一千多，逆向推得第一个乘数的百位数字可能是2或3，分别计算245×6=1470，345×6=2070，由此断定第一个乘数为245.第三步，因为竖式中的积为八千多，所以能确定第一个乘数与第二个乘数十位上數字的积是六百多或七百多，由此确定第二个乘数的十位数字是3.综合三步推理，可解答谜题：245×36=8820.

解答乘法竖式谜题时，学生需要将积的关键特征作为解题切入点，运用逆向思维分析两个乘数各位数字之间的关系，之后进行逆向推理，补充谜题中的空白部分.

四、逆向思维在应用题中的应用技巧

应用题是小学数学题的重要构成部分，用以检验学生迁移应用数学概念、原理、公式解决实际问题的能力，主要包括行船问题、归一问题等类别.一些应用题难度较高，难以直接列式解答.这种情况下，教师需要引导学生应用逆向思维.

（一）行船问题

行船问题是由现实生活中的航行问题加工得来的.一般情况下，此类问题以船速、水速为主要信息，求两点之间距离.对于一些较为简单的问题，可直接利用“（顺水速度+逆水速度）÷2=船速”等数量关系式代入求值.针对一些形式新颖、内容复杂的问题，需要运用逆向思维.比如，在人教版五年级上册“简易方程”一课的习题教学中，学生可用逆向思维解决如下行船问题.

例5 一艘货轮往返于甲、乙两地之间，由甲地到乙地是顺水航行，由乙地到甲地是逆水航行.已知货轮在静水中的速度是每小时20千米，由甲地到乙地用了6个小时，由乙地到甲地所用的时间是由甲地到乙地所用时间的1.5倍，水流速度是多少？

解析 水流速度、行船速度、静水速度息息相关.但是，此问题并未直接给出货轮的行船速度，也未给出甲、乙两地之间的路程，很难代入公式直接求解.为此，教师可以运用逆向推理的思维方法提出问题，让学生围绕问题梳理解题思路，如：（1）要求水流速度，根据题意需要什么条件？（2）要求行船速度，根据题意需要什么条件？（3）题目中有哪些数量关系可以被利用？根据系列问题，学生可以明确：题目给出了静水速度，用行船速度加或减静水速度可得水流速度；行船速度可以根据“路程÷时间=速度”这一公式求得；从甲地到乙地、从乙地到甲地所行驶的路程是相同的.之后，假设水流速度为每小时x千米，则由甲地到乙地的货轮行驶路程为[（20+x）×6]千米，由乙地到甲地的货轮行驶路程为[（20-x）×6×1.5]千米，可得方程（20+x）×6=（20-x）×6×1.5，解方程可得水流速度为4千米/时.

应用逆向思维解决行船问题时，应将题目的问题作为切入点，从问题出发思考解决问题需要的确切条件，之后将其中的一个（或两个）未知条件作为要解决的问题，再找出解这一个（或两个）问题所需的条件.通过逐步逆推的方式找到解决问题的已知条件，完成解题.

（二）归一问题

归一问题属于复合应用题，要求学生解题时按照已知条件先求出单位量，再利用单位量列式计算，求出问题结果.解决此类问题时，学生需要灵活运用逆向思维找出单位“1”是什么，之后结合题目要求列式求解.比如，在人教版六年级上册“分数除法”一课的习题教学中，学生可用逆向思维解决如下归一问题.

应用逆向思维解决归一问题的思路有很多.最重要的是把握问题给出的数量关系，如倍数关系、和差关系等.先通过逆向推理等方式求出单一量或倍比关系，再结合求出的已知信息展开计算，求出所要求的数量.

结 语

逆向思维的应用化解了正向思考受阻的困境，具有化复杂为简单、化抽象为直观等功能.小学生在数学学习中不可避免地会遇到无法利用常规思考方式解决的数学难题，这时教师可指导学生灵活运用逆向思维，采取逆用定义、逆用数学公式与运算法则等手段反过来思考问题，通过变式、间接证明等方法解决数学难题.

【参考文献】

[1]黄文锦.逆向思维在小学数学解决问题教学中的研究应用[J].数学学习与研究，2022（36）：41-43.

[2]周国文.逆向思维在小学数学教学中的应用[J].读写算，2022（35）：64-66.

[3]廖昀.小学生逆向思维的培养策略[J].江西教育，2021（18）：68.