初中数学平面几何题型的解题技巧研究

吴霖杰

【摘要】勾股定理作為一个最基本的几何定理，为解答初中数学平面几何题型提供了思路，教师应在初中数学解题教学中，向学生传授勾股定理解题技巧，使学生学会巧妙解题，发散数学思维.文章简要介绍了勾股定理，紧接着分析了勾股定理在初中数学平面几何题型中的实际解题应用技巧，提出利用勾股定理解答周长问题、面积问题、最短路径问题、证明问题等.同时指出，教师应在夯基、精讲、常练基础上，指导学生利用勾股定理解答初中数学平面几何题型，培养学生的解题能力.

【关键词】初中数学；平面几何；解题技巧

勾股定理证明了平面直角三角形三边关系问题，即在任何一个平面直角三角形中，两条直角边的平方之和都一定等于斜边的平方.平面几何是初中数学的重点，也是难点.《义务教育数学课程标准（2022年版）》在数与代数、图形与几何、统计与概率、综合与实践四个领域组织课程内容，平面几何属于图形与几何领域.在该领域，学生应进一步建立几何直观，提升推理能力，解决抽象问题.分析平面几何问题，其解题思路为：将一般图形转化为特殊图形，然后根据特殊图形的特殊规律进行求解.而直角三角形，是转化平面几何图形的最有效图形之一，通过在原图中添加辅助线，构造直角三角形，将平面几何问题转化为直角三角形相关问题，然后利用勾股定理展开计算，不仅有助于学生高效解决问题，而且能够提高学生的数形结合能力，培养其发散思维.教师可以具体的初中数学平面几何题型为例，传授学生勾股定理解题技巧.

一、勾股定理在初中数学平面几何题型中的解题技巧

（一）利用勾股定理解答三角形周长问题

例1 已知在△ABC中，AB=13，AC=15，BC边上的高AD为12，求△ABC的周长.

题型与解题技巧分析 此题型为初中数学平面几何基础题型.想要确定一个三角形的周长，需要先确定其三边长.但在一些三角形周长问题中，无法通过题目已知条件直接判断其三边长，对此，解题者可构造直角三角形，利用勾股定理降低解题难度.本题给出三角形其中两条边的长度以及另一条边对应的高，解题者可以根据已知条件构造直角三角形，借助勾股定理计算原三角形第三条边的长度，即BC的长.但是根据题目已知条件，无法确定高AD在△ABC中的具体位置，应画图并进行分类讨论.当高AD在△ABC内部时，先通过勾股定理分别计算出CD与BD的长，再通过求和得到BC的长.当高AD在△ABC外部时，需要延长CB，故而在求出CD与BD的长后，需要通过求差得到BC的长.利用勾股定理解答三角形周长问题，关键便在于画图与分类讨论，充分考虑未知边长的每一种可能.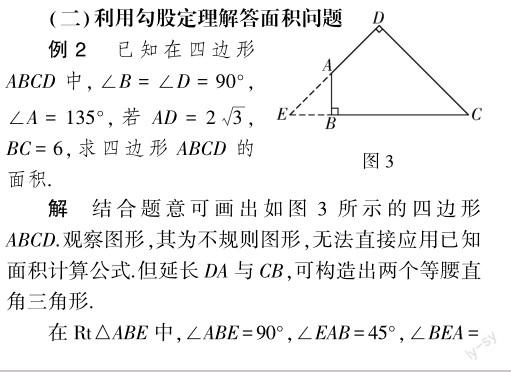

题型与解题技巧分析 初中数学中，一些不规则图形面积问题无法结合已知公式展开计算，而是需要构造直角三角形，将不规则图形转换为两个或两个以上直角三角形，代入勾股定理，具体步骤为：（1）观察图形，分析其特点.（2）引入辅助线，构造直角三角形，确定相关线段长度.（3）借助直角三角形面积间接计算不规则图形面积.本题中，待求图形为不规则四边形，解题者可以延长线段CB，DA，使其延长线交于点E，构造两个直角三角形，确定相关线段长度.之后，通过计算△CDE与△ABE的面积差，即可成功求出四边形ABCD的面积.利用勾股定理解答面积问题，关键在于引入辅助线，割补不规则图形，构造直角三角形.

（三）利用勾股定理解答最短路径问题

例3 如图4所示，在一个无盖圆柱形玻璃杯内壁B点有一滴蜂蜜，蜂蜜距玻璃杯底部5cm.玻璃杯整体高度为14cm，底面周长为32cm.若不计玻璃杯厚度，一只蚂蚁在玻璃杯外壁A处出发去吃蜂蜜，最短应爬行多远的距离？（蚂蚁与玻璃杯口的竖直距离为3cm）.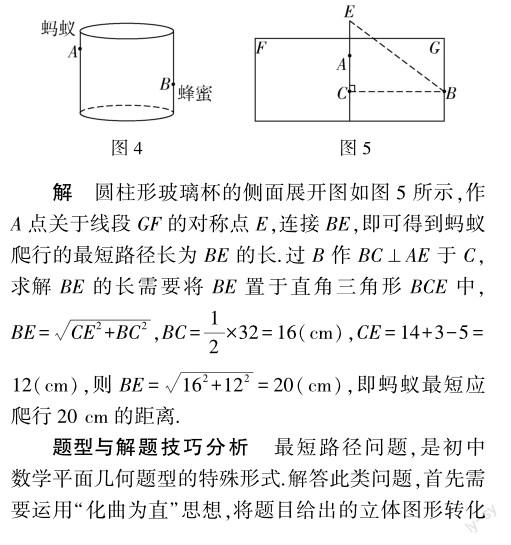

题型与解题技巧分析 证明问题是初中数学平面几何题型的重要组成部分，包括证明图形线段长度关系、角度大小关系、直线位置关系等题型.即便题目所给条件较为复杂，解题者也可以从复杂信息中挖掘简单提示，如勾股定理.分析可通过勾股定理进行解答的初中数学平面几何证明问题，其分类如下：（1）题目所给条件未直接体现勾股定理，但证明对象与勾股定理相关.（2）题目所给条件与勾股定理联系紧密.对于前者，解题者应在证明过程中构造直角三角形，将已知条件逐渐转化至同一直角三角形中；对于后者，解题者应寻找或构造直角三角形，直接由勾股定理展开推理，得到边长关系.利用勾股定理解答证明问题时，解题者需要先结合所给条件判断题目特征，再根据题目特征灵活解题.

（五）利用勾股定理解答折叠问题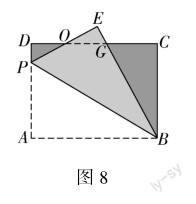

例5 如图7所示，长方形ABCD的长和宽分别为8和6.已知P是宽AD上的一点，现沿着BP折叠△ABP，使PE与CD相交于点O，BE与CD相交于点G.如果OD=OE，线段AP的长是多少？

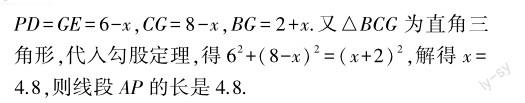
题型与解题技巧分析 折叠问题也是常见的初中数学平面几何题型之一，可分为根据折痕求角的度数、线段的长、重合部分的图形面积等题型.解答折叠问题，不仅需要运用轴对称、四边形等知识，而且需要引入勾股定理，具体思路为：（1）根据折痕运用轴对称的性质，确定对应点，分析对应线段位置与大小关系.（2）根据折叠前后的特殊点和线段，构造直角三角形.（3）立足直角三角形，利用勾股定理、三角函数计算待求问题.本题为“求线段的长”折叠问题，满足勾股定理解题特点.在长方形ABCD中，折叠前后的對应角与对应边相等.故而想求出线段AP的长度，不妨设未知数x，即AP=x.在此基础上，图中所有线段均可用未知数表示.用相关未知数结合勾股定理列出方程，求出x，便可得到线段AP的长.当然，在题目给出相对简单的条件时，也可以直接运用勾股定理，“跳过”列方程步骤.

二、初中数学平面几何题型解题技巧的指导要点———以“勾股定理”为例

一线教师以勾股定理为切入点研究初中数学平面几何题型的解题技巧，是为了认识初中数学平面几何题型的更多解答方法，更是为了提升教学水平，指导学生从多角度分析和解决初中数学平面几何问题，培养学生的问题解决能力.故而在以上研究基础上，教师应进一步分析初中数学平面几何题型解题技巧的指导要点，下面笔者以勾股定理为例进行阐述.

（一）夯基

利用勾股定理解答初中数学平面几何题型，要求学生具备扎实的勾股定理知识基础.教师应在此层面上，重视初中数学勾股定理教学，实现“夯基”目标.教师可以在实际教学期间，整合游戏化教学、情境教学、问题教学、任务型教学、层次化教学、翻转课堂等教学方法，循序渐进地指导学生探究勾股定理，从而使学生充分经历勾股定理的猜想、推理、认识、理解、实践、掌握过程，形成发散的勾股定理解题思维.比如，在讲解勾股定理时，教师可以借助“赵爽弦图”与“毕达哥拉斯树”创设情境，为学生搭建“数形并茂”的学习平台，指导学生先观察情境中的数学图形，再挖掘和讨论其所蕴含的数学思想.其间，教师应巧妙点拨学生“找规律”，促使学生发现直角三角形三边的“平方”规律，奠定扎实的勾股定理认知基础.再如，在根据教材例题指导学生运用勾股定理时，教师可鼓励学生扮演“小老师”，讲解不同题目的分析思路和解题步骤，深化学生思维，强化“夯基”效果.

（二）精讲

掌握勾股定理在不同初中数学平面几何题型中的解题技巧，要求学生准确区分初中数学平面几何题型与勾股定理的内在联系，建立结构化的思维系统.教师应在此层面上，对涉及勾股定理的初中数学平面几何题型进行精讲，全面启发学生思维.教师应完善初中数学平面几何习题训练，每呈现一个特殊题型，都必须为学生精讲解答过程.对此，教师可以结合课堂互动预案，精心设计动态课件.课上，教师先通过课件呈现题目，鼓励学生自由讨论、分享思路.紧接着，教师借助鼠标控制动态课件，依次出示解答步骤.出示题目解答步骤前后，教师都应给予学生充足的讨论时间，然后对学生讨论结果进行补充讲解，使学生准确把握解题技巧.全面讲解例题后，教师还可以设计对比归纳课件，将初中数学平面几何不同题型及其勾股定理解题技巧进行汇总，帮助学生加以区分.

（三）常练

纸上谈兵不如实际演练，面对初中数学平面几何题型，学生想要快速判断其特点、选择正确的勾股定理解题技巧，必须达到熟能生巧的状态.因此，教师应组织学生常练.教师应将“常练”与“题海战术”进行区分，为学生精选典型题目，避免为学生施加过大综合实践压力.对此，教师可以将中考数学真题视为习题资源库，关注历年中考真题，提炼其中的平面几何典型题目，创新设计勾股定理与平面几何测试题，进而对学生定期进行习题训练.在此基础上，教师还可以督促学生整理错题，建立错题集，以便随时查缺补漏，实现巩固练习.

结 语

总之，为提高学生解答初中数学平面几何题型的效率，教师有必要向学生传授勾股定理解题技巧.具体来讲，教师应明确勾股定理的本质及解题价值，总结初中数学中常见的平面几何题型及其勾股定理解题技巧，抓住“夯基”“精讲”“常练”三大要点对学生进行指导，促使学生创新解决问题，提高解题能力.

【参考文献】

[1]林劲松.浅析勾股定理的应用探究[J].读写算，2022（36）：132-134.

[2]赵霞.例析勾股定理常见的应用类型[J].中学数学，2022（20）：82-83.

[3]万广磊.探究神奇的勾股定理[J].初中生世界，2022（42）：44-45.