AutoCAD的工程计算方法应用研究
孔晓林


摘 要 AutoCAD系统是一款平面绘图软件,其强大的应用功能也是工程设计的辅助工具,该软件具备的基本数学计算功能以及平面几何关系分析功能,可以将工程设计过程中的某些复杂计算问题转化为平面几何图形,利用AutoCAD的功能去解决问题,快速获得精确答案。
关键词 AutoCAD系统;工程计算;平面几何
中图分类号:G712 文献标识码:B
文章编号:1671-489X(2016)20-0019-03
AutoCAD系统作为广为流行的平面绘图软件,除了基本的平面绘图、立体建模功能外,还为图形管理提供了强大的应用功能,如图形的组织、图形检查、图形比较等,进行多种图形格式的转换、各种数据交换。其开放式的结构还允许用户以此作为平台开发应用程序,受到广大用户的欢迎和喜爱。AutoCAD系统除了基本的这些功能之外,还具备用于基本的数学计算以及平面几何关系分析功能,为工程设计过程中的计算需求提供了方便,体现在以下几个方面。
1 基础的数学计算功能
在各种设计中会用到大量的数字基础运算,用计算器计算很方便,但计算过程不能保存,验算、检查只能从头开始,非常不便。AutoCAD系统内嵌的lisp应用程序具备各种计算功能,如a1+a2+a3+a4…等多个数值相加,可以在命令行输入(+a1 a2 a3 a4…)的lisp运算指令,可以像一条命令单独运行,系统直接给出答案。此计算方法同样适合各种形式的混合基础运算,如加减乘除混合运算,(/a1(-c1 c2)),数学表达式为a1/(c1-c2),而且这样的计算可以在系统中穿插运行,不影响系统中的图形文件操作,过程自动保存在文本界面中,便于随时查看,也可以单独保存为文档文件输出,非常便于设计过程的数据检验与备查。
2 三角函数计算功能
工程设计中会遇到许多三角函数相关的计算,这些计算需要专业的技术资料支持,而利用AutoCAD的绘图功能可以将这些专业性计算转化为平面图形问题。如直角三角形的尺寸标注可能只有两个直角边长(或其他两个参数),但系统却记录着有关该直角三角形的所有信息,如斜边长度、两个锐角大小、面积等信息,可以利用系统某种手段直接、间接地得出。
如求sin26°=?,如果没有函数表,计算过程是很困难的。在AutoCAD系统中可以将三角函数计算转化为平面图形问题,绘制一锐角等于26°的直角三角图形,绘图时将斜边取为整数值,如1或10,则26°锐角对应的直角边长度值大小即是sin26°的量值或10倍量值,精度值可以达到小数点后8位,足可以满足绝大部分设计要求。
对于已知函数值求角度的问题,则是问题的逆向考虑,根据函数项目,利用绘图功能还原符合要求相似的三角形,角度自然可以查出。如已知cosα值,求角度大小。可以设定斜边长度为1,那么邻边长度则为cosα的值,将这个直角三角形绘制出来,相对的夹角自然得出。
在工程设计中,许多与角度有关的工程计算其实都是三角函数与边长间的关系应用的具体体现。
1)斜度的计算。工程中经常用斜度表示两个倾斜的表面间的位置关系,其本质是两个表面夹角余切的大小。如果需要知道夹角的大小或相关邻边大小,只需按1:1比例画出平面图形,利用系统查询功能测量夹角大小即可,而相关联的其他尺寸也可以测量出来。
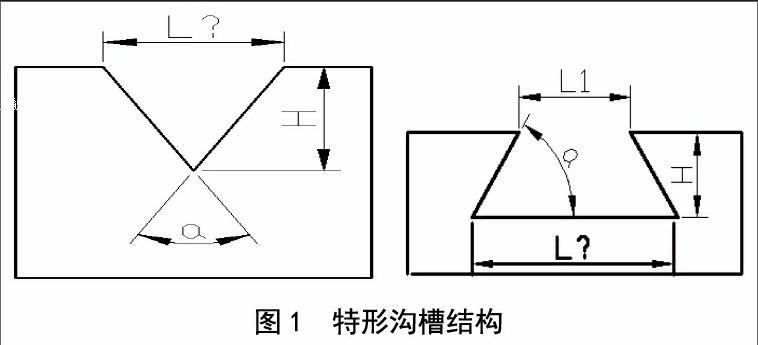
2)在加工生产中,许多的尺寸计算都用到了三角函数的计算,如图1所示的结构是工程中常见的特形沟槽结构,通过给定的尺寸画出完整图形,未标注的宽度尺寸可以方便地量出。
加工生产中计算毛坯的直径大小,本质上也利用了函数关系,如已知多边形零件边长尺寸,如果其毛坯选择圆棒料,通过绘图很容易获得其外接圆,再考虑加上余量,棒料的直径就确定下来了,节省了计算时间。
3)零件表面间位置关系判断,也是将三角函数计算转化成平面图形的几何关系。如图2所示的零件,中心孔底面结构为球面(R>φ),制定加工此孔工艺方法时,必须先判断在钻孔达到孔深后,刀尖能否破坏球面表面,这就需要根据这个曲面的几何尺寸计算出球面深度,然后计算出刀尖的长度进行比较。计算过程虽然没有什么难度,但需要一定的计算量,如果用绘图系统则可以简单地解决这个问题:按尺寸1:1比例绘出结构图,二者关系一目了然,还可以直接得出加工球面时的刀具轴向走刀深度。
总之,在AutoCAD中绘出相关结构图形,利用标注、查寻功能,可以方便得出有关角度、边值,从而满足各个方面的计算要求。
3 工程设计中的求值应用
AutoCAD系统的计算功能不局限于纯粹的数学计算,它的计算功能可以扩展到解决工程问题,解决设计中的体积、面积、周长等方面的需求。
1)传动设计中的皮带长度、包角计算。图3的皮带传动中,确定了两个皮带轮的直径、中心距后,需要确定皮带长度以及两个带轮的包角大小。在AutoCAD系统中1:1绘出皮带传动图,修剪获得皮带的轮廓,通过查询功能可以获得皮带的长度;如果有皮带的宽度、比重,可以获得重量;大小带轮的包角可以通过查寻功能或测量获得。
2)对于一些外围的规则或不规则的图形或一定区域,如图4所示的一个公园区域,想获得其外围的周长(或面积),计算起来一定很麻烦。把这个图形放在AutoCAD系统中,由系统提供的查询功能可以很方便解决这个难题。通过完整描绘出这个区域的轮廓线,把轮廓线编辑成多段线,直接查询多段线长度和所围区域面积大小即可,还可以将多个类似区域的面积进行加减运算。
3)在分析物体的受力和分析受力平衡问题方面,AutoCAD系统的图形编辑功能更是强大。力有大小、方向、作用点三要素,在进行受力的矢量和计算时,解析法过于麻烦,而普通的图解法的精度和准确度取决于技术人员的技术水平和认真程度,用AutoCAD系统进行图解物体受力、矢量和计算,其精确度甚至超过解析法。在AutoCAD系统中可以利用图形准确表达力的大小、方向、作用点三要素,通过实体编辑图形,正确复制(或移动)每个单独的力,使它们首尾相连,完成矢量和计算,获得0误差的量值大小、准确矢量方向,简单方便,精确度无可挑剔。
4 机构的构件间位置关系
工程设计中经常要解决组成机构的构件间位置关系、一些运动部件的关键位置,如在连杆机构设计中,极限位置的确定以及求压力角求解问题,计算起来很麻烦,也可以在AutoCAD绘图系统中用图解法解决。
如图5为已知尺寸的四杆机构,设连架杆12为曲柄原动件,14为机架,如何确定摇杆34的极限位置呢?摇杆摆角大小怎么计算?最小压力角呢?由平面连杆机构基本特性可知,这几个主要参数都与摇杆的极限位置有关。根据运动规律和几何关系判断,连架杆34两个极限位置分别处于杆连架12、23拉开共线、重叠共线时两个位置上,在AutoCAD绘图系统中运用绘图技巧,很容易找出3点的两个极限位置。
如图6所示的绘图过程:先绘出水平直线14;以4点为圆心、L34为半径绘制一个圆1;以1点为圆心、(L23-L12)为半径绘制一个圆3;以1点为圆心、(L23+L12)为半径绘制一个圆2;圆1分别和圆2、圆3有一个有效的交点,即为两个极限点。在AutoCAD绘图系统中利用此方法,可以准确地求得3点的两极限位置,同时获得3点两极限位置坐标点,将两个图形绘在一起,可以快捷、正确地测出摇杆摆角、压力角等参数大小。
总之,作为广泛应用于工程设计中的绘图软件,还是一个工程设计辅助工具,AutoCAD的功能是很强大的。除了最基础的绘图、图形处理功能外,AutoCAD还有许多应用方面的功能没有被挖掘。如果在工程设计中把复杂的计算转换为图形表达,通过系统的辅助功能有效地把复杂问题转化为简单问题,可以提高工作效率,保证计算的正确度,减小工作强度。
参考文献
[1]程绪琦.AutoCAD2006教程[M].北京:电子工业出版社,2008:6.
[2]江方记.AutoCAD高级应用[M].重庆:重庆大学出版社,2010:4.
[3]张诚坚,何南忠.工程数学:计算方法[M].北京:高等教育出版社,2008:1.
[4]毛友新.机械设计基础[M].武汉:华中科技大学出版社,2012:6.

