极值点偏移问题的类型与破解策略

李金莲 丁国盛

【关键词】导数；极值点偏移问题；构造法；对称函数；解题策略

根据极值点左、右两边的增长速度不同，极值点偏移问题分为极值点左偏和极值点右偏两种情况.破解极值点偏移问题的关键是构造对称函数.解题者需要根据不同的类型，构造出不同的对称函数，然后结合函数的单调性进行证明.

一、极值点偏移的特征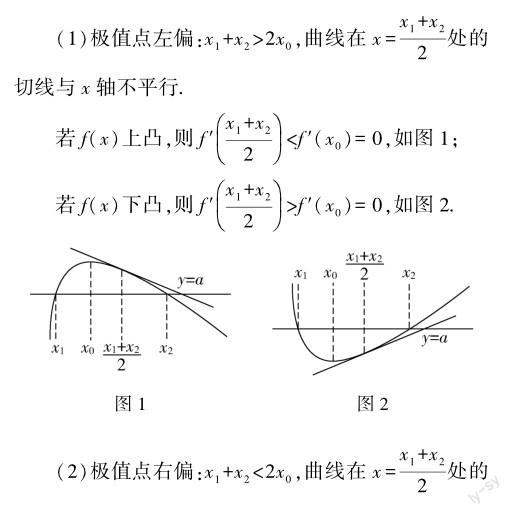

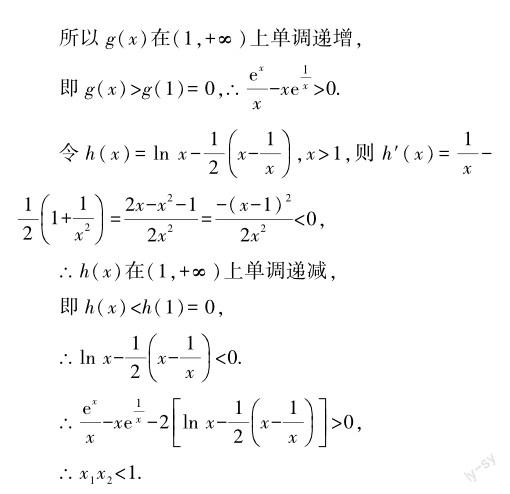
點评 本题是极值点偏移问题，故考虑构造对称函数，则问题等价于证明F（x）>0，不过直接证明F（x）>0是比较困难的，这里采用“各个击破”的办法来处理，使得问题得以解决.

结 语

极值点偏移问题对于学生来说是个难点，教师在教学中要把极值点偏移问题的类型与破解方法给学生讲解透彻，既要讲清楚“需要构造什么函数，构造函数之后如何根据单调性进行证明”，又要将极值点偏移问题进行分类，适当地给学生做强化训练.学生只有真正地理解了极值点偏移问题的类型及破解策略，而且通过题型训练，做到熟能生巧，在考试中遇到时才能从容应对.

【参考文献】

[1]罗文军.极值点偏移问题破解策略[J].中学生数理化（高二数学），2018（3）：3-5.

[2]曾雪萍.通过函数构造解决极值点偏移问题[J].数学学习与研究，2020（16）：128-129.

[3]张君，李武学，胡泽余.构造法在极值点偏移问题中的应用———从2022年高考全国甲卷21题谈起[J].中学数学研究，2022（12）：43-45.

[4]李鸿昌，徐章韬.关于对数平均的一个不等式的推广[J].数学通报，2023，62（8）：50-52.

[5]李鸿昌.一道新高考导数压轴题的解法探究[J].高中数学教与学，2021（15）：22-23.