“脚手架”：让数学思维真正“长”出来

杨雪梅

［摘  要］ “脚手架”的巧妙搭建可以让学生的数学思维真正“长”出来，也可以提高课堂教学效率。文章结合“智慧广角”一课的教学，谈一谈如何采取具有针对性的教学策略，在彰显教学智慧的同时，为学生搭建指向数学思维的“脚手架”，同时促进学生数学素养的形成与发展。

［关键词］ 脚手架；数学思维；条理性；灵活性；深刻性

数学教学是思维活动的教学，思维在教学中不可缺席，有益的思考方式与思维习惯是教师教学中首先需要考虑的因素。因此，教师应将培养学生的思维置于教学的首位，探索出适切而有效的教学方式，提升学生的思维能力。培养的着手点该置于何处呢？笔者认为，“脚手架”的巧妙搭建可以让学生的数学思维真正“长”出来，也可以提高课堂教学效率。下面，结合“智慧广角”一课的教学，笔者谈一谈如何采取具有针对性的教学策略，在彰显教学智慧的同时，为学生搭建指向数学思维的“脚手架”，同时促进学生数学素养的形成与发展。

一、用心设计“问题链”，搭建思维起点处的“脚手架”，让思维更具条理性

教材是知识的精华，也是教学的资源，倘若教师对教材的领悟程度不足，则会影响教材目标的实现程度。对于本课，教材中提供的学习素材是小学生在日常生活中常见的小汽车和摩托车，由于有了亲切感，学生就有了解决问题的生活经验，从而能更加积极主动地投入探索之中。探索时，教材采用的是列举法。学生对列举法不陌生，但他们是否能通过列举法完成探究呢？这是教师需要考虑的问题。

为了清楚了解学生的思维起点，笔者设计了如下问题：鸡与兔共8只，共有腿26条，则鸡几只？兔几只？学生借助自身的学习经验解决问题。纵观解答情况，可以发现大部分学生运用了“凑结果”的方法，虽然解答过程中也有策略性调整，但由于缺乏一定的条理性，故他们无法清晰展现思维过程。有了对学生思维起点的准确把握，下一步自然是想方设法将列举法引向全体学生。如何设计才能让学生有条理地思考呢？在深思熟虑之后，笔者通过设计简单的“问题链”来唤醒学生思维。

师：一辆摩托车有几个轮子？一辆小汽车呢？停车场停有摩托车和小汽车共3辆，一共可能有多少个轮子？说说你的思考过程。（学生展开火热的思考）

生1：有2辆摩托车和1辆小汽车，一共8个轮子。

生2：有1辆摩托车和2辆小汽车，一共10个轮子。

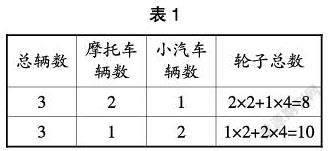
师：嗯，有没有办法让你们的想法更加清晰呢？如果我们将想法填入表1中，大家的思路就一目了然了。

师：咦，为什么总辆数不变，轮子的总数会不同呢？

生3：因为摩托车和小汽车的轮子个数不一样。

师：非常好，看来你们已经对此类题目中的数量关系有了初步感悟，下面就让我们一起进入今天的学习。

认识：以上环节中教师关注到学生的思维，用心设计适切的“问题链”，引领学生逐步走上探索之路，引发学生对新知的好奇。在学生的脑子里呈现各种轮子总数之后，教师巧妙设置“表格列举法”，通过这样的演示，让学生头脑中的一一列举的认识变得清晰起来，从而自主体悟和感受其中的数量关系，感悟数学的条理性。

二、悉心组织探究活动，搭建思维烦琐处的“脚手架”，让思维更具灵活性

每个儿童都期待自己可以作为研究者的身份进行数学探究，而灵活性思维是数学探究得以成功的前提，也是创新思维的必备条件，这就需要教师创造机会、开放课堂，给予学生更多的主动权。但课堂一旦开放，对教师的教学决策就提出了更高的要求。教师需要深入钻研教材、悉心组织教学，切实抓住学生的思维特征，搭建思维烦琐处的“脚手架”，引领学生进行数学思考，在交往互动中促进学生去发现、研究和探索，让学生的思维更具灵活性。

在本课的自主探究环节，笔者开放了课堂，抛出问题“24辆摩托车和小汽车共有多少轮子”，引发学生的深度思考。学生在已有经验的引导下，有的想到通过一加一减来假设两种车型的辆数，并经过反复调整探寻出正确答案；有的从1辆小汽车、23辆摩托车开始通过一加一减来假设两种车型的辆数，但由于列举过程中发现结果与答案差之千里，故也会跳跃地列举，以求快速探得正确答案；还有一些学生选择从各12辆开始列举，并在首轮列举后分析数据，以求快速获取答案。无论如何，以上三种方法均是通过假设、比较、计算、调整等方式实现的，与小学生的认知规律和已有经验相吻合。

在学生自主探究之后，笔者设计了对比展示的环节，以此为学生搭建思维烦琐处的“脚手架”，让学生在分析、对比和反思中切实体会不同列举法的优劣性。当逐一式列举、跳跃式列举及居中式列举这三种列举方式同时呈现在学生眼前时，大部分学生体会如下：在数据较大的情况下，先分析后列举是首选，也可以边列举边分析，总之居中式列举与跳跃式列举都是不错的选择，而逐一式列举这种不变通的方式既烦琐又耗时，需要摒弃。

认识：以上环节中，正是有了学生磕磕碰碰的探究经历，才有了分析、对比和反思之后的深刻感受，才能为之后的学习和生活提供帮助，也正是因为各种思考方式的碰撞，才能真正意义上提高学生思维的灵活性。在探究中，除了悉心的设计，还需要给学生留白，让学生不断改进、不断调整，最终走向成熟。

三、精心策划难点突破口，搭建思维困顿处的“脚手架”，讓思维更具深刻性

学习的过程就是发现、提出、分析和解决问题的过程，在这样的经历中，学生收获的不仅仅是知识本身，更重要的是通过问题的解决获得思维的自然生长。在教学中教师需要精心策划，搭建思维困顿处的“脚手架”，为学生突破重难点提供帮助，让学生的思维更具深刻性。

一般来说，解决鸡兔同笼的问题采用的是假设法，那么之前的猜想和列举则是理解假设法的前提。而将列举法中的规律迁移应用于假设法中，让学生领悟假设法的算理是学生学习的难点。如何打破这一思维难点？笔者以为，画图法能有效破解这一思维困境，基于此，设计了如下教学过程。

师：大家一起来看这里的情境图，那么假设24辆均为小汽车，共有轮子多少个？请大家列式计算。（教师用课件呈现图示）

生1：4×24=96（个）。

师：与结论中的86个相差多少？

生2：96-86=10（个），多了10个。

师：为什么多10个呢？

生3：这其中有部分摩托车，并非小汽车。

师：那我们就还原这部分摩托车，如何？一共还原了多少辆摩托车？如何列式？

生4：10÷2=5（辆）。

师：该算式中，10表示的是什么？2又表示了什么？5呢？

生5：“10”表示的是假设24辆全为小汽车后，比实际多出的10个轮子。“2”表示的是4-2=2（个），即1辆小汽车比1辆摩托车多2个轮子；“5”则表示的是需要还原的摩托车有5辆，如果将算式变为10÷（4-2）=5（辆），就更容易理解了。

师：非常好。现在请大家再假设24辆均为摩托车，如何探索？请小组合作，并说一说其中的道理。

……

认识：这里，正是有了情境图这一直观形象的前提，才为学生后续理解假设法的算理铺平了道路，让他们之后的探究和生成变得顺理成章。通过情境图这个“脚手架”，有利于学生集中更多的注意力去科学探究，从而完美实现教学目标。

总之，数学教学的本质是帮助学生建构数学知识，促进学生思维的生长。教师用心设计、悉心组织、精心策划，适切搭建思维起点处、烦琐处、困顿处的“脚手架”，充分组织学生去探索、讨论、交流和互动，让学生自然形成对数学的认识，让他们的思维更具条理性、灵活性和深刻性。当然，教学中无论采用哪种类型的“脚手架”，教师都需要从学生的思维发展过程出发，在适当的时候搭建适切的“脚手架”，由此才能让学生的数学思维自然“长”出来，同时促进学生数学素养的形成与发展。