基于心理育人的初高等数学教学衔接思考
王燊 张露 林妹珠

【摘要】笔者在大学生心理健康教育中发现,高等数学学习困难引发的学业焦虑是大学新生面临的主要问题之一.对此,文章从心理育人的角度出发,对高等数学教师和大一新生进行访谈,并对高中数学教材、高等数学教材、高中数学课程标准等材料进行文本分析,探索了初高等数学教学衔接上的相关问题及成因,并提出初高等数学教学衔接的三角模型:学习内容、师生沟通和心理适应,其分别为构成良好衔接的三个维度:认知维度、关系维度和情感个性维度.
【关键词】心理育人;高等数学;教学衔接
【基金项目】福建省教育科学规划立项课题“‘课程思政在高等数学课程中的应用探索”(编号FJJKCG19-157);福建农林大学横向课题“创新创业类课程《学习管理和心理健康发展》的实践研究”(编号KH200090A).
高等数学是高等学校大部分专业必修的一门基础课程.“内容多、课时緊、不均衡”已成为高数教学普遍存在的问题,而在教学过程中,来自学生“我很差”“我不会”“我很笨”的声音也影响了一些授课教师的教学信心,甚至部分大一新生在高等数学的学习上体验到“困难”“挫败”和“失落”,并由此引发了严重的心理问题,如焦虑、抑郁,进而放弃努力.心理健康教育课程在“学习心理”专题环节进行了调查,发现大多数学生的主要学习困扰来自高等数学.
心理育人质量提升体系被列为“十大育人”体系之一,在《高校思想政治工作质量提升工程实施纲要》中,其与课程、科研、实践、文化、网络、管理、服务、资助、组织等方面协调合作,体现了以生为本、因材施教的教育理念.在心理育人的工作体系中,育人主体包含且不限于心理健康教师、思政教师、全体师生及员工.培养担当民族复兴大任的时代新人是心理育人的最终目的,培养身心健康、智力良好、人格完善、关系协调的大学生是大学育人的基本目标.
中学与大学的教学衔接对大学生入学阶段的学业适应有着重要作用,对学生的心理健康成长有着特殊意义.良好的教学衔接可以提高学生的适应能力,增强其学习效能感,增进其自信心并提升心理健康水平.
本研究以促进新生适应高等数学学习和提升心理健康水平为目标,通过师生访谈、文本分析等方法,对初、高等数学教学衔接中存在的问题及原因、心理影响和可能的解决方法提出了思考和建议.
一、教学实践中发现的问题
初等数学和高等数学的衔接是高等数学教学的一个重难点.一线教师在长期的教学实践中也发现,学生的数学能力参差不齐,学习内容有时空差异.通过师生访谈和教材文本分析,笔者发现初高等数学教学衔接主要存在下列问题.
(一)内容存在重合和断层
通过教材比对发现,无论是小学、中学还是大学,都很注重培养学生的数学能力,不过在内容的选定上,不同阶段、不同地区有较明显的差异.“函数”是现代数学中最基本的概念,它不仅是贯穿高中数学课程的主线,更是高等数学的主要研究对象.高等数学主要围绕幂函数、指数函数、对数函数、三角函数、反三角函数等五类基本初等函数展开微积分学的讨论,而中学阶段涉及的初等数学的主要教学目标在于理解这些函数的概念、性质、应用等基础知识,可以说,初等数学为高等数学奠定了重要的学习基础.
然而,教师在教学实践中发现:(1)一些重要的知识出现明显的断层.以“三角函数”为例,《普通高中数学课程标准(2017年版2020年修订)》(以下简称高中课标)仅对正弦、余弦、正切三类三角函数(包括它的概念、性质、几何解释、基本关系、恒等变换等)做出了明确的学习要求,而对于实际问题中同样常用的余切、正割、余割三类三角函数及反正弦、反余弦、反正切、反余切等四类反三角函数并未正式提及.(2)一些内容出现重复,如“一元函数导数及其应用”这一部分教学内容,在高中课标中,其对于导数的应用从两个阶段提出学习要求:一是在选择性必修课程中提出“能利用导数求某些函数的极大值、极小值以及给定闭区间上不超过三次的多项式函数的最大值、最小值,体会导数与单调性、极值、最大(小)值的关系”;二是在选修课程的A类及B类课程中,对“导数与微分”部分均提到“会利用导数讨论函数的极值问题”.而这一知识点在《高等数学D》第三章第二节“函数性态分析”中也有详细介绍.
(二)动机和认知因情绪产生趋避冲突
学生的学习不仅受到认知的影响,同时受到情绪的影响.在高中阶段,无论是自主学习能力较强的学生还是自律能力较弱的学生,都可以在长期的考试应激、教师辅助规划、家长督促推动下完成反复、持续的学习,然而到了大学阶段,测验频次锐减,重复学习次数极低,来自老师和父母的外部推动力极速下降,这些突如其来的变化导致许多学生一时间找不到学习的方向和适合的学习方法.大学一年级是激活学生终身学习内在动力的重要阶段,内在的情绪和情感体验对激发学生的内生动力尤其重要.高等数学的学习特点容易让学生产生失望、挫败等情绪体验,从而产生回避行为,但因为常年的学习惯性和部分学生的考研驱动力,高等数学的重要性在学生心中依旧名列前茅,所以,学生的高等数学学习会出现认知和情感的不协调,“既想学又怕学”的趋避冲突异常突出.
二、问题的原因分析
在师生访谈的过程中,大部分教师认为做好教材内容衔接并不困难,只要了解中学教学要求,就可以采取有效措施做好补充,而学生其实在学习动力、学习方法、情感态度上受到的阻力更大.从学习动力和情感态度来看,很多学生表现出明显的畏难情绪,这是影响其学习动力的一个重要因素.教师无法很好地了解学情,学生对于学习目标感到迷茫,师生之间的沟通缺乏动力,这些都使一些学生处于大部分时间“躺平”、小部分时间“挣扎”的状态.也有部分学生由于高考数学失利,导致在认知层面知道自己要好好学习数学,但是情感上不愿意面对.从学习方法和学习行为来看,大学更注重概念理解、原理推导及知识的应用和迁移,也就是我们常说的“举一反三”,这与中学时靠反复练习强化理解的方式大相径庭,也在一定程度上导致不少学生“一听就会,一做就废”.
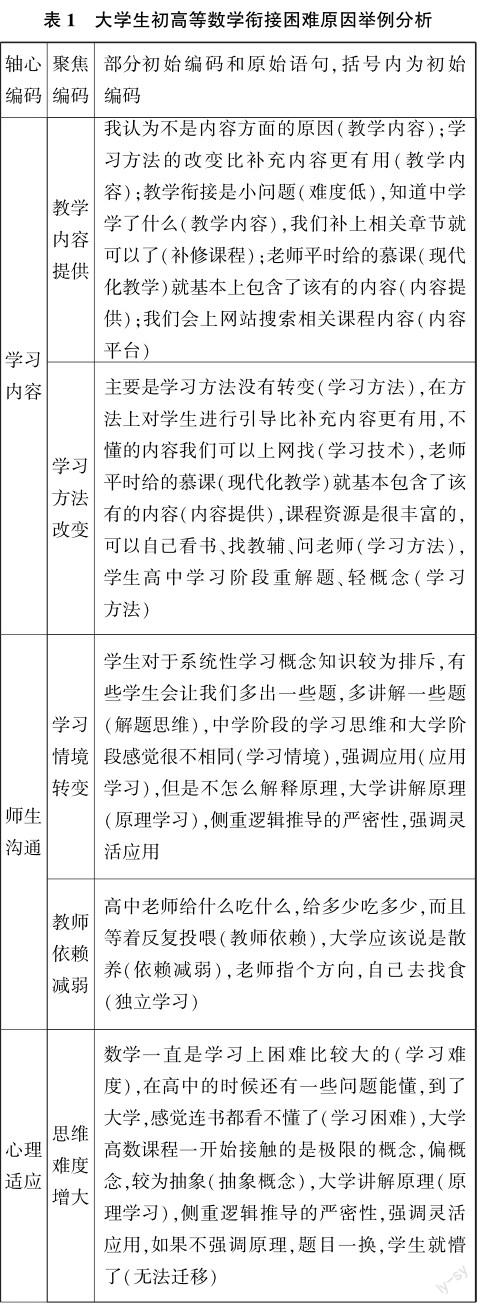
使用扎根理论对师生访谈资料进行编码,可得出大学生初高等数学衔接困难的原因,举例如下,其中节选部分初始编码、聚焦编码,并形成轴心编码.

三、教学衔接的三角模型:学习内容、师生沟通和心理适应
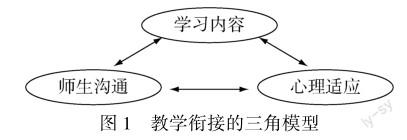
基于心理育人目标的初高等数学教学衔接,学习内容作为衔接的载体,体现了教学衔接的认知维度;师生沟通是教学衔接的关系维度,提供了认知、情感和个性发展的社会支持;心理适应是学习内容衔接的情感保障和发展基础,体现了教学衔接的情感和个性维度.学习内容、师生沟通、心理适应三者相互影响,构成良好的教学衔接所必备的稳定的三角模型(如图1).
(一)学习内容视角
从学习内容来看,大学不同专业对高等数学课程的教学要求不尽相同,在教学内容的衔接上,很难提出统一的模板,但是有一些可供推广的方法.一是构建“学习材料包”,根据不同专业对应的不同难度高等数学教材(含高数A、高数B、高数C、高数D)先行准备预习课程视频、相关练习和练习答疑视频、自测问卷、自测试卷、网络学习资源清单等.以概率和统计为例,有些学生要求把排列组合和古典概型再講一遍,故在教学内容的衔接上,教师需要详细了解高中数学的内容,然后把一些前期需要的内容放在平台上.二是实行“助教先行辅学”.一般学校中的助教是高年级学生或者相关专业研究生,助教辅学的内容并非仅限于数学知识本身,还可以分享自身学习高等数学的经验和教训,以及对高等数学的感受和思考,从而引发大学新生对高等数学的好奇心和亲近感.三是强调自主学习.一线教师可以编辑所授学科的自主学习手册,在开课前发给班级学生,部分有较强学习动力的学生可以根据自主学习手册进行学习.学习材料包和自主学习手册根据每学年不同的要求可以适当调整修订,而由助教形成的老带新团队也可以形成良好的互动.
(二)师生沟通与心理适应视角
关于师生沟通和心理适应方面,教师可以更多地考虑如何用好“课堂”和“网络”这两个重要的沟通平台.首先,相对于高中教师而言,大学教师由于授课量大、学生数多,关注每一名学生的特点的可能性较低,因此,提升沟通质量是加强师生沟通的关键.课堂是学生和老师接触时间最多的地方,提升课堂师生互动质量是高数教学的重中之重.提升课堂沟通质量的心理基础是信任,即学生相信老师的能力,也相信老师对自己的关心和信心,老师相信学生的潜力,相信每一名学生都能够学好高等数学.善用“吸引力法则”建立良好的信任关系是沟通的第一步.其次,为了更好地了解学生的学习背景和当前学习困难,高数教师和心理健康教师可开展合作教学,通过问卷、自我成长报告等方式快速获得学生的学习背景资料,并通过Nvivo等质性分析软件筛查需要重点关注的学生,最大限度地做到精准帮扶.最后,师生可共同思考、构建问题解决的方案,由高数教师、学生和心理健康教师分工合作,以高等数学学习为契机,促进学生的自我发展.
结 语
从高中到大学是学生人生发展过程中的重大跨越.面对不同的学生,心理育人的任务意义重大,方法亦应与时俱进.高等数学是很多新生入学后学习中遇到的第一个考验,顺利地通过这一考验可对他们的心理成长和发展赋予积极的效能感,增强他们克服困难的信心.数学之美在于将混乱的变为规则的,将无序的变为有序的,将繁复的变为简洁的,在初高等数学教学衔接过程中,让学生体验数学之美,同样将混乱、无序、繁复的心理状态调整为规则、有序、简单的心境,也体现了高等数学心理育人的意义.
【参考文献】
[1]马建青,杨肖.心理育人的内涵、功能与实施.[J].思想理论教育,2018(9):87-90.
[2]任子朝,赵轩.论高考数学的育人功能[J].数学通报,2020,59(11):14-20,52.
[3]朱立明.高中生数学学科核心素养测评指标体系的构建[J].教育科学,2020,36(4):29-37.
[4]凯西·卡麦兹.建构扎根理论:质性研究实践指南[M].边国英,译.重庆:重庆大学出版社,2009.

