2022年高考全国甲卷圆锥曲线试题探究与变式

四川省成都市石室中学 (610015) 李贤江 成都市电子科技大学实验学校 (611731) 黄 信

圆锥曲线一些解答题常常含有极点与极线的背景.极点与极线是高等几何的重要理论，是解决圆锥曲线一些复杂问题的巧妙方法.学生如果了解极点与极线理论，那么就可预知结果并且减少大量繁琐运算.

极点与极线的定义：如图1，圆锥曲线外一点S，过点S作圆锥曲线的两条割线SA和SC，分别交圆锥曲线于A、B，C、D四点，直线AD和BC交于点E，直线AC和BD交于点T，直线ST是点E关于该圆锥曲线的极线.

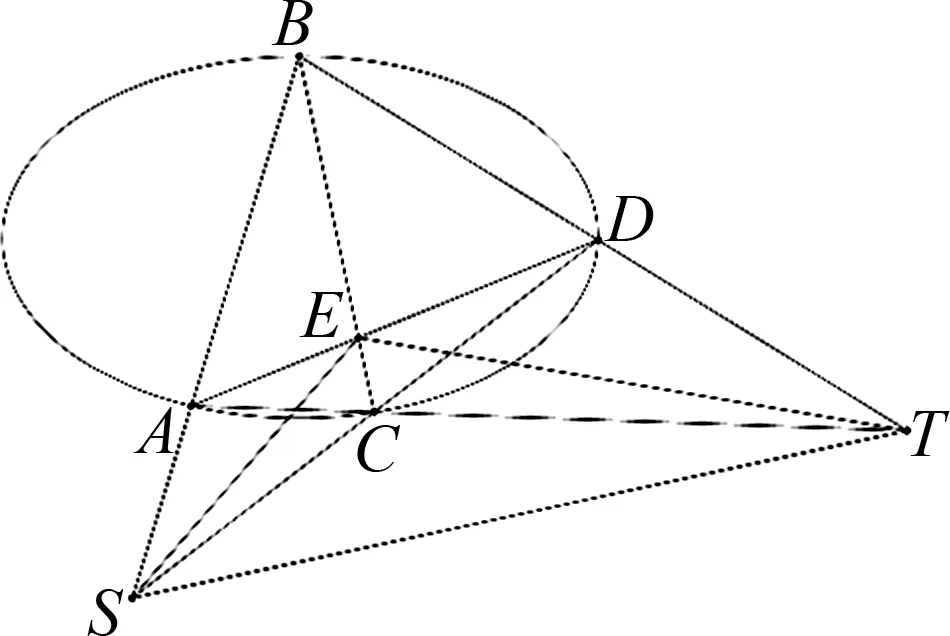
图1

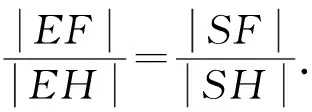
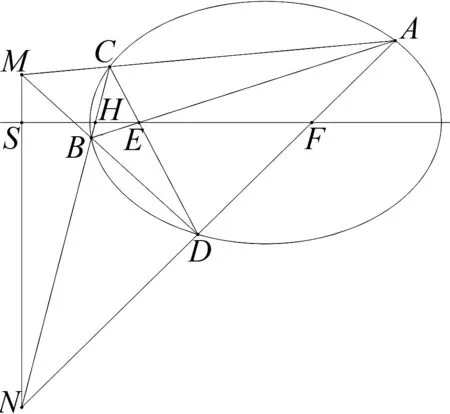
图2

例1 (2022高考数学全国卷甲卷理科改编)过抛物线y2=4x的焦点F的直线交抛物线于M,N两点，D(2,0)，MD交抛物线于另一点A，ND交抛物线于另一点B，设直线AB、直线MN的倾斜角分别为α,β，当α-β取最大值时，求直线AB的方程.

图3

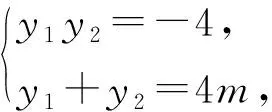
以高等几何中的极点与极线为背景命制的解析几何试题很多，认识这类问题有助于以高观点把握问题，将问题看得更为透彻，下面给出例1的两个变式.

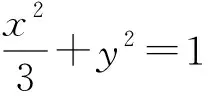
图4

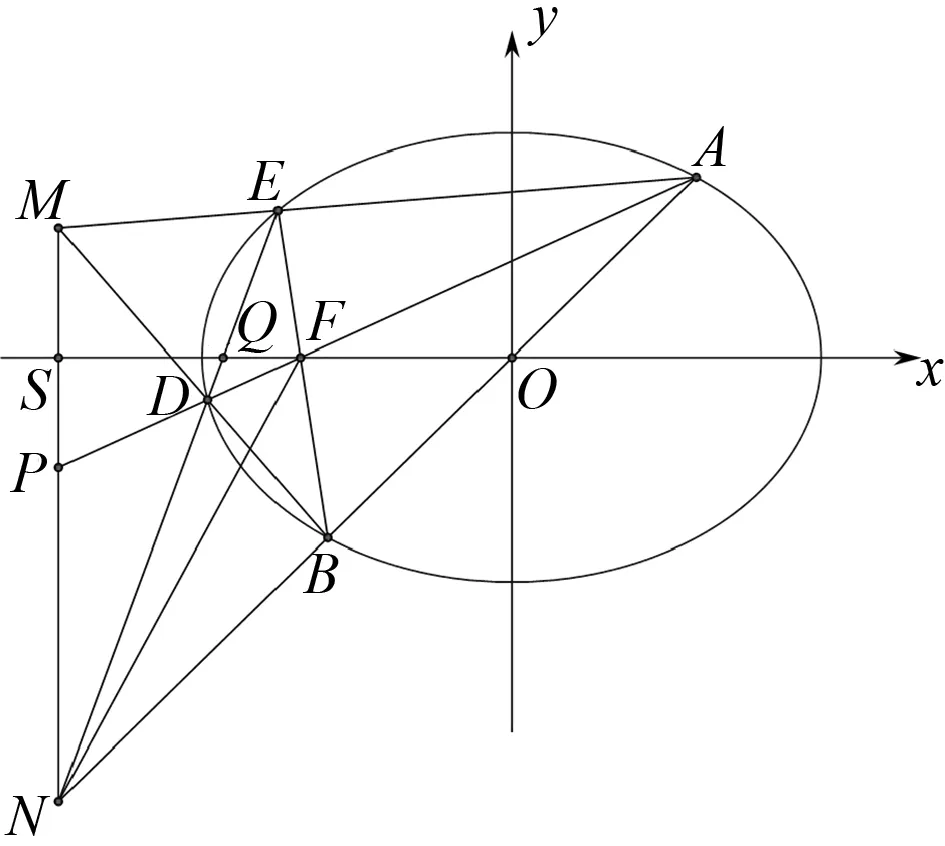
图5

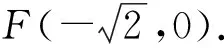
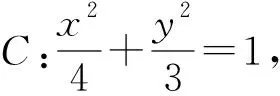
图6

图7

说明：变式2的结论与直线AB、直线A1B1的交点E在椭圆内、外无关，也与E在x轴的上方、下方无关.