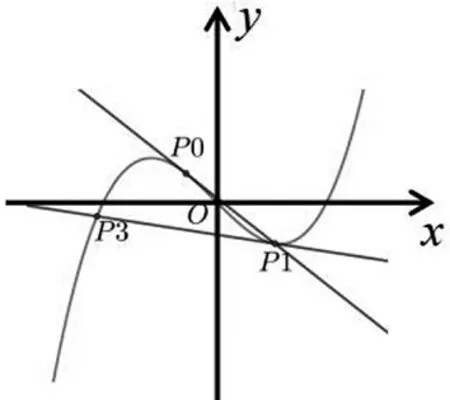
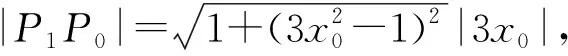三次函数的一个奇妙性质
浙江省江山中学 (324100) 徐丽峰
三次函数是高考、竞赛、强基等选拔性考试试题中的热点和难点,笔者在研究三次函数图像与直线的交点时,发现一个奇妙性质,利用该性质能极大的提高解题效率.本文呈现性质的发现与证明过程,并利用性质巧解高考题,妙解竞赛题.
一 性质的发现与证明
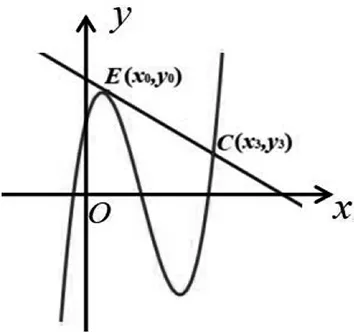
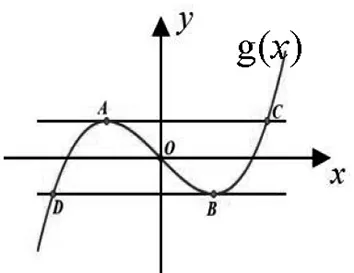
性质1 如图1,若曲线f(x)=ax3+bx2+cx+d(a≠0)的图像与直线y=kx+m交于不同三点,A(x1,y1),B(x2,y2),C(x3,y3)(x1 图1 图2 性质2为性质1的特殊情况,证明略. 图3 证明过程参考性质1. 性质的几何特征:三次曲线与直线相交或者相切. 性质的代数特征:存在不全相等的3个实数x1,x2,x3或1个实数x1,2个虚数x2,x3(本文主要研究前者),使得f(x1)-kx1=f(x2)-kx2=f(x3)-kx3=m(k,m为常数). 例1 (2021全国卷文乙21)已知函数f(x)=x3-x2+ax+1.(Ⅰ)讨论f(x)的单调性;(Ⅱ)求曲线y=f(x)过坐标原点的切线与曲线y=f(x)的公共点的坐标. 分析:题设中出现直线与三次函数图像相切的情形,这符合性质的几何特征. 例2 (2016年天津理科20)设函数f(x)=(x-1)3-ax-b,x∈R,其中a,b∈R.(Ⅰ)求f(x)的单调区间;(Ⅱ) 若f(x)存在极值点x0,且f(x1)=f(x0),其中x1≠x0,求证:x1+2x0=3; 分析:(Ⅱ) 中呈现性质的代数特征f(x1)=f(x0),其中性质中的k取0. (Ⅱ)如图4,由图像可知,x0是直线y=f(x0)与题中三次函数图像相切时,对应切点的横坐标点,x1是直线y=f(x0)与该曲线的另一个交点横坐标,由性质2或者用三次方程韦达定理易证. 图4 分析:若将题设中函数f(x)的零点问题转化曲线y=x3+bx与直线y=-c的图像的交点横坐标问题,这符合性质的几何形态. 图5 回顾近几年教师比赛、高中数学联赛、强基测试中的三次函数试题,发现这类试题均考察上述性质,以下笔者给出部分试题的分析. 例1 (2021年11月浙江省高中数学教师优质 课解题竞赛)已知三次函数f(x)=x3-x,设P0(x0,y0)为函数y=f(x)对应曲线C上异于对称中心的任意一点,在点P0处切线l0交曲线于P1点,在P1点处的切线l1交曲线于P2,求三角形P0P1P2面积(用x0表示) 图6 例2 (2019贵州预赛)设a,b,c是互不相等的实数, 多项式P(x)=x3+3x2+5x+7满足P(a)=b+c,P(b)=a+c,P(c)=a+b,则a+b+c=. 分析:P(a)+a=P(b)+b=P(c)+c(即性质中k取-1).令a+b+c=t,则P(a)=-a+t,P(b)=-b+t,P(c)=-c+t,故a,b,c均为曲线P(x)=x3+3x2+5x+7与直线y=-x+t交点的横坐标,由性质易得a+b+c=-3. 例3 (2021清华强基8)已知a,b,c是不全相等的实数且满足a=ab+c,b=bc+a,c=ac+b,则a+b+c=. 分析:题干为与a,b,c有关的三个三元二次方程,且为a,b,c轮换式,目标a+b+c也是轮换式,故考虑寻找a,b,c的同解三次方程,即a,b,c为三次曲线与直线y=0(即性质中k,m均取0)的交点的横坐标.采用消元的策略,最后化简得到c3-3c2+3=0,b3-3b2+3=0,a3-3a2+3=0,故a+b+c=3. 解题是我们老师最熟悉的动作,往年的考试真题则是我们的百宝箱.解题不能仅仅囿于问题的解决,而应在解题后,对高考题进一步观察、联想、探索,完成从一道题到一类题的转化.老师应当储备深厚的学科知识和敏锐的洞察力,甄选试题,寻找试题之间联系,揭示试题的规律,帮助学生更好理解数学,提高学习效率,将数学学习指向深处.


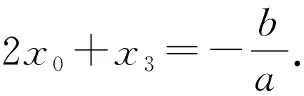


二 巧解高考题

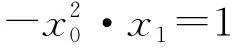



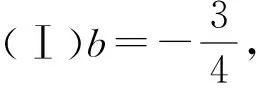
三 巧解竞赛题