始于教材 以生为本 聚焦思维*——一道函数导数压轴题命制历程

福建省厦门第一中学 (361003) 黄昌毅

《中国高考评价体系》指出，试题命制应以“一核、四层、四翼”为命题准则，试题考查内容以数学内容为主线，聚焦数学概念、定理、方法、思想的理解应用，试题注重数学本质，注重通性通法，试题突出基础性、综合性及创新性，试题难度适中，呈现“低起点、多层次、高落差”，突出试题的选拔功能[1].

笔者有幸参与了厦门市一次质检题的命制工作，对一道函数导数压轴题的命制历程，有较深感触，若有不足之处，敬请同仁批评指正.

1 试题再现

1.1 试题呈现

已知函数f(x)=2ax-ln(x+1)+1，a∈R.

(Ⅰ)讨论f(x)的单调性；

(Ⅱ)当x>0，0f(x).

1.2 试题简解

解：(Ⅰ)(略)；(Ⅱ)即证eax-2ax+ln(x+1)-1>0.

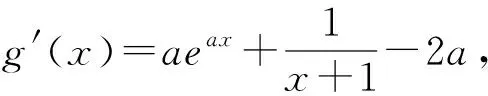
①当a=1时，h′(0)=0，则h′(x)>0，即h(x)在(0,+∞)上单调递增，则h(x)>h(0)=2-2=0；

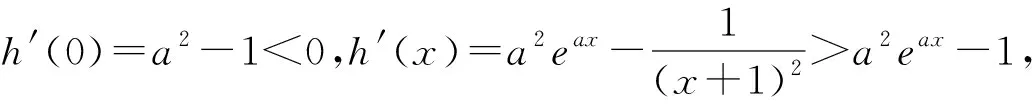
综上所述，h(x)≥0恒成立，即g(x)在(0,+∞)上单调递增，所以g(x)>g(0)=0，即eax>f(x).

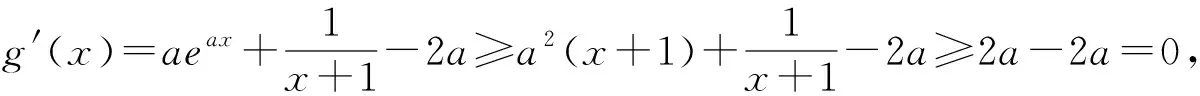
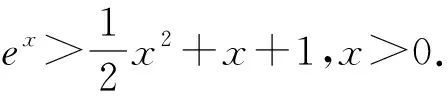
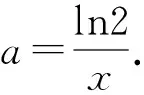
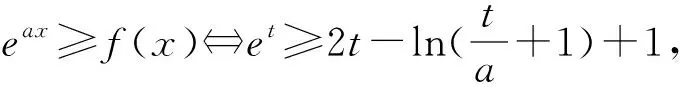
证法6：当x>0，00，下同证法5证明h(eax-1)>h(ax)即可.

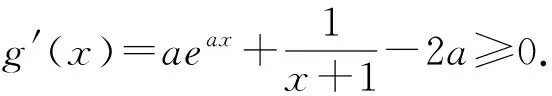
2 试题命制

2.1 审读要求 明确方向

认真研读命题要求，明确试题定位、命题依据及命题原则.命题细目表对第22题提出的3个要求：

(1)要求函数模型为指对函数混合模型，函数模型中含有参数函；

(2)试题共设置两小问，第(Ⅰ)问考查含参函数单调性的分类讨论，第(Ⅱ)问考查含参函数不等式证明，重点考查消元降次思想下的函数模型的优化意识；

(3)试题难度控制在0.25左右.

2.2 回归教材 寻求题根

高考(模拟)试题“源于教材”而又“高于教材”，教材是实现课程目标、实施教学的重要资源.教材的习题富有典型性和深刻性，因此要求教师要钻研教材，从教材中寻找试题的生长点，发挥教材的教育教学功能.

笔者多次翻阅教材，教材中的以下素材引起笔者的关注：

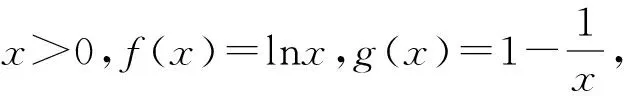
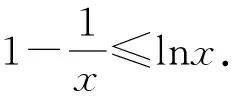
题3 (人教A版普通高中教科书数学选择性必修二P94练习2)证明不等式：x-1≥lnx，x∈(0,+∞).

题4 (人教A版普通高中教科书数学选择性必修二P99习题5.3题12)利用函数的单调性，证明下列不等式，并通过函数图象直观验证：

(1)ex>x+1，x≠0；(2)lnx0.[2]

题3、题4则给出了指数函数、对数函数与一次函数的大小关系：lnx≤x-1，x∈(0,+∞) ②；ex>x+1，x≠0 ③.

上述三个不等式可以进行相互转化：

教材中反复出现该不等式，同时这三个不等式也是高考考查的热点问题，故选定不等式ln(x+1)≤x作为命题的根源.

2.3 追踪热点 确定载体

高考试题是命题专家对教材的深度加工的智慧结晶，为此研究高考试题,发挥试题潜在的应用价值对备考复习具有导向功能, 因此参照高考试题命制模拟试题是明智之举.笔者翻阅近几年高考及各省市模拟考函数导数题，以下试题(节选)引起笔者注意：

题5 (2013年全国Ⅱ卷理科第21题)已知函数f(x)=ex-ln(x+m).当m≤2时，证明f(x)>0.

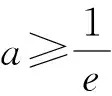
题8 (2020年高考卷第21题)已知函数f(x)=aex-1-lnx+lna.若f(x)≥1，求a的取值范围.

以上四题均以指对混合函数为模型，函数中含有参数a，最后证明双参不等式恒成立.试题均可通过主元思想消去变量a，化双变量为单变量；也可通过教材中出现的不等式ex≥x+1，lnx≤x-1及其常用变形进行放缩证明；还可通过研究函数导数的“隐零点”，采用“设而不求，整体代入”方法求解函数最值；也通过构造同构函数证明指对混合不等式.[3]

通过以上试题及相关材料分析，最终选定以下函数不等式作为模拟题的载体：

题9 证明：ex-2x+ln(x+1)-1>0，x∈(0,+∞).

分析：ex-2x+ln(x+1)-1>0⟺ex-(x+1)>x-ln(x+1)，易证明h(t)=et-t-1在(0,+∞)单调递增，且et≥t+1，t≥ln(t+1)，当x∈(0,+∞)时，x>ln(x+1)>0.则有h(x)>h(ln(x+1))，即ex-(x+1)>x-ln(x+1).

2.4 引入变量 初具雏形

题9难度中等，作为压轴题难度不够，命题明细表中明确要求考查含参函数不等式证明，故需要在题9的基础上适当添加参数:

题10 当x>0，00.

题11 当x>0，a≥1时，求证：ex-2x+ln(ax+1)-1>0.

题10、题11添加参数a，通过观察，很容易构造以a为主元的函数，利用主元法得到ex-2ax+ln(x+1)-1>ex-2x+ln(x+1)-1或ex-2x+ln(ax+1)-1>ex-2x+ln(x+1)-1.显然这样的参数引入，并不能增加试题的难度，因此，该题并不能达成预设目标，在上述基础上再次尝试改造：

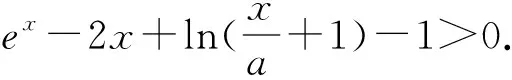
题13 当x>0，00.

结合题10、11改造出题12，虽本质上没有差别，但只需要在题12中将x用ax替换后则改造出题13.经过改造后，题13则无法直接利用主元法消去变量a,这样对函数模型进行适当包装，呈现形式较为新颖，但入口宽、解法较多且自然，不同能力层次的学生能有不同的解决方法，但思维量计算量有所区别，符合试题预设，因此试题初具雏形.

2.5 完善设问 终成定稿

确定函数不等式雏形后，根据试题本源和载体，需要设定最初函数模型，根据命题意图，还需设置试题第一问，故笔者设置以下完整试题：

题14 已知函数f(x)=2ax-ln(x+1)+1，a∈R.

(Ⅰ)讨论f(x)的单调性；

(Ⅱ)当x>0，0f(x).

题14给出的函数f(x)=2ax-ln(x+1)+1，函数模型学生较为熟悉，第(Ⅰ)问为简单的含参函数单调性讨论，考查学生分类讨论思想，符合命题细目要求.同时根据第(Ⅰ)问结论，可得φ(x)=x-ln(x+1)在(0,+∞)单调递增，从而当x∈(0,+∞)时，x>ln(x+1)，ex>x+1，为后续函数不等式证明提供基础,这样的设问方式将两小问联系在一起，前为后用，增强问题的关联性.

最后经过命题组成员讨论，对试题措辞进行精心打磨，最后确定题14为最终试题.

3 命题思考

3.1 源于教材 精雕细琢

教材是众多专家和一线教师集体智慧的结晶，教材是数学能力与思想的载体，蕴含着大量的“命题点”，许多高考试题就源于课本，它们是由课本的例题、习题进行变式、迁移、整合、扩展而成，同时教材内容又与高考试题有一定差距，因此教师要在全面、深度理解教材的基础上，善于用联系的观点探究课本习题和高考(模拟)试题的差异;善于在课本中寻找试题题根，探究试题与课本习题的结合点，在变化中发现不变的本质，再将这些进行拆分、整合、延伸、拓展，可能就是一道源自课本又高于课本，并且能充分展现学生思维能力的好题[4].同时试题考查的知识、方法要以教材为纲本，不宜考查超纲知识.

3.2 以生为本 聚焦思维

试题考查对象为学生，命题时应坚持以生为本.首先，应选择学生熟悉的素材作为载体，可从学生经常接触的生活事物、教材教参中选择命题素材；其次，命题要注意语言表述，试题语言在规范准确的前提下要力求简洁，便于学生理解；最后，命题时要关注学生知识与能力的最近发展区，不宜出特别难或复杂的问题，不人为设计陷阱.

数学是思维的体操，缺少思维量的试题不是一道好题，命题不宜照搬旧题，试题要一定的新颖性，这样才能激发学生兴趣，调动学生积极性，引发学生思考，鼓励学生创造性思维；试题不宜偏、怪、烦，这样让学生主动放弃思考，也达不到试题考查目的.

3.3 一题多解 突出选拔

学生在数学概念的理解、基本数学方法的掌握，数学素养的养成等方面与思维水平有高度的关联性，因此在试题的命制的过程中重视难度和思维的层次性，给广大学生更广阔的思考空间，更多的思考角度，以及基于自己认知水平的发现和探索解题方法的不同平台.因此在试题的难度设计上不仅有层次性，而且要在思维的灵活性、深刻性，方法的综合性、探究性和创造性等方面，科学把握试题的区分度，全面体现数学科高考的选拔性功能.一道好的试题，一定要体现解题方法的多样性，给不同层次的考生提供多种分析问题和解决问题的途径是，在思维能力上、在解题方法上体现试题的选拔功能.

试题命制，功在平时.教师在平常教学中对试题深度剖析、挖掘本质、追根溯源.要深化对问题本质的理解，要熟读教材教参，不断尝试对教材例题、习题等内容改编、整合，在平时命题尝试中不断总结经验，完善认知，形成素养内化于心，才能厚积薄发.