一道数学联赛预赛题的解法探究

广东省深圳中学 (518001) 邱际春

2019年全国高中数学联赛广西省预赛第11题是一道平面几何试题：

题目如图1所示，AD、AH分别是△ABC(其中AB>AC)的角平分线、高线，点M是AD的中点，△MDH的外接圆交CM于点E.求证：∠AEB=90°.

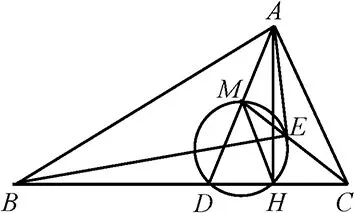
图1

此题的主要构形为三角形与圆，涉及圆内接四边形、角平分线及四点共圆的有关性质.文[1]利用相似和到角给出了证明.笔者观察图形的结构特征，结合平面几何中的常用定理及几何变换，从多个视角给出下面几种不同的证明方法.

视角一 利用角平分线、高线的性质，结合倒角和相似转化

图2

评注：注意到几何图形中多对相似三角形，通过证明三角形相似可以得到角的关系，进而利用到角来证明该命题便水到渠成.

视角二 借助中线长公式、勾股定理，寻找线段之间的关系

图3

评注：考虑到在几何图形中包含中线及多个线段的垂直关系，故可尝试利用中线长公式和勾股定理来寻找对应边之间的关系，从而证明三角形相似，进而利用倒角来证明所证结论.

视角三 巧妙构造外接圆，运用圆的有关性质转化

证法3：如图4，连接DE，作△CDE的外接圆⊙O，连接并延长EH交⊙O于点F，连接CF、DF，则因为∠MHD=∠MED=∠CFD，∠MDH=∠CEF=∠CDF，所以△CDF～△MDH.又△MDH是等腰三角形，所以△CDF是等腰三角形，所以CD=CF，∠CDF=∠CFD=∠MDH，所以AD切⊙O于点D.由切割线定理知MD2=ME·MC，又AM=MD，所以AM2=ME·MC，所以△EMA～△AMC，所以∠MEA=∠MAC=∠BAD，所以∠MEA+∠MAE=∠BAD+∠MAE=∠BAE，所以∠AME=180°-∠MEA-∠MAE=180°-∠BAE，又∠BHE=∠AME，所以∠BHE+∠BAE=180°，所以A、B、H、E四点共圆.故∠AEB=∠AHB=90°，命题得证.

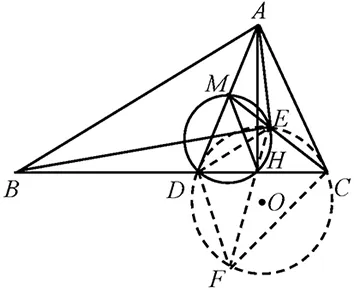
图4

评注：上述几何图形中存在多组相似三角形，而证明三角形相似的途径有很多.考虑圆内接四边形的性质，可通过构造出另一圆内接四边形，利用切割线定理得到比例线段，进而证得三角形相似，从而倒角即可完成证明.

视角四 利用反演变换的保角性，使其化繁为简

证法4：如图5，以A为反演中心，单位长度为反演半径作反演变换.于是∠B′AD′=∠D′AC′,AD′=D′M′，直线BC的反形为以AH′为直径的圆，要证∠AEB=90°，只需证∠AB′E′=90°.设D′H′,M′E′,AC′交于三圆根心K，则KD′⊥AD′，又AD′=D′M′，所以AK=KM′，从而∠B′H′D′=∠B′AD′=∠C′AD′=∠AM′K=∠180°-∠D′H′E，于是B′、H′、E′三点共线，故∠AB′E′=∠AB′H′=90°.因此∠AEB=90°，命题得证.

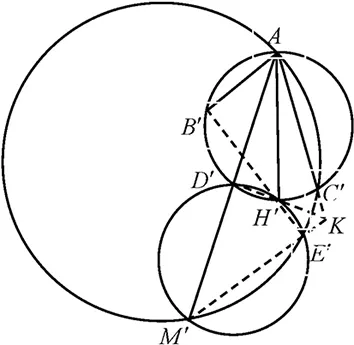
图5

评注：由于反演变换作为一种几何变换具有互逆性、保角性等独特的性质，常用来证明线段、角等几何量之间的关系.

结语：通过对上述预赛试题的剖析，我们从不同角度来解决这一图形优美、结构简练的几何赛题，进而得到了多种不同方法.由此可以看出，这是一道选拔考生和锻炼学生发散性思维的绝好素材.每年世界各地的奥赛试题层出不穷、浩如烟海，且不乏构思精巧的试题.如果能对赛题深度分析，做到一题多解，将有助于培养创造性思维能力，从而提高解题能力.