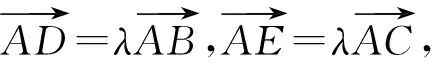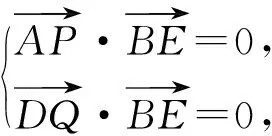一道北大综合营试题的证法赏析

江苏省南通市海门四甲中学 (226100) 沈佳瑶

近年，北京大学每年暑期都会举办数学体验营活动.这类活动的题目总体难度不大，但有竞赛的味道.2019年北大综合营第4题是一道平面几何题，笔者探究出这道试题的多种证法.

一、试题呈现

如图1，已知等腰直角△ABC，∠A=90°，点D在边AB上，E在边AC上，AD=AE，过点A,D分别作BE的垂线交BC于P,Q.用平面几何方法证明：PQ=PC.

图1

试题简洁明了，结构也不算复杂，题目特意强调用平面几何方法证明.自然的想法就是添加辅助线，证明的途径较多，关键在于利用题目条件进行合理的转化.

二、证法赏析

思路一两条线段AP和DQ都垂直于BE，可以通过构造平行线成比例解决问题.不同的解题视角，可得到以下4种证法.

证法1：如图2所示，构造一个正方形ABFC，延长AP、DQ交CF于是点S、点R.由于AP⊥BE，DQ⊥BE，则AS//DR，又AD//SR，所以四边形ADRS为平行四边形，所以AD=RS.由条件知Rt△BAE≌Rt△ACS，则AE=CS，又因为AD=AE，所以CS=SR，结合PS//QR，得PQ=PC.

图2

证法2：如图3，延长DA至点F，使得DA=AF，连接CF.由条件可知Rt△BAE≌Rt△CAF，则∠AEB=∠AFC，AE=AF.由DQ⊥BE，知∠BDQ=∠AEB=∠AFC，所以CF//DQ，又因为DA=AF，故PQ=PC.

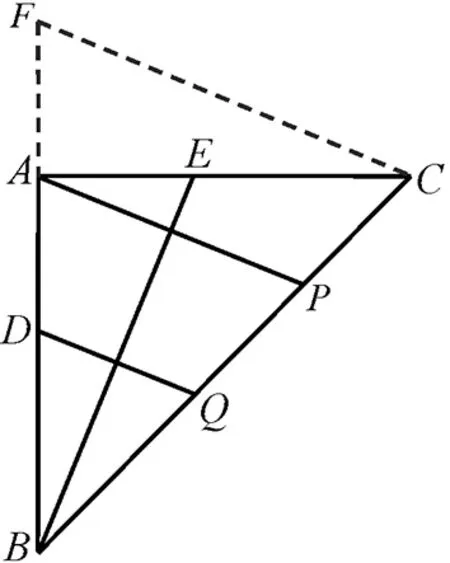
图3

证法3：如图3所示，延长DA至点F，使得DA=AF，连接CF.因为AD=AE，所以AE=AF.由条件可得△ABE≌△ACF.所以∠AEB=∠AFC.所以∠ABE+∠AFC=∠ABE+∠AEB=90°.所以FC⊥BE，从而FC//AP//DQ.又因为DA=AF，所以CP=PQ.

证法4：如图4所示，过点C作CF//AP交BA的延长线于F点，延长BE交FC于点H，设DQ交BE于G点，AP交BE于I点.连接AH和AG.因为AE=AD,AC=AB，所以CE=BD.由DQ⊥BE，∠A=90°，得∠BDG=∠BEA=∠CEH，所以Rt△BGD≌Rt△CHE，所以DG=EH.由∠BDG=∠CEH，得∠ADG=∠AEH，所以△ADG≌△AEH，所以AG=AH,AG⊥AH，因为AI⊥GH，所以GI=IH.又因为DQ//AP//FC，所以CP=PQ.

思路二图形中有众多垂直关系，可以通过作垂线，构造全等三角形和相似三角形，可得以下两种证法.

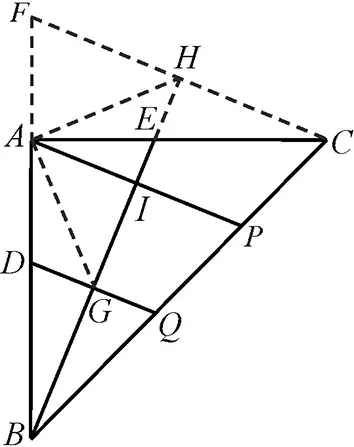
图4

图5

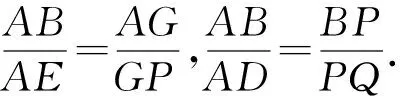
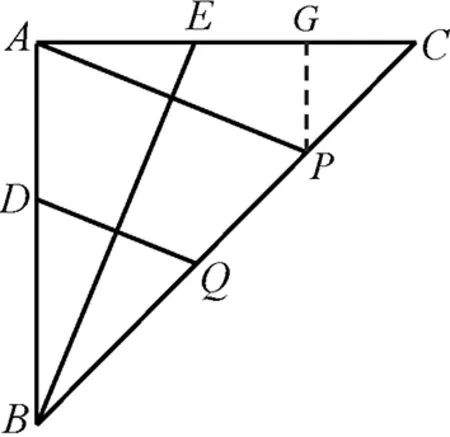
图6

思路三利用旋转变换，同样可得全等三角形，这样两个三角形对应边互相垂直，且梯形的中位线与上、下底都是平行的.可得以下证法.

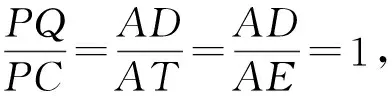
图7

思路四题目即是证明点P是线段CQ的中点，可以联想三角形中位线.得到以下证法.

证法8：如图8所示，连接CD交AP于F点.由条件知AP⊥BE，DQ⊥AE，△ABE≌△ACD，所以∠ADC=∠AEB，∠ABE=∠ACD，又∠AEB+∠ABE=∠AEB+∠CAP=90°，所以∠CAP=∠ABE=∠ACD，所以FA=FC.又∠ADC=90°-∠ACD=90°-∠CAP=∠DAF，所以FD=FA，所以FD=FC.因为AP//DQ，所以CP=PQ.

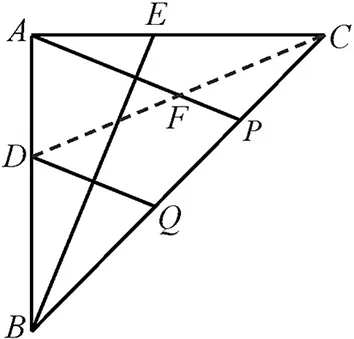
图8

思路五直观的证明难点在于点P、点Q的表达，利用面积可以实现消点.得到如下证法.

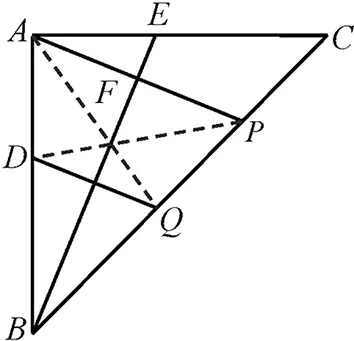
图9

思路六既然是证法赏析，我们抛开题目限定的平面几何方法去思考其他的方法，我们又可得到三角法和向量法两种典型的证明方法.

图10