例谈数形结合在求解三角形最值问题中的妙用

安徽省巢湖市第四中学 (238000) 车承梅

解三角形中经常会出现求最值或范围类的问题，此类问题有时难度相对较大，有一定的运算量，但是我们可以试着从几何图形的直观性入手，借助于平面几何的知识，将代数问题转化为几何问题去解决，这样可以大大减少计算量，从而达到事半功倍的效果.下面将通过几个实例去探究数形结合在求解三角形的最值(或范围)问题中的妙用.

例1 △ABC中，内角A，B，C所对的边分别为a，b，c，且(sinA-sinC)2=sin2B-sinAsinC，b=3，则△ABC的面积的最大值为.

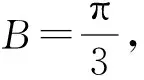
图1

评注：此题的条件属于边角对应型的，于是联想到圆的性质，即同一条弧所对的圆周角相等，这样就知道了点B的活动范围，从而使问题迎刃而解.

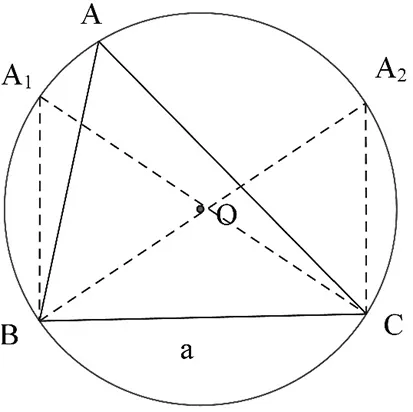
图2

由条件可知，点A在优弧BC上运动(不与B,C重合)，当AB⊥BC时，△ABC为直角三角形(图中为△A1BC)，此时b最大，c最小，且b=4，c=2，所以b-c=2；当AC⊥BC时，△ABC也为直角三角形(图中为△A2BC)，此时b最小，c最大，且b=2，c=4，所以b-c=-2，当点A在点A1与点A2之间时，△ABC为锐角三角形，所以b-c∈(-2,2).

评注：本例与实例1相似，条件都属于边角对应型，此类问题都可以借助于三角形的外接圆来解决.

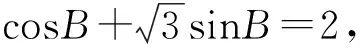
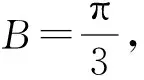
图3

评注：此题为边角不对应型，根据条件找到点C的活动范围，从而观察出使△ABC为锐角三角形的位置.

例4 在△ABC中，内角A，B，C的对边分别为a，b，c，已知a+b=8，2sin(A+B)=sinA+sinB，则△ABC面积的取值范围为.

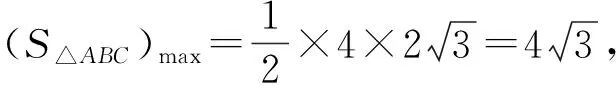
图4

评注：焦点三角形是椭圆中的一个重要三角形，有很多性质可以利用，而本题通过a+b=8联想到椭圆的定义，从而利用焦点三角形的性质轻松的解决了问题，可谓“妙极”.

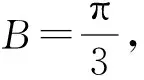
图5

评注：此题利用中位线的性质，将△ABC的面积转化为△BDE的面积，使之成为与实例1的相同的情形.其实，本题还可以进行扩展，当点D在线段AC上任意分点位置，都可以作平行线，从而利用相似性转化为实例1的情形去解决，这也是我们常说的“解一题而通一类”.